近地轨道电磁编队飞行相对轨道动力学建模

侯振东，曹喜滨，张锦绣

(哈尔滨工业大学 卫星技术研究所，150080 哈尔滨，hzd1988120@126.com)

卫星编队飞行技术是近几年提出的空间科学领域的新技术，具备系统成本低、性能好、可靠性高和适应性强等优点.但由于地球扁率、大气阻力等影响，通常需要附加作用力与力矩对成员卫星的相对位置与姿态进行控制.传统采用的喷气推进由于能量消耗，影响编队飞行寿命，且推力器排出的羽流可能污染邻近卫星的光学器件表面.而电磁编队飞行(EMFF)利用通电线圈产生的电磁力来实现编队构型的保持与控制，并由太阳能提供机动能量，且不存在羽流污染，在编队飞行中将会有很大的应用前景.

自电磁编队飞行的概念提出以来，国内外学者进行了先期探索和研究，取得了部分成果.其中，Schweighart［1］提出了近场、中场和远场三种电磁力模型.Hashimoto［2］与Kaneda［3］等分析了低地球轨道(LEO)的电磁编队飞行动力学模型，并对在同一平面运行的相对距离固定的双星系统进行了详细分析.Elias［4］提出了电磁编队飞行的通用非线性动力学模型，对卫星星体、飞轮、电磁体以及飞轮和星体的连接部分都建立了数学模型.Elias［5］还研究了稳定旋转的双星系统动力学，该双星系统绕其质心旋转，同时径向距离保持恒定，维持这种运动的径向力由电磁力提供，在论述中作者将非线性动力学模型在理想轨迹附近线性化，并进行了稳定性分析.

本文假设编队系统中每颗卫星都安装3 个正交的通电线圈，通过改变每个线圈的电流大小、方向，可产生任意大小、方向的电磁控制力与力矩，实现编队构型的保持与控制.另外星体上还安装3 个正交的飞轮，用来控制星体姿态.产生电磁体的激励电流和飞轮旋转所需的能源由太阳帆板提供.本文在此基础上，考虑大气摄动、地球扁率J2摄动，建立电磁编队飞行的非线性相对轨道动力学模型，并对相对轨道动力学方程进行线性化，得到参考坐标系下的线性化相对轨道动力学方程.

1 坐标系定义

为叙述方便，建立以下4 种直角坐标系.坐标系示意图见图1.

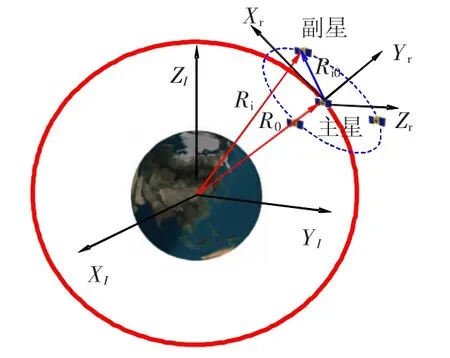
图1 坐标系定义

地心惯性坐标系FI:原点在地心Oe;XI轴指向赤道平面与黄道平面相交接线的升交点(即春分点);地球自转轴为ZI;选择YI使其与XI、ZI满足右手坐标.

主星参考坐标系Fr:原点在主星质心Or;Yr轴沿地心与主星的连线方向，指向主星;Xr轴指向主星速度方向;Zr轴与Xr、Yr构成右手坐标系，指向轨道面负法线方向.

卫星轨道坐标系Fo:原点在卫星质心Oo，各轴指向类似于主星参考坐标系，只不过卫星轨道坐标系针对的是相应的卫星，而非主星.

线圈安装坐标系Fm:原点在卫星质心Om(即Oo);Xm、Ym、Zm三轴分别沿星上3 个正交的通电线圈平面的法线方向.

为叙述方便，记编队卫星数目为n，编号依次为0，1，2…，n-1，其中卫星0 为主星.

2 任意两星间电磁力建模

电磁编队飞行的电磁力由卫星上的通电线圈产生.如果用fij表示卫星B 上第j 个线圈产生的磁场对卫星A 上第i 个线圈的作用力，则两颗卫星间的电磁力为

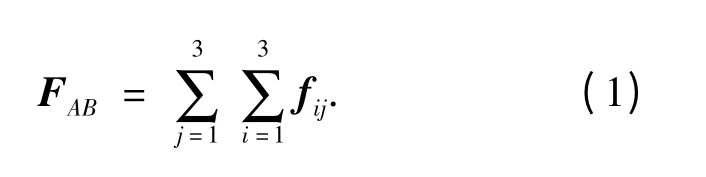
参照文献［1］，建立远场模型.以任意两颗卫星i 和j 为例，记μi为卫星i 的磁偶极子矢量，μj为卫星j 的磁偶极子矢量，μ0为真空磁导率，Rij=Rj-Ri为两颗卫星的相对矢径，Rij为相应距离.则卫星j 对卫星i 的电磁力与电磁力矩分别为

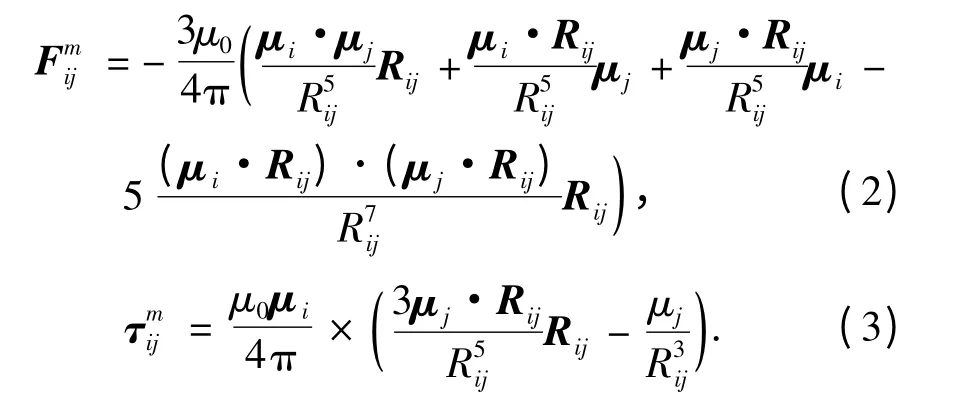
为便于分析，假设以反作用飞轮完成卫星的姿态控制，在建模过程中暂不考虑电磁力矩对相对轨道运动的影响.

式(2)中，μi在安装坐标系下可表述为

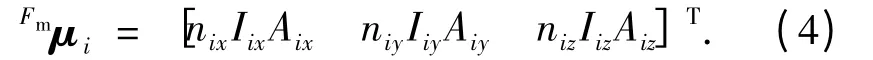
式中:nix表示安装坐标系Xm轴的线圈匝数;Iix表示Xm轴的电流强度;Aix表示Xm轴的线圈所围面积;Fm表示分量所在坐标系，其他符号的意义依此类推.

采用zxy 顺序的欧拉角转换形式，卫星i 的轨道坐标系到安装坐标系的坐标转换矩阵为

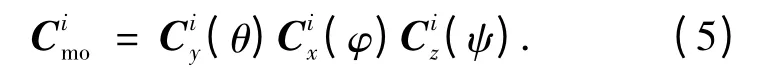
采用zxz 顺序的欧拉角变换，地心惯性坐标系到卫星i 的轨道坐标系的坐标转换矩阵为

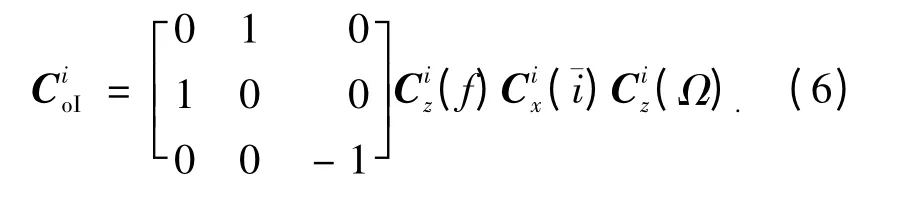
式中Ω 为卫星的升交点赤经，¯i 为轨道倾角，f 为纬度幅角.

由参考坐标系的定义可知，地心惯性坐标系到主星参考坐标系的转换矩阵与式(6)相似.

由公式(5)、(6)可得μi在地心惯性坐标系下的表达式为

式中μj在地心惯性坐标系下的表述与μi类似.将公式(5)～(7)代入式(2)，可得卫星j 对卫星i 的电磁力在地心惯性坐标系下的分量形式，将作为仿真程序的理论基础.

由式(2)～(7)可见，两颗卫星间的电磁力与两星的磁偶极子相耦合，与相对距离的四次方成反比，具有强烈的非线性.而磁偶极子是两颗卫星姿态及线圈电流的函数(一般情况下线圈匝数与所围面积是常数).结合电磁力产生的机理与公式分析可知，任意两星间的电磁力是两星相对位置、相对姿态及各线圈电流的1 个非线性函数.

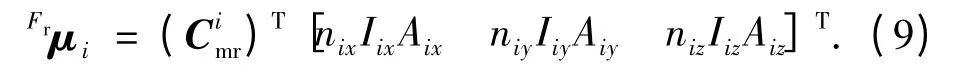
同理，将式(9)代入式(2)中，可得卫星j 对卫星i 的电磁力在主星参考坐标系下的分量形式.

理论上编队卫星所受的电磁力应包括地磁场的作用.但由参考文献［6］可知，在轨道高度不低于200 km，编队距离几十米的情况下，地磁场对卫星的电磁力至少比两星相互作用的电磁力小1 个数量级，因此在电磁力建模时可以忽略地磁场对卫星的影响.

3 线性化相对轨道动力学模型建立

相对轨道动力学方程建立在参考坐标系下.参照希尔方程，可得卫星i 的相对轨道动力学方程为

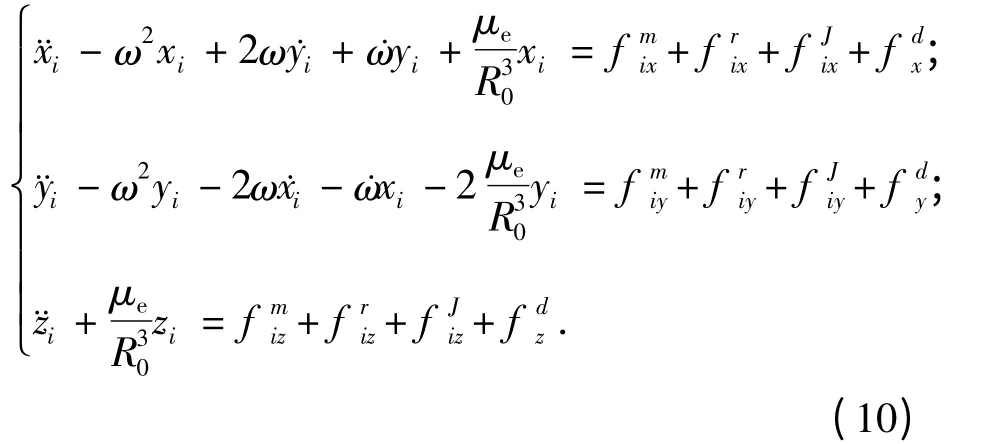
式中:ω 为主星轨道角速度;μe为引力常数;m 为卫星质量;R0为主星地心距;且

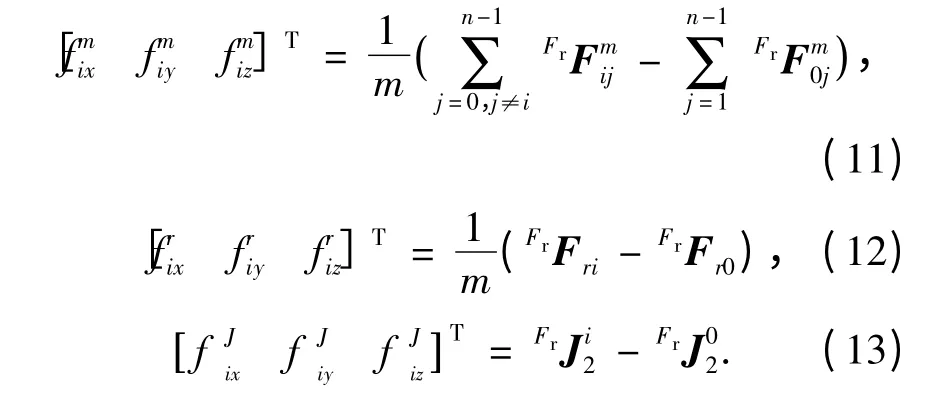
3.1 电磁力线性化

在多颗卫星(多于两颗)的电磁编队飞行中，每两颗卫星之间都会产生电磁力.多颗卫星编队的电磁力实质上是任意两颗卫星间电磁力的叠加.为方便起见，本文先研究双星编队系统，两颗卫星标号为i、j.由坐标系定义可知，卫星0 为主星.这里以卫星i 为主星来分析卫星i、j 之间的电磁力线性化方法.由于卫星姿态由飞轮协同控制，理论上可将卫星姿态稳定在任意方位.为方便讨论，假设在飞轮作用下，各卫星的线圈安装坐标系与主星参考坐标系指向重合.在参考坐标系下记Rij=［x y z］T.由式(9)可得:

由式(14)、(15)及式(2)可得到在上述假设条件下的电磁力表达式为

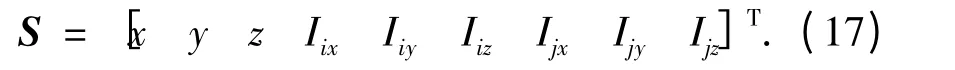
利用泰勒定理对Fmij在理想点

展开得

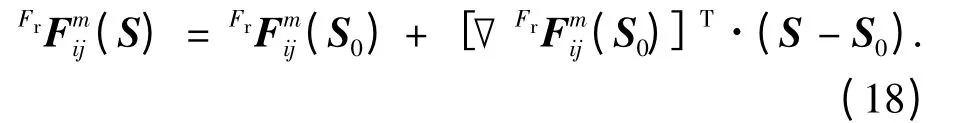
由式(19)可知，根据某一理想点S0可求出任意S 处的电磁力，电磁力简化为S 的线性函数.但这一表述基于泰勒展开定理，舍去二阶以上表达式，只在S-S0较小时精确成立.因此为达到精度要求，实际应用中需要实时校正理想点S0.

下面推导n 颗卫星相互作用时电磁力的线性化.先假定有多颗主星，表述时以卫星i为主星，按上述方法可表述如下:

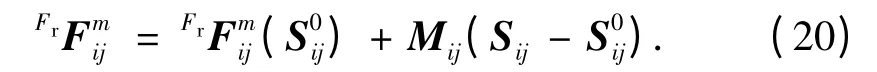
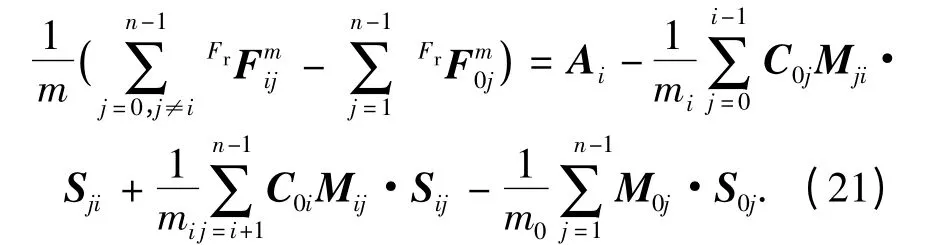
记

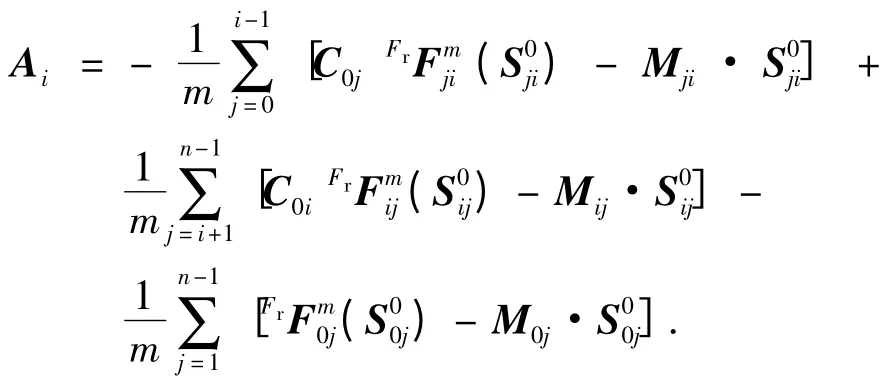
为线性化的常数项.

由式(21)可知，多颗卫星的电磁编队飞行中电磁力的线性化表述还有坐标转换矩阵的影响，增加了电磁力表达式的耦合性.这是由电磁力的作用机理决定的，给实际应用带来困难.对于多星电磁编队飞行的电磁力线性化，本文只做初步的分析总结.

3.2 气动力线性化

假设n 颗卫星气动参数的CD和密度ρ 均相同，有一定的面质比偏差.记主星迎流面面积为A，卫星i 迎流面面积为A+δA.则卫星i 的气动阻力在主星参考坐标系下表述为

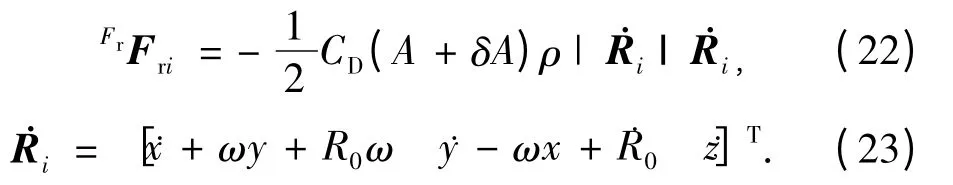
分别对式(22)中的［˙x ˙y ˙z］T、［x y z］T、δA求梯度，可导出

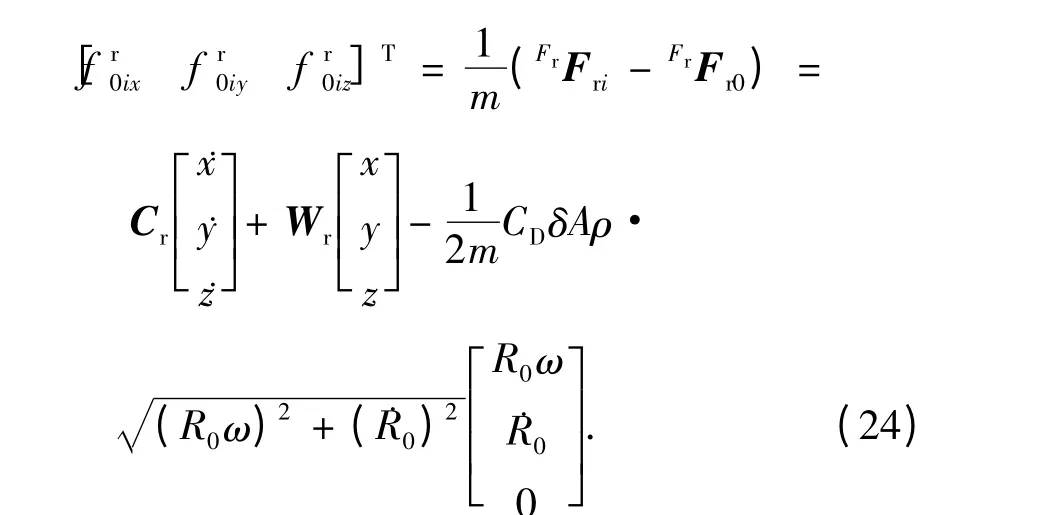
其中:

3.3 J2 摄动线性化

结合本文的坐标系定义，对参考文献［7］的公式略作修改，可得

式中:

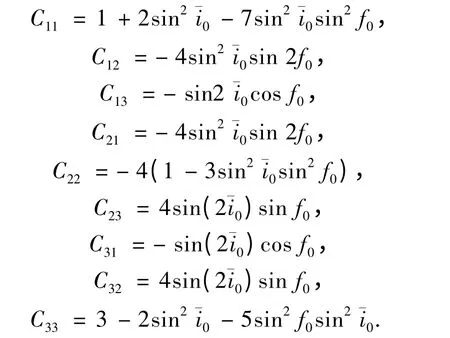
3.4 相对轨道动力学方程最终表述

略去未知干扰项，由式(10)～(25)可得卫星i 在主星参考坐标系下的线性化相对轨道动力学方程为

其中:

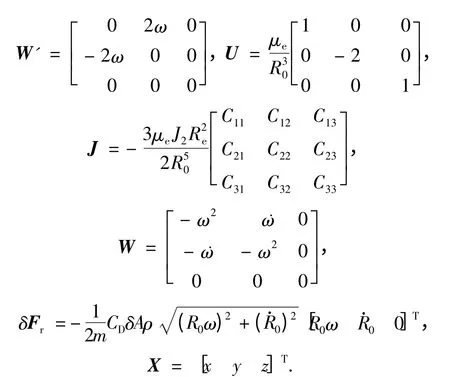
针对两颗卫星的电磁编队飞行，略去未知干扰因素，公式可简化为

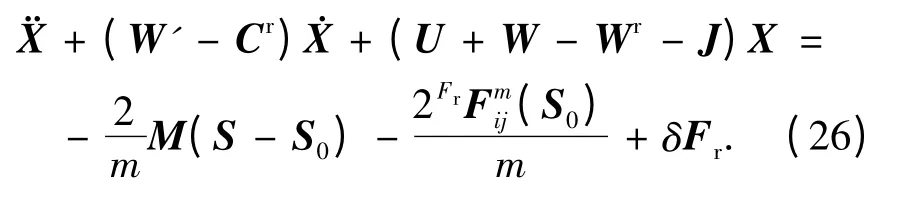
式(26)是相对位置［x y z］T及控制量［IixIiyIizIjxIjyIjz］T的线性微分方程组，对控制算法设计及其他理论分析带来便利.

经分析，式(26)还可整理为状态空间的表达形式.选状态变量为控制量I =［IixIiyIizIjxIjyIjz］T.式(26)的状态空间描述如下:

其中:

式中:E 为3×3 阶单位矩阵;M1M2为矩阵-2M/m 的子式，且-2M/m=［M1M2］，M1为3×3 阶矩阵，M2为3×6 阶矩阵;F 为常数向量.

4 仿真及结果分析

为考核线性化相对动力学模型的可用性及精度，对线性化相对轨道动力学模型与未线性化轨道动力学模型分别进行仿真分析.仿真中设定主星与从星各轴线圈匝数、所围面积相同.大气密度查表可得.表1 给出初始时刻两颗卫星的轨道参数.两颗卫星的其他设计参数见表2.轨道参数的选择以构成串行编队为约束，卫星间距约为20 m.不失一般性，从星的三轴电流均设为I =I0+δI=［2000+100sin(πt)］A，主星的三轴电流均设为I0=2 000 A.

表1 卫星轨道参数

表2 卫星其他设计参数

在上述条件下对线性化与非线性的动力学模型进行仿真，电磁力线性模型与非线性模型的变化曲线见图2.线性模型与非线性模型的运动情况见图3.

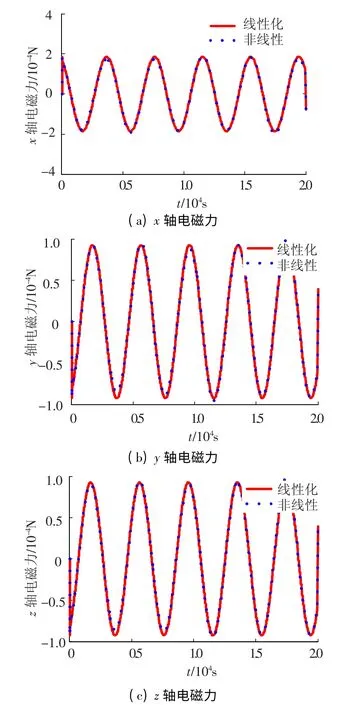
图2 电磁编队线性模型与非线性模型的电磁力对比

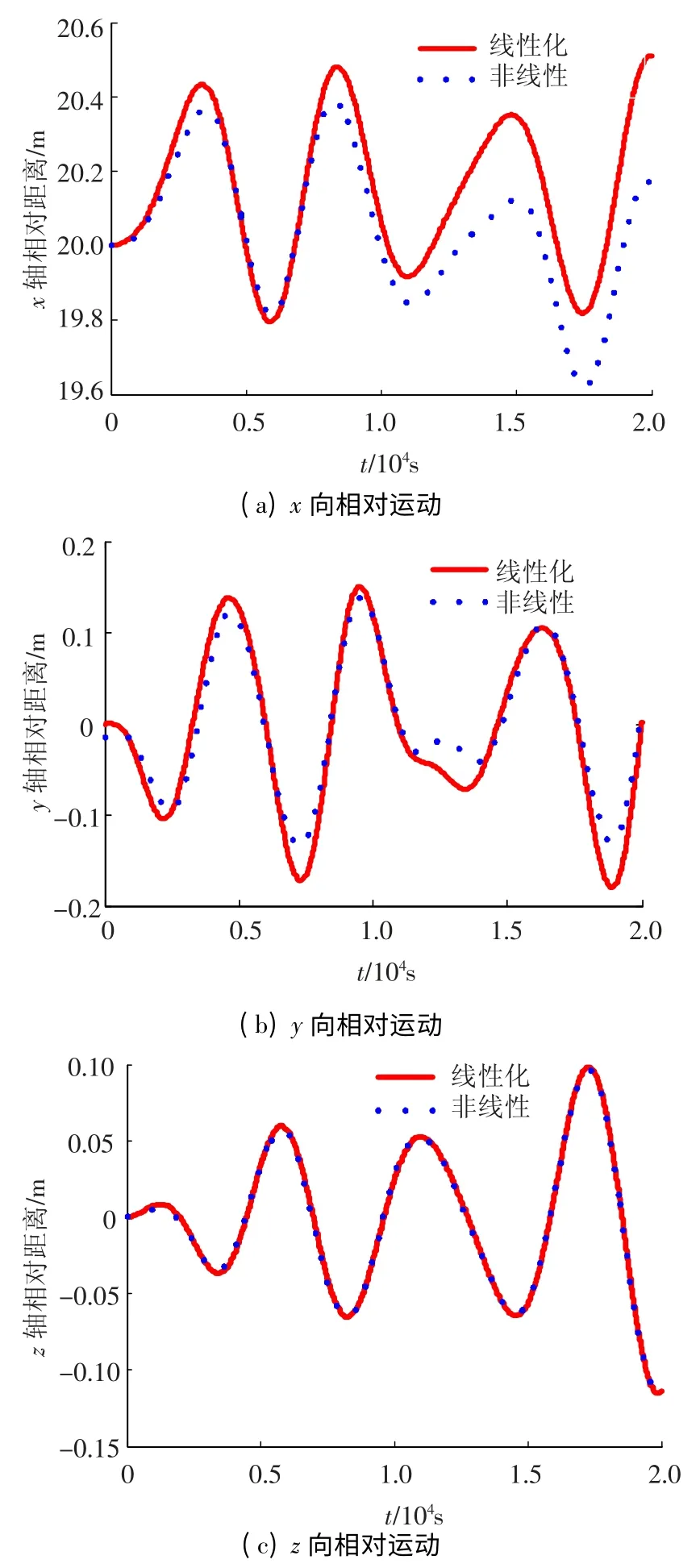
图3 电磁编队线性模型与非线性模型精度对比

由图2 可见，在20 000 s 的仿真时间内，电磁力线性模型与非线性模型计算值几乎一致，误差不超过10%，说明电磁力线性化是合理的.

由图3 可见，在20 000 s 的仿真时间(卫星轨道周期约5 900 s，即卫星运行3 个周期多)内，线性模型与非线性模型运行轨迹几乎重合，线性模型与非线性模型的主从星相对运动在主星参考坐标系的y、z 两轴误差不会发散，x 轴误差逐渐发散，在仿真结束时有0.3 m 的误差.单独分析电磁力、J2摄动等每一项单独作用力线性化对模型精度的影响.仿真结束时，电磁力线性化可使模型误差达0.2 m，其他作用(气动阻力线性化、J2摄动线性化及Hill 方程误差)对模型精度影响不超过0.1 m.

为考察不同轨道高度与不同卫星质量对模型精度的影响，设置轨道高度分别为6 600 km、6 882 km、7 400 km，卫星质量分别为100 kg、300 kg、500 kg，做9 组仿真实验.鉴于x 轴误差为主要误差，图4 给出各种情况下的线性化模型与非线性模型的x 轴误差.由图4 可见，误差随卫星质量的减小而增大，这是因为在一定的电磁力线性化误差下，小质量卫星受到的电磁加速度误差更大.减小线圈电流可以减小轻质量引起的误差.图4 还表明轨道越高，误差越小.分析认为高轨道卫星受大气阻力、J2摄动的影响较小，电磁力对相对位置的影响变大，使得模型对电磁力线性化的误差更为敏感.

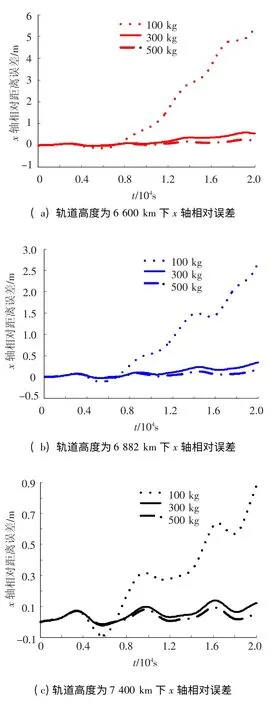
图4 不同轨道高度与卫星质量情况下的x 轴误差

仿真结果还表明这9 组实验中x 轴误差主要由电磁力线性化产生，但篇幅有限，没有列出仿真图.

综上所述，本文建立的电磁编队线性化轨道动力学模型在低轨道(200 ～1 000 km)、小卫星(100 ～500 kg)、编队距离20 m 左右、激励电流几千安的条件下是合理的，仿真结束时误差在0.05 ～5 m 范围内.且误差主要来自于电磁力线性化.为电磁编队飞行动力学的进一步研究提供参考，也可作为控制研究的理论基础.

5 结 论

本文以基于磁偶极子假设的远场模型为基础，在考虑大气摄动、地球扁率J2摄动的条件下推导了电磁编队飞行的非线性相对轨道动力学模型，并在一定条件下，对动力学方程线性化，最终得到基于Hill 方程的线性化相对轨道动力学方程.利用Matlab/Simulink 对电磁编队线性模型与非线性模型进行建模仿真，结果表明本文建立的线性化相对轨道动力学与精确的非线性模型很好吻合，x 轴相对运动有累积误差，误差主要源于电磁力线性化，且误差在一定的运行时间内很小.

由本文分析可知，线性化模型结构清晰，形式简单，便于独立分析各控制变量作用，有利于更成熟的线性控制方法的应用.非线性模型精度高，但结构复杂，控制算法设计上有困难.本文的线性化模型合理可行，结果将为电磁编队飞行的控制研究奠定理论基础.

［1］SCHWEIGHART S A，SEDWICK R J.Propellantless formation flight operations using electromagnetic formation flight［C］//SpaceOps 2006 Conference.Rome，Italy:［s.n.］，2006:1-38.

［2］HASHIMOTO T，SAKAI S，NINOMIYA K，et al.Formation flight using super-conducting magnets［C］//International Symposium of Formation Flying Missions and Technologies.Toulouse，France:［s.n.］，2002:3-10.

［3］KANEDA R，YAZAKI F，SAKAI S，et al.The relative position control in formation flying satellites using superconducting magnets［C］//2nd International Symposium on Formation Flying Missions and Technologies.Washington，DC:［s.n.］，2004:3-5.

［4］ELIAS L M.Dynamics of multi-body space interferometers including reaction wheel gyroscopic stiffening effects:structurally connected and electromagnetic formation flying architectures［D］.Combridge，MA:Massachusetts Institute of Technology，2004:1-23.

［5］ELIAS L M，KWON D W，SEDWICK R J，et al.Electromagnetic formation flight dynamics including reaction wheel gyroscopic stiffening effects［J］.Journal of Guidance，Control，and Dynamics，2007，30(2):499-511.

［6］AHSUN U，MILLER D W.Dynamics and control of electromagnetic satellite formations［D］.Cambridge，MA:Massachusetts Institute of Technology，2007:1-58.

［7］SCHWEIGHART S A.Development and analysis of a high fidelity linearized J2model for satellite formation flying［D］.Cambridge，MA:Massachusetts Institute of Technology，2001.