水下通气空泡航行体结构模态及冲击响应研究
何乾坤,张嘉钟,魏英杰,王 聪
(哈尔滨工业大学 航天学院,150001 哈尔滨,heqiankun@foxmail.com)
水下航行体在水中运动时,其表面某些部位的压力会因绕流的作用而降低,从而产生空化现象[1].当流场发生空化后会产生强烈的噪声、冲击和振动,而且在不同空化数下包裹航行体的空泡形态不同,当航行体处于部分或全部空泡包裹状态下,由于空泡以及水的作用,航行体的振动特性也发生了改变,在此状态下,若依然采用真空中或完全沾湿状态下的动力学特性参数,就会对其动力学分析结果产生很大影响.因此,考虑通气空泡对于水下航行体的动力学特性影响显得更加重要.
近年来,很多学者都对空泡对水下航行体结构动力学行为的影响做了许多相关的研究.由于目前国内外还没有一套成熟的理论体系描述带空泡结构的振动,主要的方法都是基于有限元软件对其进行仿真,比如Adina、Ansys+CFX、Comsol、Abaqus+Fluent 等仿真软件.如E.Alyanak[2]研究了超空泡鱼雷的动力学行为,并对其结构进行了优化.M.Ruzzene[3]建立了超空泡水下航行体的尾部与空泡壁上下撞击的力学模型,并分析了在冲击力作用下航行体结构动力学响应.杨传武[4-5]采用有限元方法分析了超空泡水下航行体的固有特性,并计算了冲击载荷作用与动态轴向载荷作用下超空泡航行体的结构响应.尽管国内外对于超空泡水下航行体的振动有一定研究,然而对于通气空泡水下航行体的动力学特性研究依然较少,而航行体在被局部空泡包裹下力学环境更加复杂[6],结构破坏的风险更大[7].
本文分析了局部通气空泡包裹下的水下航行体动力学特性,将通气空泡简化为空气弹簧,考虑了通气空泡和水对于结构振动特性的影响,在此基础上建立了通气空泡水下航行体的简化理论模型及其流固耦合振动方程.基于该振动方程,利用有限元法求解了不同空化数下航行体的模态频率及振型,并将计算结果与通气空泡简化为真空的结果进行对比(为了清晰地表述两者之间的关系,将通气空泡简化为空气弹簧情况定义为状态1,而通气空泡简化为真空情况定义为状态2),分析了通气空泡对水下航行体的动力学特性影响.在此基础上,对结构施加一定的冲击载荷,得到结构响应随空泡长度的变化规律,并分析了通气空泡对响应的影响.
1 理论模型的建立
为了对通气空泡航行体建立合理的动力学方程,文中将其结构动力学模型分解为两个区域,如图1 所示.
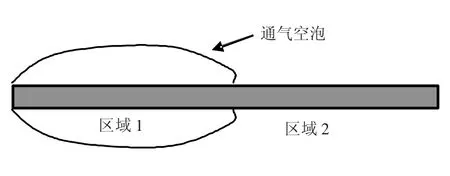
图1 计算模型
图中,区域1 被通气空泡包裹,通气空泡对其动力学方程中的刚度阵产生了影响,可以将通气空泡简化为空气弹簧建立其结构动力学方程;区域2 被水包裹,水主要对其动力学方程中的质量阵产生了影响,可以利用附加水质量理论建立其结构动力学方程.因此通气空泡运行航行体的结构动力学方程可以表示为
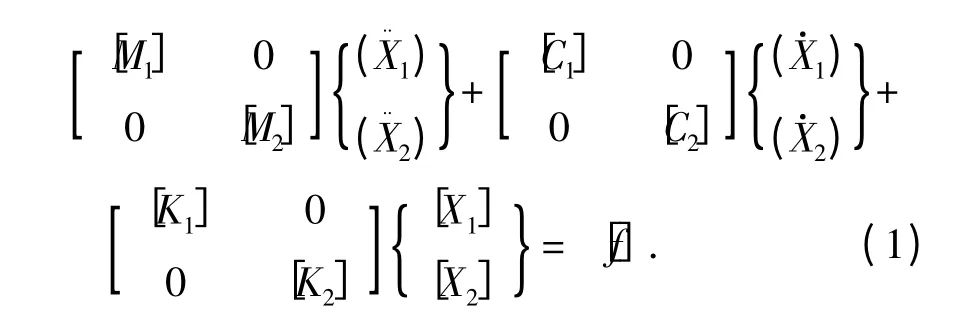
其中:[M1]、[M2]分别为区域1 和区域2 的质量阵,[M2]=[M]+[Ms],[M]为结构固有质量阵,[Ms]为附加水质量,由附加水质量理论可知ms=ρ(πR2),即等于单元长圆柱体排开的流体质量[8];[C]为结构阻尼阵;[K1]、[K2]分别为区域1 和区域2 的刚度阵,[K1]=[K]+[Ks],[Ks]为通气空泡产生的附加刚度;[X1]、[X2]分别为区域1 和区域2 的位移矩阵;[f]为载荷阵.
在状态1 分析中,将通气空泡简化为空气弹簧,[Ks]可以借助于空气弹簧理论推导得出.区域1 通气空泡对于结构的弹性作用取决于空泡内的气体压力p 和空泡的有效面积Ae,空泡上受到流体垂直载荷F 可表示为

假设航行体通气与泄气的气体质量均衡,即空泡内的压缩气体质量一定,当垂直空泡面流体载荷发生变化时,空泡直径会发生变化(即空泡的压缩或膨胀),同时空泡体积和空泡内压力也发生变化,在此可以假设其变化满足如下的气体状态方程(该假设只可用于通气空泡,因为自然空泡不满足该方程):

式中:p0、V0为稳定状态下空泡内压力和体积;p、V为扰动下空泡内压力和体积;m 为多变指数.
将式(3)代入式(2)得通气空泡受力
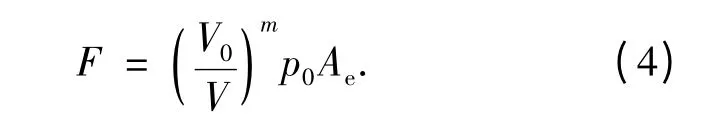
式中:空泡体积V、有效面积Ae均是空泡内压力p和空泡变形Δ 的函数(Δ=Rc-R,Rc为通气空泡半径,R 为航行体半径),即有V=V(p,Δ)和Ae=Ae(p,Δ).当空泡内外压差较大时,空泡内压力变化对于空化数影响非常微小,因此当空泡内压力在一定范围内变化时,忽略其对空泡体积和有效面积的影响,由此,空泡体积、有效面积可分别用V=V(Δ)和Ae=Ae(Δ)来表示.将式(4)对Δ 求导得出通气空泡的刚度特性为
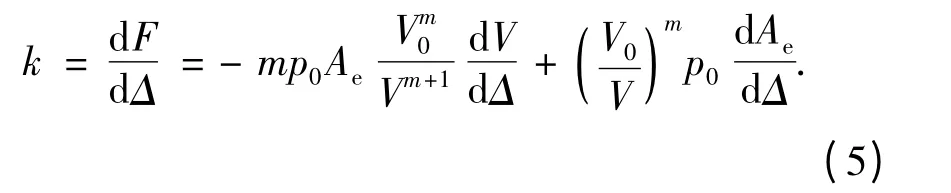
对于微振动过程中有(V0/V)≈1,并利用Ae=-dV/dΔ,可以得到稳定状态下,通气空泡刚度为
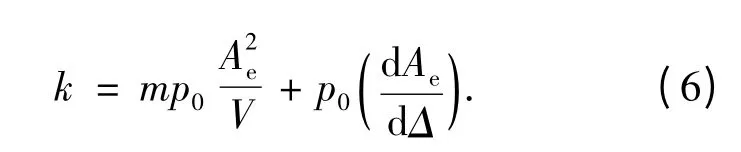
在空泡微振下,忽略空泡有效面积变化,即dAe/dΔ=0.式(6)表达为

式中k 与空泡内压力、以及空泡外形参数(有效面积和体积)有关;若假设航行体通气运行过程为等温过程,则可认为多变指数m=1[9-10].
若空泡的最大截面直径为Dc和空泡长度为Lc,且暂不考虑空泡尾部闭合点的脉动影响,则有效面积Ae=2πRLc.通气空泡体积V 为空泡轮廓所包含的体积减去航行体体积.其中,空泡轮廓所包含的体积为空泡界面S 沿空泡轴向[0,Lc]的积分[11](如图2).
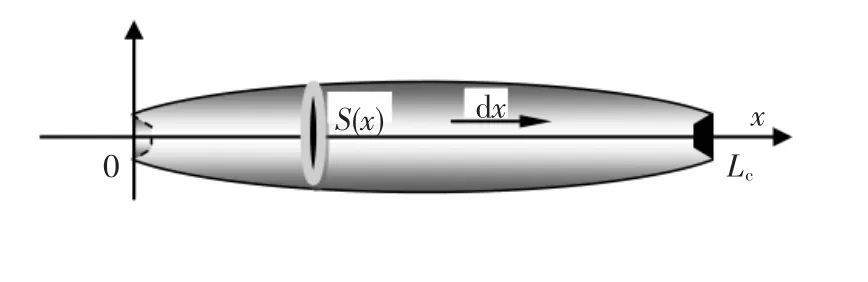
图2 空泡外形
空泡最大截面直径Dc和长度Lc可以根据Logvinovich 独立扩张原理[12-13]确定;其取决于空化器直径Dn,阻力系数Cx和空化数σ.在小空化数σ 下有
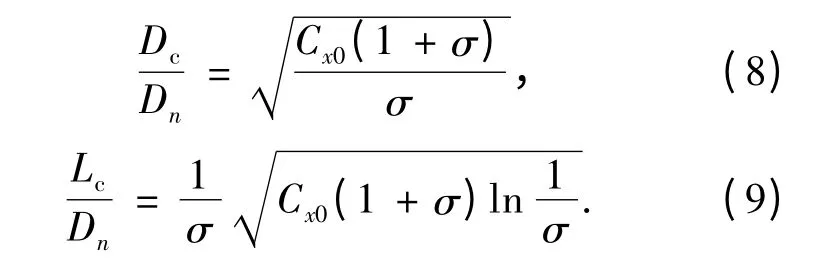
式中空化数σ 可以表达为
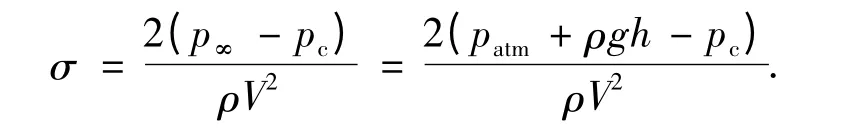
式中:p∞、patm分别为环境压力和标准大气压;h、V分别为运动深度和速度;pc表示空泡内压力.在小空化数下,钝空化器系数满足Cx=Cx0(1+σ),式中,Cx0为σ=0 时给定空化器的阻力系数值(对于自由流线流),90°圆盘空化器Cx0=0.82[14].
2 通气空泡航行体模态计算
通过以上的理论分析,给出了通气空泡航行体振动方程式(1),可以得出单元阵的表达方式,那么可利用有限元法对单元阵进行计算.分析长度L=8 m,截面直径D=0.5 m 的水下航行体.航行体密度ρ =2.7×103kg/m3,弹性模量为E=70 GPa,泊松比ν=0.3,通入气体压力p=0.3 MPa,航行深度h=20 m,以定常速度V 运动.对状态1 分析,通过式(8)、(9)可以得到不同速度V 下的空泡外形尺寸,代入式(7)可以得到简化空气弹簧的刚度.所得参数如表1 所示.
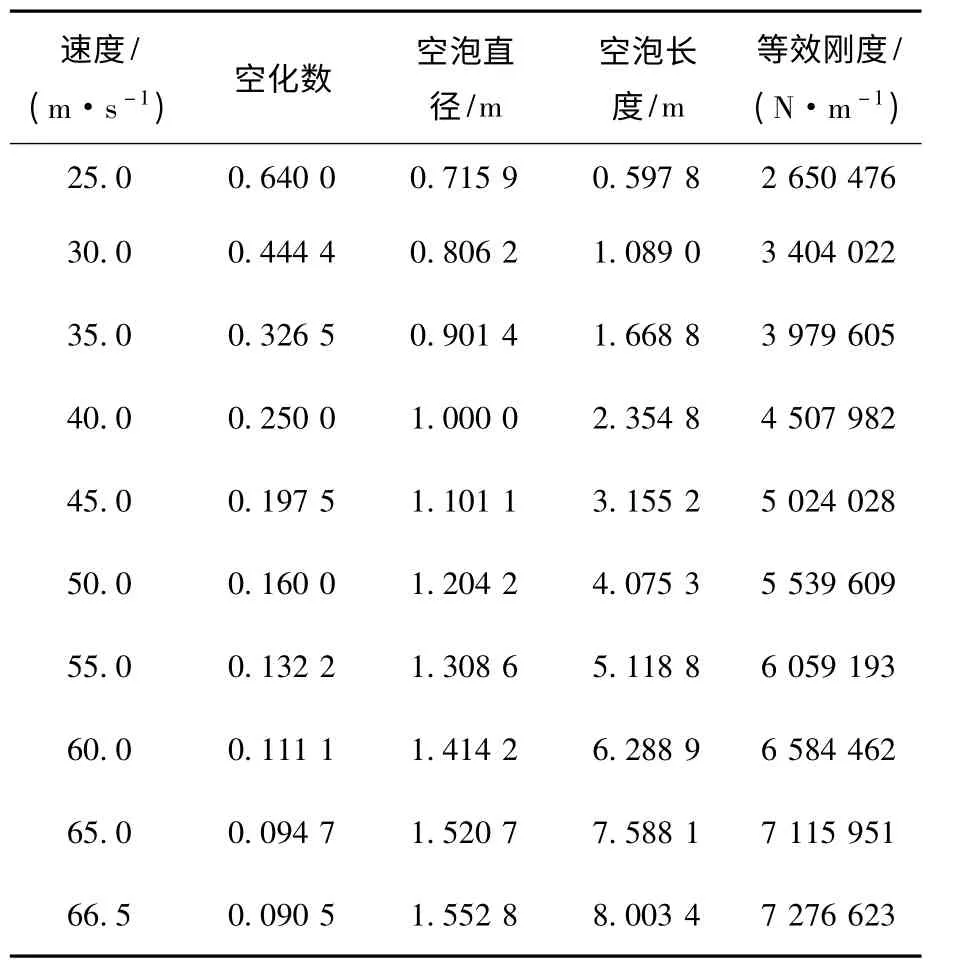
表1 不同速度下输入参数
通过表1 可以看出,随着速度的增大,通气空泡简化为空气弹簧的刚度也随之增大;将航行体简化为Euler-Bernoulli 梁模型,求解其在平面内的弯曲振动模态,梁两端均为自由,得到前三阶模态频率随空泡长度l(l=Lc/L 为无量纲空泡长度)的变化关系.图3 给出了状态1 通气空泡航行体模态频率随空泡长度的变化规律,可以看出随着空泡长度的增大,结构与水的接触面积减小,从而使水附加质量也随之减小,由于两者的共同作用,导致了结构模态频率随着空泡长度l 的增大而增大.图4 ~6 分别给出了航行体前3 阶模态振型随通气空泡长度的变化,图中横轴表示航行体的轴向坐标,竖向表示无量纲通气空泡长度l.
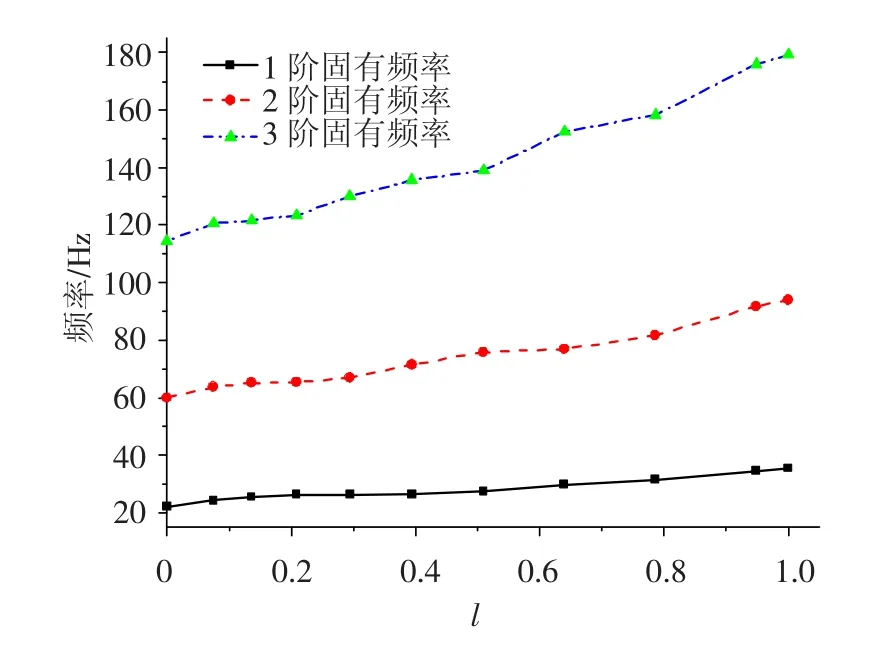
图3 状态1 模态频率随空泡长度变化
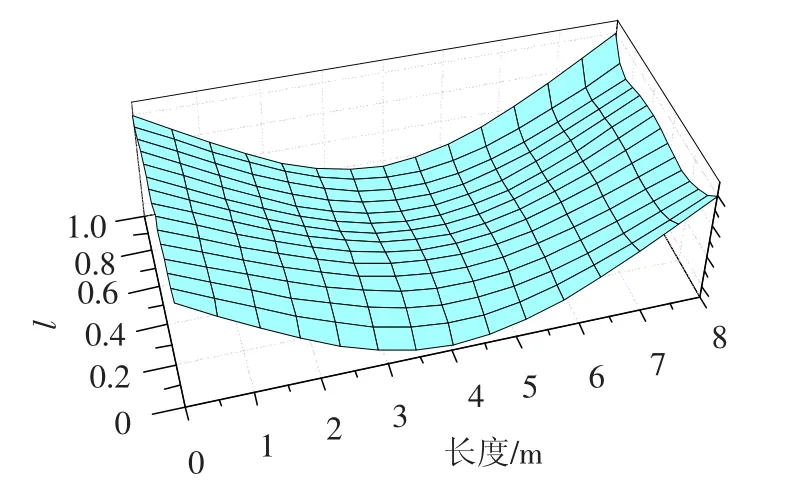
图4 第1 阶振型
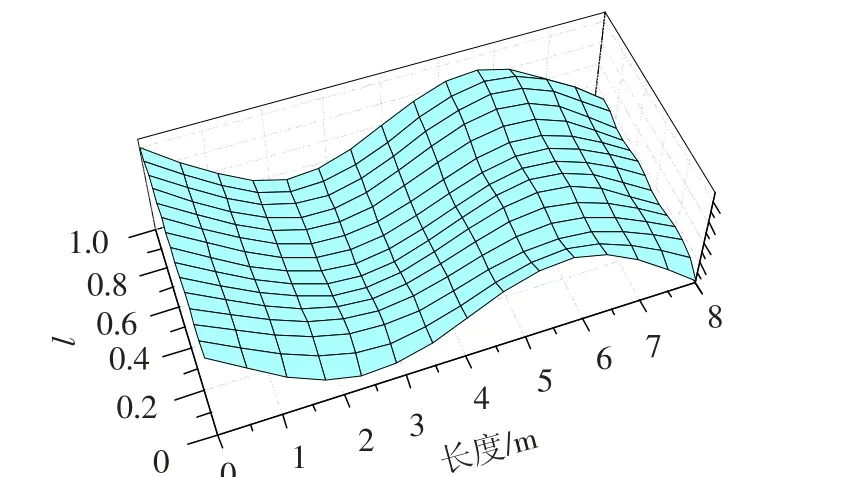
图5 第2 阶振型
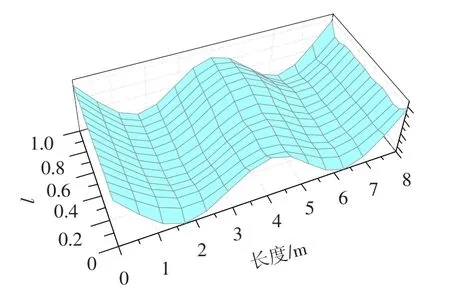
图6 第3 阶振型
为了更清晰地得到通气空泡对于结构的影响,本文对将通气空泡简化为真空的情况(即状态2,此状态中,[Ks]=0)结构模态频率进行了计算.从图7 ~9 中可以看出,状态1 的结构模态频率略大于状态2 的模态频率;通气空泡的附加刚度对于1 阶模态频率影响较大,并且随着模态阶数的增大,其影响逐渐减小.通过图7 ~9,还可以得到航行体模态频率随着空泡长度的增大是波动增大的,把波动规律与振型比较可以发现,各阶模态频率在振型腹点处都有较大的波动,而在振型的节点处,增大比较稳定.
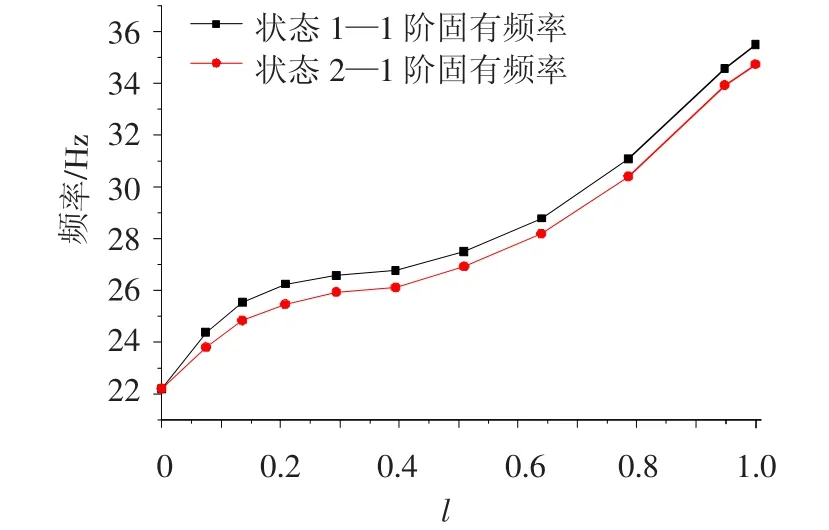
图7 状态1 与状态2 第1 阶模态频率比较
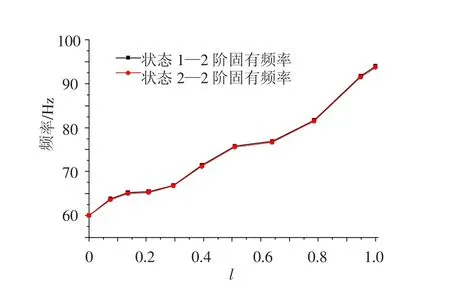
图8 状态1 与状态2 第2 阶模态频率比较
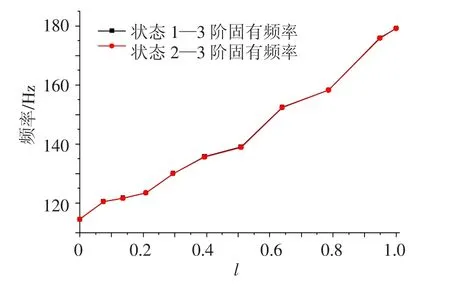
图9 状态1 与状态2 第3 阶模态频率比较
3 冲击载荷作用下通气空泡航行体响应
航行体在水下运行经常会受到横向流冲击,对于被不同通气空泡长度包裹下的航行体,当受到同样的冲击载荷作用时,所产生的响应有所不同.假设航行体整体受到1 个横向均布力冲击载荷,载荷变化如图10 所示,本文对通气空泡航行体受冲击后的响应进行计算.
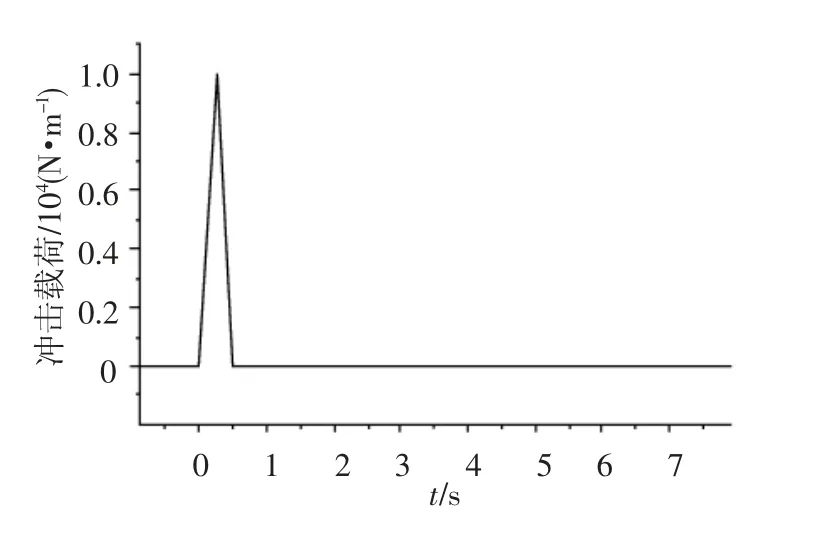
图10 冲击载荷
图11 给出了航行体中部一点的响应,两种状态下,由于附加水质量和水作用面积的减小,结构位移响应的周期和幅值均随着空泡长度的增大而减小;在相同空泡长度下,状态1 的幅值和周期小于状态2 的结果,可以得出通气空泡的刚度对结构振动的周期和幅值有一定的影响,减小了结构响应的周期和幅值.
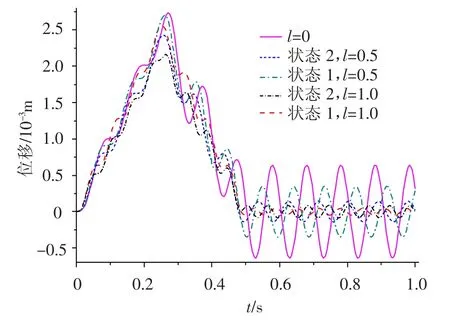
图11 位移响应
4 结 论
本文通过对通气空泡航行体的结构进行简化,将航行体分解为两个区域,区域1 将通气空泡简化为空气弹簧,区域2 将水简化为附加质量,得出在通气空泡与水两者共同作用下的结构动力学方程.利用有限元法对动力学方程进行离散求解,得出结构的模态随空泡长度的变化规律,并且分析了通气空泡对于结构动力学特性的影响.通过分析得出以下结论:
1)随着通气空泡长度的增大,结构的模态频率呈波动增大趋势;
2)通气空泡弹性对于1 阶模态频率影响较大,而且随着模态阶数的增大,其影响越来越小;
3)受横向冲击振动后,航行体位移响应的周期和幅值均随着空泡长度的增大而减小;
4)在相同空泡长度下,采用空气弹簧理论简化通气空泡的航行体受冲击振动后,响应幅值和周期小于将通气空泡简化为真空的结果.
[1]魏海鹏,郭凤美,权晓波.潜射导弹表面空化特性研究[J].宇航学报,2007,28(6):1507-1523.
[2]ALYANAK E,VENKAYYA V,GRANDHI R,et al.Structural response and optimization of a supercavitating torpedo[J].Finite Elements in Analysis and Design,2005,41(6),563-582.
[3]RUZZENE M,SORANNA F.Impact dynamics of elastic stiffened supercavitating underwater vehicles[J].Journal of Vibration and Control,2003,23(10):243-267.
[4]杨传武,王安稳.冲击载荷作用下超空泡水下航行体的结构响应[J].华中科技大学学报(自然科学版),2008,36(7):129-132.
[5]杨传武,王安稳.动态轴向载荷对超空泡航行体振动特性的影响[J].华中科技大学学报(自然科学版),2008,36(12):71-74.
[6]KOROVKIN A N,LEVKOVSKII YU L.Study of the collapse of a cavitation cavity close to a solid wall[J].Journal of Engineering Physics and Thermophysics,1967,12:127-131.
[7]BENJAMMIN T B,ELLIS A T.The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries[J].Philosophical Transaction of the Royal Soicety of Lond,1996,260(1110):221-240.
[8]王献孚,熊鳌魁.高等流体力学[M].武汉:华中科技大学出版社,2003.
[9]郑明君,陈潇凯,林逸.空气弹簧力学模型与特性影响因素分析[J].农业机械学报,2008,39(5):10-14.
[10]郑明君,王海花,王渊.空气弹簧弹性特性理论分析与试验研究[J].噪声与振动控制,2009(3):43-46.
[11]VASIN A D.The principle of independence of the cavity sections expansion(logvinovich’s principle)as the basis for investigation on cavitation flows[C]//RTO AVT Lecture Series on“Supercavitating Flows”2001.Belgium:RTO EN-010,2001,8:1-27.
[12]SEMENENKO V N.Computer simulation of unsteady supercavitating flows[C]//AGARD FDP Workshop on“High Speed Body Motion in Water”.Kiev,Ukraine:[s.n.],1997,22:1-10.
[13]LOGVINOVICH G V.Hydrodynamics of flows with free boundaries[M].Kiev,Russian:Naukova Dumka Publing House,1980.
[14]MAY A.Water entry and the cavity-running behavior of missiles[R].Maryland:NTIS,1975.

