星载SAR LFM信号在轨相位预失真补偿方法
孙吉利,张 平,杨汝良
(中国科学院电子学研究所,100190 北京,sun9721@sohu.com)
星载SAR LFM信号在轨相位预失真补偿方法
孙吉利,张 平,杨汝良
(中国科学院电子学研究所,100190 北京,sun9721@sohu.com)
由于空间环境下星载合成孔径雷达(SAR)系统相位误差会发生漂移,影响线性调频(LFM)信号的脉冲压缩性能,因此本文提出一种基于多项式拟合的在轨相位预失真补偿方法.通过在轨定标可获得系统相位误差,在地面对其进行多项式拟合得到相位补偿参数,上注相位补偿参数,在轨运算生成具有补偿相位的线性调频信号.给出了该方法的理论依据和实现流程,分析了星上硬件资源需求和优缺点.通过相位预失真补偿仿真和真实系统试验,并与其它方法结果进行比较,证明该方法可以有效地改善线性调频信号的脉冲压缩性能.
星载SAR;线性调频信号;多项式拟合;相位预失真
星载合成孔径雷达(SAR)系统采用宽带线性调频(LFM)信号来获得高分辨率.伴随着目标识别要求的提高,对分辨率的要求也越来越高,导致信号频带变得越来越宽.星载SAR高分辨率成像通常要求系统带内相频波动小于5°,在实际SAR中往往通过相位校准和相位预失真补偿相结合的办法来实现.
国内外学者对LFM信号的产生和预失真做了大量研究,文献[1-2]提出两种宽带LFM信号产生技术,并分别分析了信号产生质量;文献[3-4]对线性调频波形产生器的相位误差进行了影响分析,深入探讨了周期相位误差、一次相位误差、二次相位误差、高次相位误差和随机相位误差对输出信号脉压性能的影响;文献[5]对相位误差提取和时域预失真补偿进行了描述,并在ISAR试验雷达上进行了试验验证.
尽管对LFM信号的研究非常深入,但均未涉及星载SAR的在轨相位预失真补偿问题.目前国内外的星载SAR系统,普遍采用数字波形存储技术(DDWS)来产生宽带LFM信号,并通过发射前的地面定标校准,实现一次性相位预失真补偿.星载SAR在轨运行阶段,当空间环境变化导致系统相位特性发生偏移后,地面预失真补偿与系统相位误差失配,导致LFM信号脉压性能变差.现有相位补偿方法需要将所有LFM信号波形数据上传,但这会长时间占用卫星测控通道,因此目前尚无实际应用.
本文针对目前星载SAR系统在轨相位预失真补偿存在的问题,创新性地提出了多项式拟合相位预失真(Polynomial Fitting Phase Pre-distortion,PFPP)补偿方法.采用该方法,并利用直接数字频率合成 (Direct Digital Frequency Synthesis,DDFS)技术,可在轨生成具有补偿相位的中频LFM信号.文中给出了PFPP方法的理论依据,以及在轨相位预失真补偿的实现流程,提出采用多项式分解形式以适应流水线计算并提高运算精度,分析了该方法占用的硬件资源以及与直接数字波形合成(Direct Digital Wave Synthesis,DDWS)方法相比的优缺点.基于真实星载SAR系统,采用DDFS+PFPP的方法进行了相位预失真补偿试验,并与DDWS方法相位预失真补偿结果进行了比较,试验结果验证了其有效性.
1 星载SAR系统相位失真
LFM信号的脉冲压缩通常通过匹配滤波实现,其压缩结果高度依赖于收发LFM信号的相位一致性.然而星载SAR系统中存在相位失真,影响LFM信号的脉压性能.

图1 星载SAR系统简化
D/A产生的LFM信号经过滤波、混频、放大后通过天线发射出去,地物反射信号经天线接收后放大、混频、滤波,最终由A/D采集.该过程中发射、接收通道均对调频信号产生相位的畸变,影响LFM信号脉冲压缩后的主瓣宽度、峰值旁瓣比(PSLR)和积分旁瓣比(ISLR).
该过程造成的相位失真误差,可分为确定性误差和随机误差.随机误差指相位误差的变化规律是随机的,主要使系统冲击响应的积分旁瓣比下降,引起图像对比度下降.确定性误差指相位误差的变化规律是确知函数,包括线性相位误差(一次相位误差)、二次相位误差和高次相位误差[3-4].
线性相位误差(一次相位误差)只影响冲激响应的位置,而对其形状无任何影响.二次相位误差相当于改变了回波多普勒信号的调频斜率,使匹配滤波器失配,因而导致主瓣宽度展宽,主瓣峰值下降,旁瓣电平增高,引起图像分辨率损失,图像对比度下降.高次相位误差使系统冲激响应产生不对称的旁瓣,在造成主瓣轻微畸变的同时使一侧旁瓣电平增高,引起图像对比度下降.
2 时域相位预失真补偿
通过地面或者在轨的定标,可以获得发射、接收通道造成的相位失真误差,通过预先对D/A输出的LFM信号进行反向的相位补偿,可以抵消发射、接收通道造成的确定性相位误差,该过程称作LFM信号的相位预失真补偿.
星载SAR发射的信号形式为
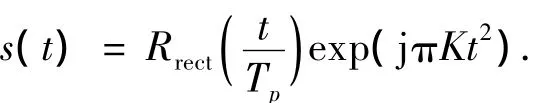
其频谱表达式为[6]
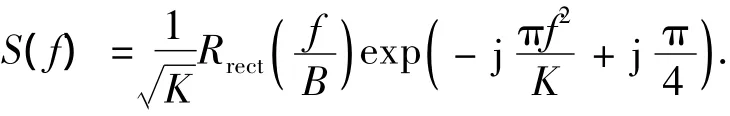
假设发射、接收通道造成的相位畸变可用如下传递函数来表示:

那么,理想LFM信号经上述畸变后输出信号的频谱为
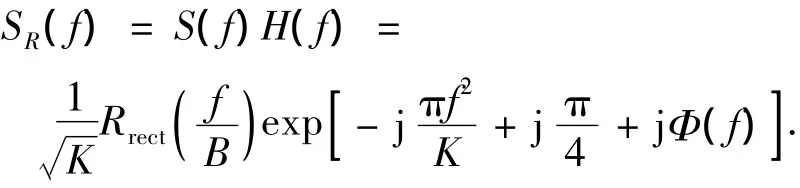
输出信号在时域可表示为

假设系统的幅频特性和相频特性都是频率的缓变函数,系统的延迟时间可以忽略,应用驻定相位原理并忽略Φ(f)二次以上的高次项,积分的结果可近似为
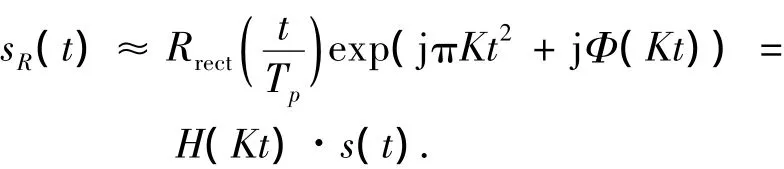
上式说明LFM信号通过一延迟时间可忽略不计的线性系统时,其输出信号相当于系统频域特性与LFM信号的乘积.根据驻定相位原理,当时带宽积较大时,LFM信号在每个频率取f=Kt处都驻留了相当长的时间,线性系统在此时间内己达到稳定状态,时域信号就为线性系统传递函数H(Kt)与输入LFM信号之积[3].
以上的分析说明,在时域将发射LFM信号s(t)乘以H(Kt)的倒数即可实现相位预失真补偿,即将发射信号变为
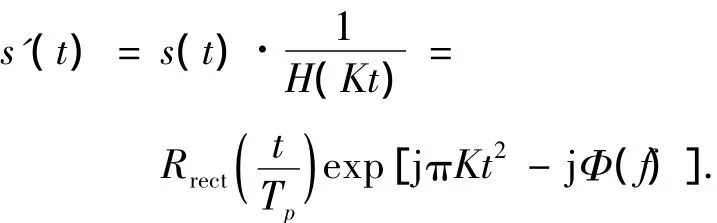
经相位畸变后输出信号时域表示为
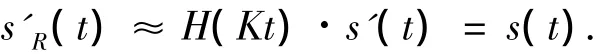
在实际应用中,通过点目标信号或者定标信号来获得系统相位失真,在发射LFM信号中加入预失真补偿相位,从而使接收采集的LFM信号相位接近理想相位.
3 中频LFM信号在轨相位预失真补偿
3.1 实现方法
高分辨率星载SAR要求宽带LFM信号具有极高的调频线性度以及频率稳定度,模拟方法(例如采用SAW器件的无源法,采用VCO器件的有源法)均无法满足.随着数字电路技术的发展,数字方法产生宽带LFM信号成为可能,目前常用的直接数字合成(DDS)技术有两种:直接数字波形合成(Direct Digital Wave Synthesis,DDWS)和直接数字频率合成(Direct Digital Frequency Synthesis,DDFS)[7].
DDWS也就是数字波形存储的方法,在地面将生成的数字波形数据写入固态存储器中,通过读取波形数据,由高速D/A产生相应的LFM信号.目前国内外的星载SAR系统中,宽带LFM信号的产生普遍采用DDWS技术,并且相位预失真方法成熟[8-10].
DDFS技术是从相位的概念出发进行频率合成,具有精确相位、频率分辨率高等优点.利用DDFS技术,本文提出的LFM信号的多项式拟合相位预失真PFPP方法实现如图2所示.
该方法在轨计算中频LFM信号的累加相位和预失真补偿相位,将分别计算的两个相位进行累加,得到进行预失真补偿后的LFM信号相位,查表获得输出信号波形数据.LFM信号的中频直接产生相对于基带产生具有信号正交性好、模拟环节简单、设计灵活等优点.生成的中频LFM波形数据存储于SRAM中,LFM信号输出时D/A直接读取SRAM中的数据.
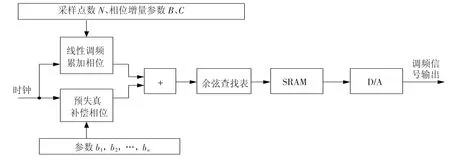
图2 中频LFM信号在轨相位预失真补偿实现
该方法仅需要地面上发参数:采样点数N、相位增量参数B、C和预失真补偿系数b1,b2,…,bn,就能够实时产生含有补偿相位的中频LFM信号,避免了大量数据上传占用卫星测控通道.按照采样点数N、相位增量参数B、C计算LFM累加相位,根据预失真补偿系数b1,b2,…,bn计算预失真补偿相位,从而获得LFM累加相位φA(i)和预失真补偿相位φE(i),最终生成具有补偿相位的中频LFM信号为
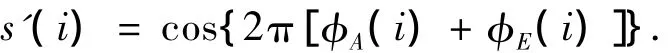
3.2 相位预失真补偿步骤
在轨进行相位预失真补偿的实现步骤如下:
1)地面首先上注需要补偿的中频LFM信号参数采样点数N、相位增量参数B、C,将预失真补偿系数 b1,b2,…,bn设为0,产生无相位预失真的中频LFM信号;
2)进行在轨定标,获得含系统相位失真的定标数据,将定标原始数据下传至地面;
3)在地面通过定标数据提取失真相位,通过多项式拟和得到相位预失真补偿系数;
4)通过地面指令上发预失真补偿系数b1,b2,…,bn,重新生成中频LFM波形数据,实现中频LFM信号的在轨预失真补偿.
3.3 中频LFM信号的相位计算
中频LFM信号在时域可表示为
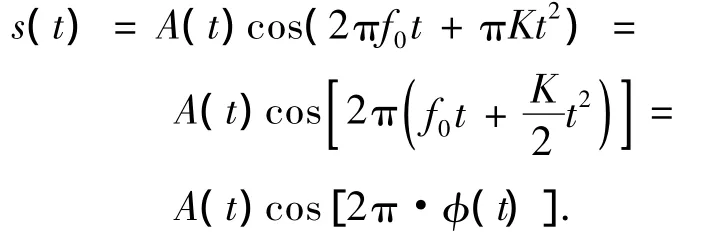
其中:-T/2≤t≤T/2,T是调频信号时域宽度;K是调频斜率;f0是调频信号的中频;A(t)是实包络,LFM信号产生时可以定义为常量.时域相位2πφ(t)决定了信号的LFM特性,其中φ(t)=f0t+Kt2/2.
进行离散化处理,令t=i/fs,则相邻采样点间的φ(t)增量可表示为

从而获得可累加计算的LFM相位为
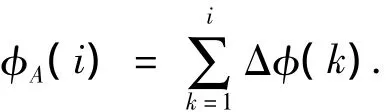
由于D/A输出的采样率fs固定,因此式(1)中B项和C项仅由发射中频f0和调频斜率K决定.相位计算过程中各参数的量化造成的相位误差主要是一次相位误差,仅影响脉压后的主瓣位置.
3.4 相位预失真补偿系数提取
发射、接收通道造成的相位误差归一化后可用n次多项式表示,按照D/A输出的采样率fs进行离散化后可表示为

式中:0<i≤T·fs;ΦR为采集到的基带LFM信号的时域相位;Φ0为理想基带LFM信号的时域相位.在这里将Φ0和ΦR的采样率通过插值处理统一至DA输出的采样率fs,多项式系数ak,k=0,1,2,…,n可通过定标数据拟合获得.
多项式中的常数项a0(即常数相位差)不影响成像质量,可以忽略.在实际运算过程中,由于in非常大,会导致an相对于a1非常小,采用硬件定点运算会产生较大的量化误差.因此需要变换上式为以下形式:
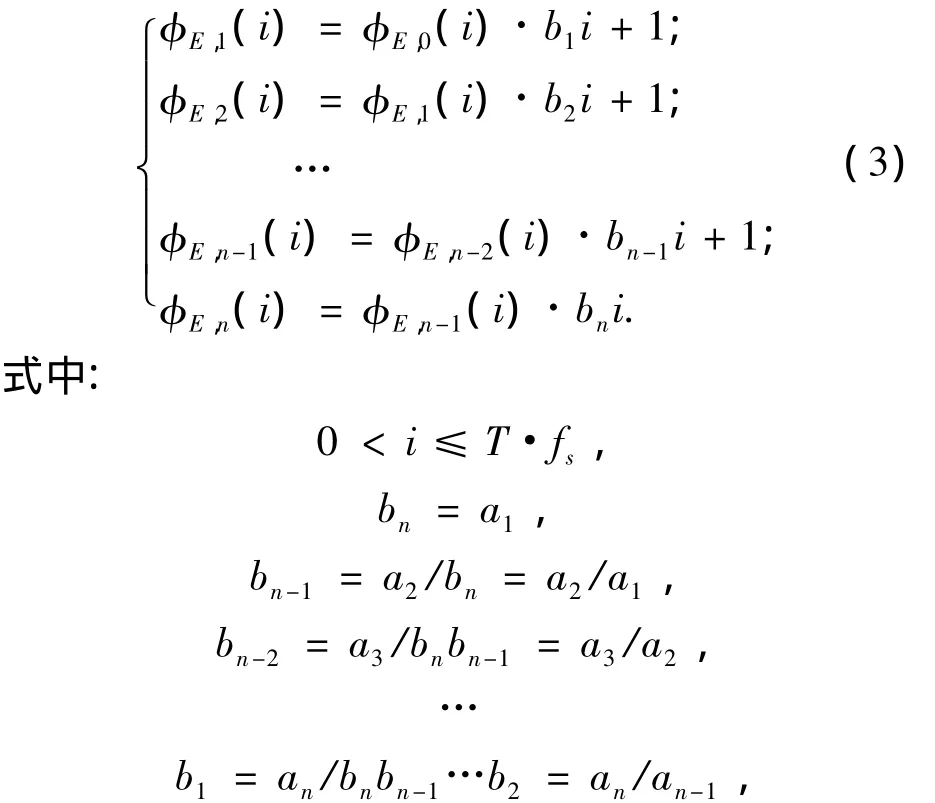
令 φE,0(i)=1,则除常数项外 φE,n(i)等效于φE(i).
通过变换,可使运算系数b1,b2,…,bn处于基本相同的数量级上,从而降低硬件实现的乘法器、加法器位数,使得更加有利于流水运算.
3.5 与DDWS方法的比较
以某星载SAR系统为例,该星载SAR系统采用中频 LFM直接产生技术,发射中频为300 MHz.高速D/A的采样率为1 200 MHz,量化位数为8 B.该星载SAR系统设计采用8种时宽、带宽组合的中频LFM信号,其参数如表1所示.

表1 某星载SAR的LFM信号模式
以下分别从存储资源占用量、相位预失真补偿难度以及LFM信号波形数据精度3方面对DDWS方法和本文方法进行比较.
1)存储资源占用量.如果采用直接数字波形合成DDWS方法,即将所有波形数据预先存储于固态存储器中,则需要的存储量为
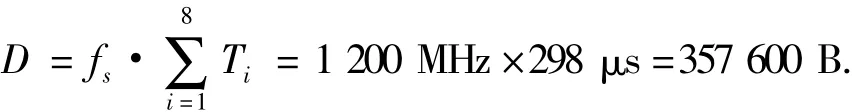
而本文提出的在轨计算方法所需的存储量不仅包括波形数据存储,还包括余弦查找表占用的存储资源,假设余弦查找表输入采用14位地址,则总存储量为

仅为DDWS方法的21.4%,而且随着星载SAR系统LFM信号模式的增多,这个比例会大大减小.
2)在轨相位预失真补偿的实现.DDWS相位预失真补偿方法即波形数据更新写入方法,在轨相位补偿需要将所有LFM信号波形数据上传,长时间占用卫星测控通道,这对于资源紧张的星地传输链路来说是不可取的.
而DDFS+PFPP方法仅需要上传n+3个参数,即可实现任意时宽带宽组合LFM信号的生成以及相位补偿.DDFS+PFPP方法通过在轨计算产生波形,每产生1个数据需要进行n+1次乘法和n+3次加法运算,为了保证运算精度,应采用32位乘法和加法运算.LFM信号的相位计算和查表过程可采用CPU或者FPGA实现,运算可在星载SAR工作间歇时完成,因此并不额外占用硬件资源.
3)LFM信号波形数据精度.DDWS相位预失真补偿方法即波形数据更新写入方法,其波形数据通过Matlab等浮点计算软件进行逐点插值时域相位补偿,不需要多项式拟合,运算精度较高,其波形数据中存在的主要误差为定点数据产生时的量化误差.
采用DDFS+PFPP方法产生LFM信号波形数据的误差包括上传参数的量化误差、数据运算过程中的截断误差以及查表操作引入的量化误差.上传参数的量化误差会造成LFM信号中频和调频斜率的偏离,可以通过适当选择LFM信号参数来减小或消除;数据运算过程中的截断误差以及查表操作引入的量化误差会使LFM信号输出信噪比降低,数据运算过程中的截断误差可以通过提高乘法器和加法器的位数来改善,查表操作引入的量化误差可以通过增加余弦查找表的容量来改善.
4 仿真和试验验证
以表1中时宽为46 μs,带宽为120 MHz的LFM信号为例,利用星载SAR模样系统进行仿真和地面模拟试验,对PFPP+DDFS的在轨相位预失真方法进行验证.中频LFM信号在轨波形数据计算和相位预失真均在FPGA中实现,其中上注参数、运算过程均采用32位量化,余弦查找表容量为16 kB,高速D/A的采样率为1 200 MHz,量化位数为8 B,LFM信号中频为300 MHz.
4.1 原始中频LFM信号波形数据产生
首先输入3个参数:采样点数N=55 200、相位增量参数 B=0.25、C=0.905 797 1×10-6,将预失真补偿系数 b1,b2,…,bn设为 0.采用Modelsim对FPGA运算进行仿真,产生的中频LFM信号幅频如图3所示.可以看出生成的中频LFM信号波形数据具有较高的信噪比,带内平坦度良好,带外杂散低.
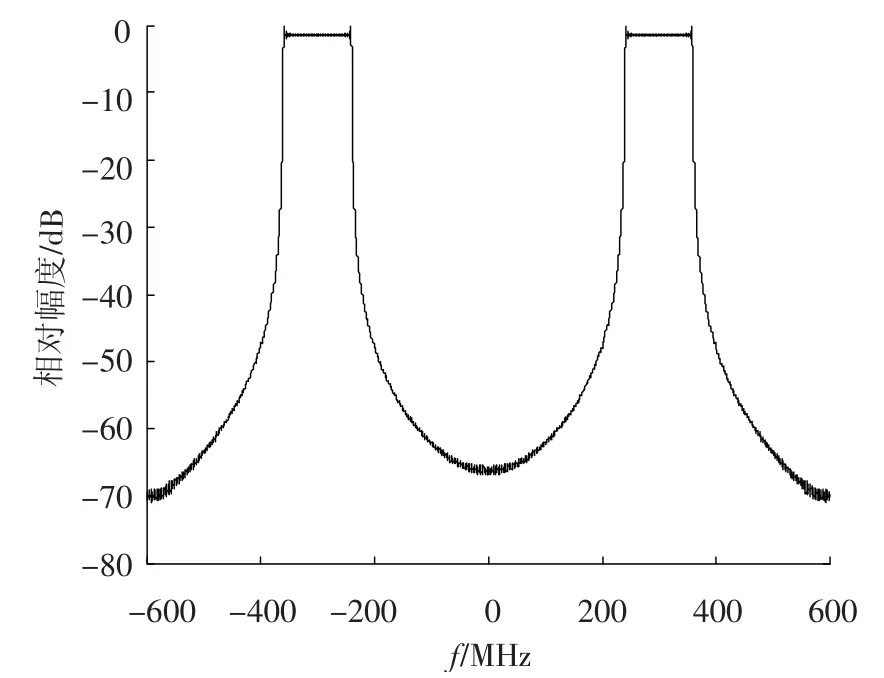
图3 中频LFM信号(仿真数据)幅频
4.2 定标信号采集
该中频LFM信号波形数据经过D/A转换、滤波、发射通道、定标回路、接收通道之后,由A/D直接采集中频信号,经过数字解调、低通滤波后得到的基带定标信号时域波形和幅频如图4所示.
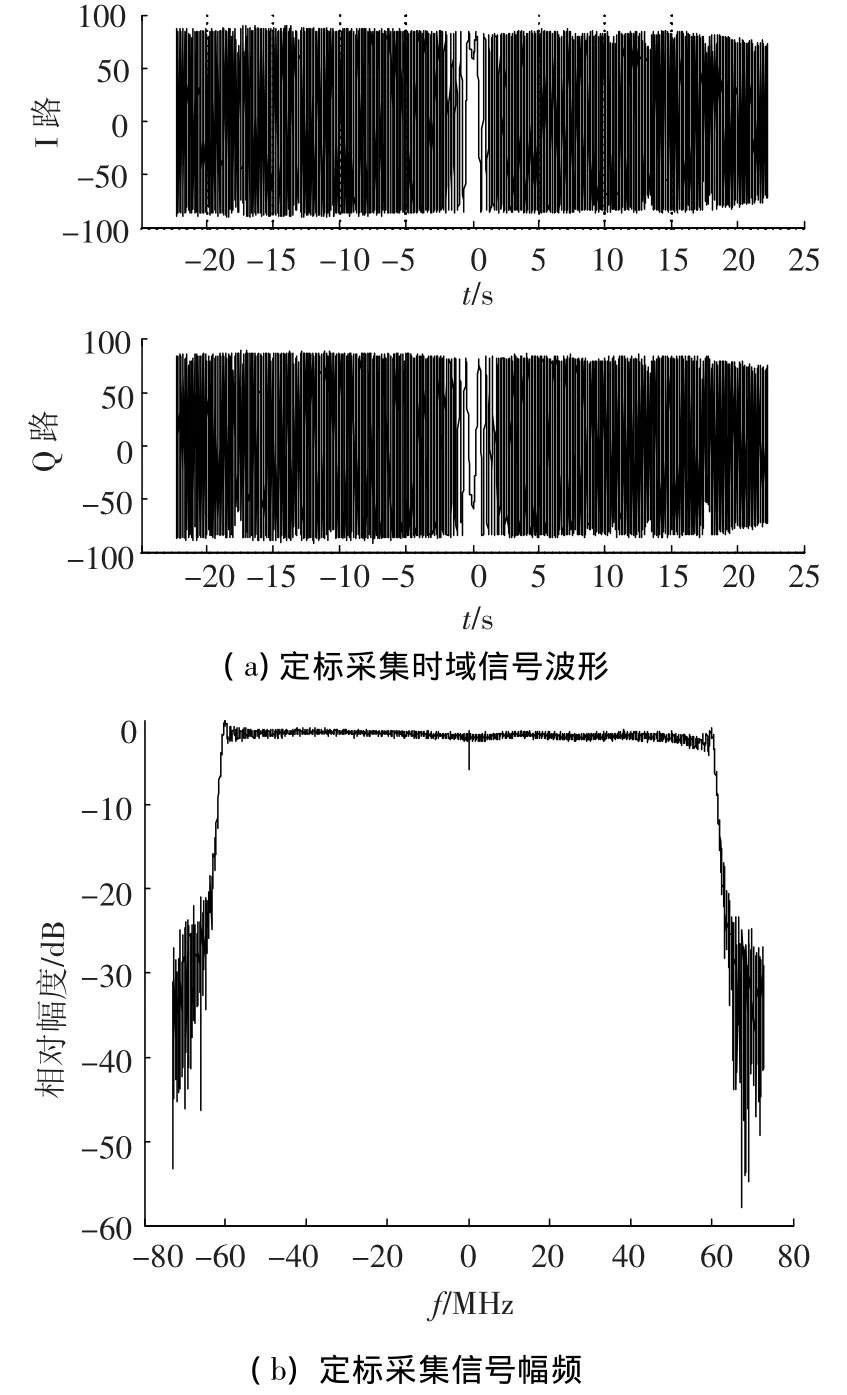
图4 定标采集信号时域波形和幅频
在Matlab中采用理想匹配滤波器对基带信号进行脉压处理,得到结果如图5所示.
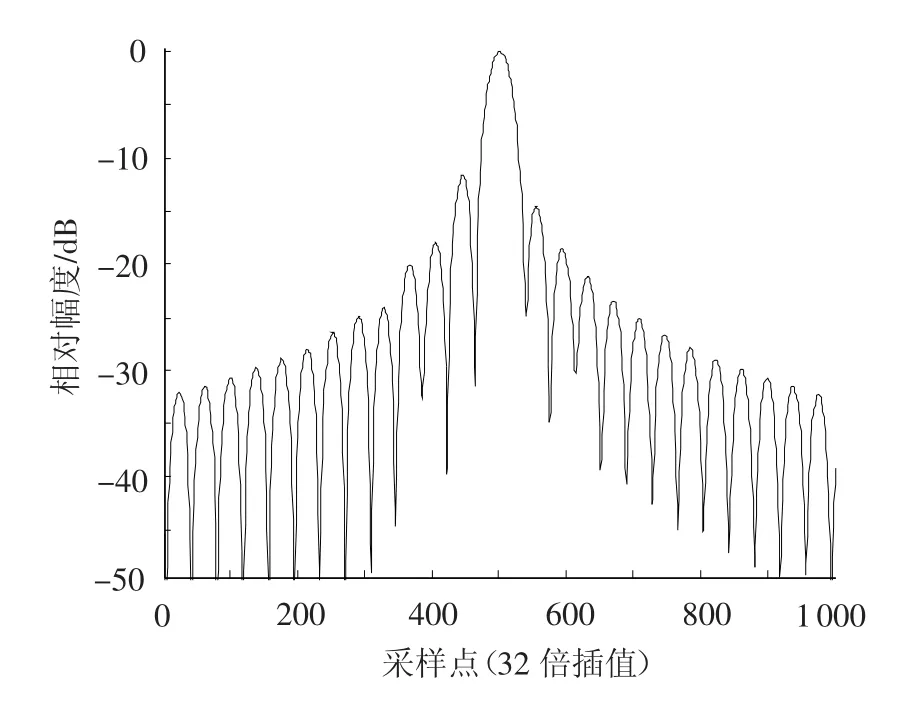
图5 相位预失真补偿前定标采集信号脉压结果(未加权)
可以看出峰值旁瓣比较高,并且旁瓣不对称,说明由该星载SAR系统收发通道造成的相位误差主要是高次相位误差.脉压结果的主瓣展宽和积分旁瓣比都比较正常,说明相位失真中二次相位误差较小,即在轨实时计算产生的中频LFM信号的调频率误差小.
4.3 相位预失真补偿系数提取
由于随机相位误差零均值正态分布,通过提取32帧定标数据进行平均,减小随机相位误差的影响,从而获得确定性相位误差.
采用10次多项式进行拟合,得到式(2)所示多项式,其中ai的值如下所示:
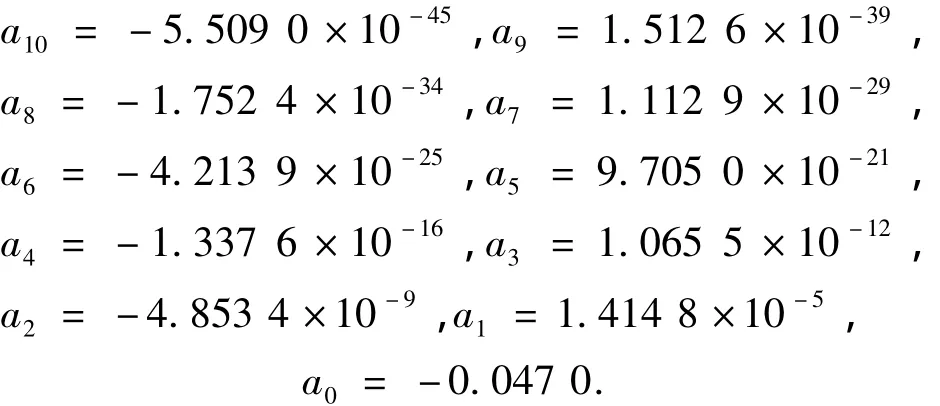
为提高运算效率和精度,将相位误差多项式转换为式(3)所示的流水计算形式,其中bi的值为
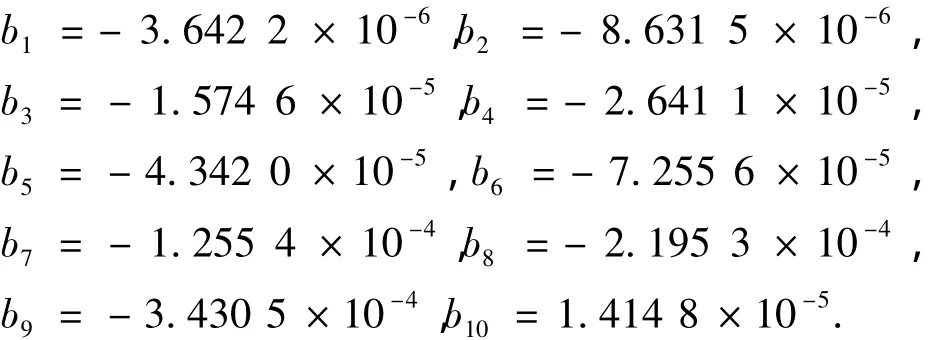
4.4 相位预失真补偿结果
将计算得到的预失真补偿系数 b1,b2,…,bn输入到FPGA中,保持采样点数N、相位增量参数B、C三个参数不变,重新进行定标数据采集.
预失真补偿前相位误差以及多项式拟合补偿后的相位误差如图6所示.
采用理想匹配滤波器进行脉压处理,得到脉压结果如图7所示.
可以看出,通过相位预失真补偿后,旁瓣变得对称,峰值旁瓣比、积分旁瓣比均有所改善,主瓣展宽未有明显变化.
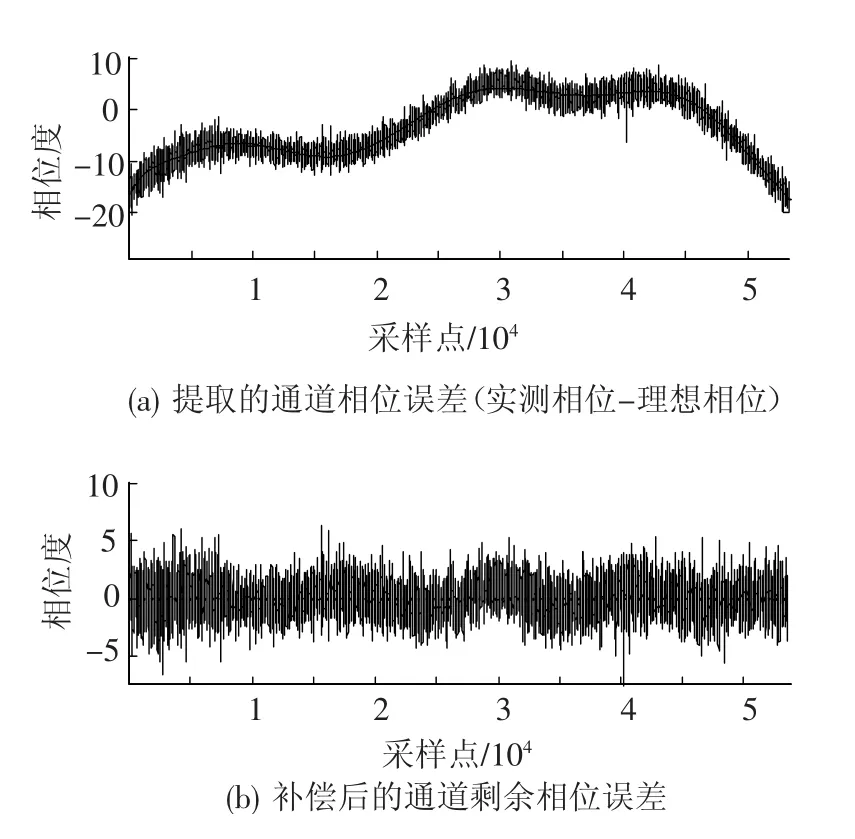
图6 提取的相位误差和补偿后的剩余相位
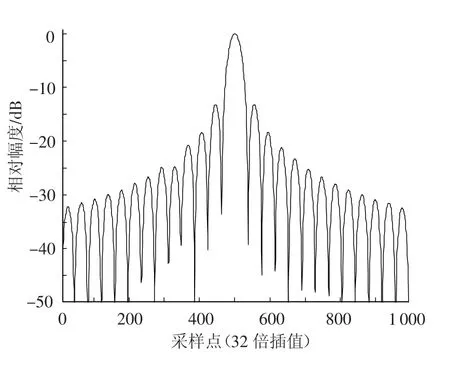
图7 相位预失真后定标采集信号脉压结果(未加权)
4.5 试验结果对比
将LFM信号分别采用文献[9]中的DDWS方法和DDFS+PFPP方法在星载SAR模样系统中进行相位预失真补偿试验,中频接收机采集得到的原始数据 (T=46 μs,B=120 MHz,f0=300 MHz)在Matlab软件中进行脉压处理,得到的未加权和Hamming窗加权脉压结果如表2所示.
从表2可以看出两种补偿方法得到的结果相近,均能够满足系统指标要求,但DDWS方法仅适应于地面应用,而将DDFS+PFPP方法应用于星载SAR可以实现在轨的相位预失真补偿.
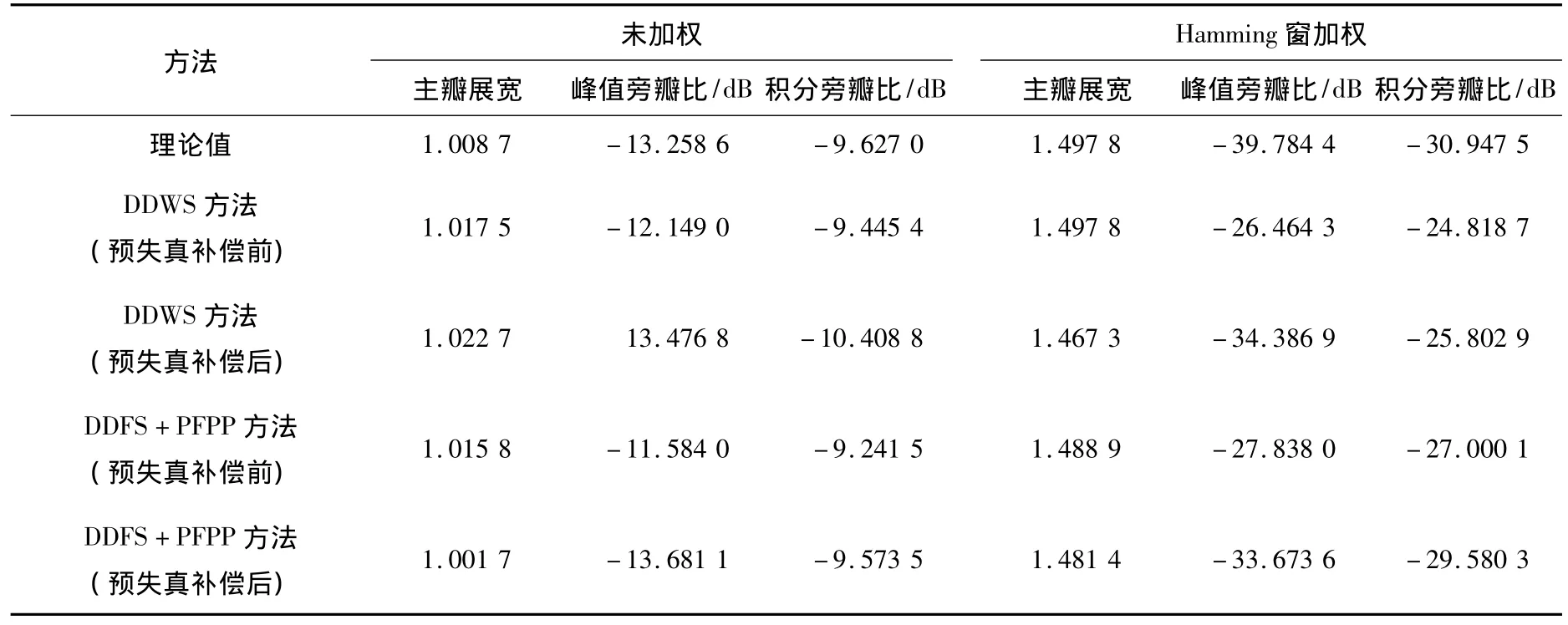
表2 两种相位预失真补偿方法脉压结果对比
5 结语
本文提出一种基于多项式拟合的LFM信号相位预失真补偿方法PFPP,该方法结合直接数字频率合成DDFS技术,可实现星载SAR的在轨相位预失真补偿,该方法已经在某星载SAR模样系统上成功应用.
本文中采用的LFM信号中频直接产生方法,相对于基带产生方法生成的信号正交性高,但信号带宽较小.为提高信号带宽,可以将DDFS+PFPP方法应用于LFM信号的基带产生,对基带I、Q通道分别进行补偿,以生成更大带宽的低相位畸变LFM信号.
随着星载SAR分辨率要求的提高,对星载SAR系统相频特性的无畸变要求越来越高,本文方法在不增加卫星测控通道负担的前提下,实现了LFM信号的在轨相位预失真补偿,相比传统方法更加具有工程应用价值.
[1]GRIFFITHS H D,BRADFORD W J.Digital generation of high time-bandwidth product linear FM waveforms for radar altimeters[J].IEEE Proceedings-F,1992,139(2):160-169.
[2]ZHU Mingbo.A high performance UWB LFM waveform generator[J].Journal of Electronics(China),2008,25(6):774-779.
[3]胡仕兵,汪学刚,姒强.线性调频波形产生器相位误差影响分析[J].电子测量与仪器学报,2008,22(2):101-106.
[4]POSTEMAN G B.Generation and performance analysis of wideband radar waveforms[C]//IEEE International Radar Conference.Piscataway:IEEE,1987:310 -314.
[5]杨文军,徐泳,王峰,等.宽带雷达系统失真补偿信号的提取方法[J].现代雷达,2006,28(5):8-11.
[6]赵树杰.雷达信号处理技术[M].北京:清华大学出版社,2010:139-162.
[7]霍志勇,张军.DDS线性调频信号产生技术研究[J].无线电工程,2006,36(1):27 -29.
[8]万永伦,姒强,吕幼新,等.DDWS的波形误差校正算法及实现[J].系统工程与电子技术,2006,28(2):209-211.
[9]NETTERSTROM A.Using digital pre-distortion to compensate for analog signal processing errors[C]//IEEE InternationalRadarConference.Piscataway:IEEE,1990:243-248.
[10]WANG Peng,MENG Huadong,WANG Xiqin.Suppressing autocorrelation sidelobes of LFM pulse trains with genetic algorithm[J].Tsinghua Science and Technology,2008,13(6):800 -806.
In-orbit phase pre-distortion of LFM signal for spaceborne SAR
SUN Ji-li,ZHANG Ping,YANG Ru-liang
(Institute of Electronics,Chinese Academy of Sciences,100190 Beijing,China,sun9721@sohu.com)
In spaceborne SAR(Synthetic Aperture Radar),the pulse compression of LFM(Linear Frequency Modulated)signal would be affected by the system phase error which changes in the space environment.Therefore a method of in-orbit phase pre-distortion for LFM signal based on polynomial fitting is put forward,in which the system phase error is obtained by in-orbit calibration,the phase compensation parameters are obtained by polynomial fitting on ground,and by uploading phase compensation parameters,LFM signal with compensation phase is generated by in-orbit calculation.The basis of the theory is described,as well as the realizing flow of the method is presented.Also,hardware requirements and advantages of the method are analyzed.The method is compared with other methods,and is verified to be efficient by the simulation and experiments in real system.
space-borne SAR;LFM signal;polynomial fitting;phase pre-distortion
TN958
A
0367-6234(2012)03-0137-07
2010-10-09.
孙吉利(1980—),男,助理研究员,博士研究生;
张 平(1949—),男,研究员,博士生导师;
杨汝良(1943—),男,研究员,博士生导师.
(编辑 张 宏)

