微细线切割电极丝形位误差分析

黄瑞宁，楼云江

（哈尔滨工业大学深圳研究生院，518055 深圳，huang-rn@126.com）

微细线切割电极丝形位误差分析

黄瑞宁，楼云江

（哈尔滨工业大学深圳研究生院，518055 深圳，huang-rn@126.com）

为评估电极丝在微细电火花线切割加工过程中受到各种力作用下产生偏移量大小，利用有限元方法，首先求取电极丝仅受丝张力的总体刚度矩阵和电极丝仅受放电力的总体刚度矩阵，然后结合这两个刚度矩阵推导受丝张力和放电力合力的总体刚度矩阵，利用电极丝总体刚度矩阵求出电极丝最大变形解析式，并在此基础上分析了电极丝变形的影响因素.分析结果表明:提高电极丝的张力和电极丝的刚性以及减小导丝器之间的跨度都可以减小电极丝形位误差;提供微小能量的脉冲电源使偏移量达到最小是最佳的选择.

微细电火花线切割;刚度矩阵;电极丝;形位误差

根据微细电火花线切割加工的机理可知，在加工过程中，由于受放电力、材料蚀除过程中的爆炸力、放电通道中的瞬时压力等的影响，直线切割时，电极丝会出现与进给方向相反的滞后现象，表现为电极丝发生一定程度的弯曲，如图1所示.图中T为电极丝张力，F为加工过程中电极丝受各种作用力的合力.经过大量的实验研究发现，这种电极丝在加工中出现的偏移现象对零件的表面粗糙度、几何精度有很大的影响，如果不采取措施，在拐角切割时就会形成“塌角”，严重影响加工精度［1－3］.

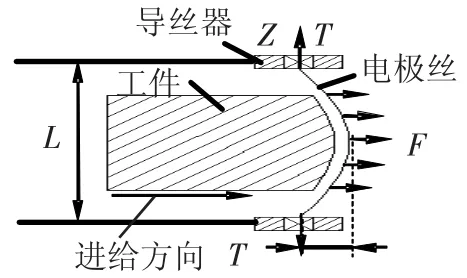
图1 微细电火花线切割加工电极丝受力示意图

由于高精度微小零件需求日益增长，使得精度成为电火花线切割加工技术未来研究热点之一，对于电火花线切割的精度问题，国内外很多学者进行了研究［4－6］.如 W.J.Hsue 等［7］在研究拐角切割效率时对拐角切割电极丝变形进行了分析，采用指数方程对电极丝运动轨迹进行了模拟.A.B.Puri等［8］对拐角切割进行了几何精度分析及优化.J.A.Sanchez等［9］对拐角切割进行了实验及数值分析.F.Han等［10］利用计算机仿真分析了静电力对加工精度的影响.而M.Yan等［11］研究通过实时控制电极丝张力来提高微细线切割加工的几何精度.上述研究都是为了提高线切割加工精度，但却没有对引起加工误差主要原因——电极丝偏移给出一个具体数学解析式.

微细电火花线切割加工过程中，电极丝轴向匀速运动，可以认为轴向动态力为零.因此在垂直于电极丝方向上(进给方向)的力则是引起电极丝偏移的主要作用力.理论上，由于采用脉冲电源进行加工，脉宽、脉间期间电极丝上的力F是交互作用的，这将引起电极丝在加工过程中发生振动，但是在放电间隙中由于阻尼很大，使得丝的振幅很小，所以可以认为在横向上(垂直于进给方向)的力是静态自平衡的.因此本文利用有限元方法分析电极丝受力变形，推导出电极丝偏移的具体数学解析式，并给出具体算例.

1 电极丝仅受丝张力的总体刚度矩阵

假定电极丝的横截面积为A，弹性模量为E，长度为L.局部轴向坐标为，局部纵向坐标为.节点自由度为局部轴向位移，即沿电极丝长度的纵向位移，用单元端部的1x和2x表示，如图2所示.

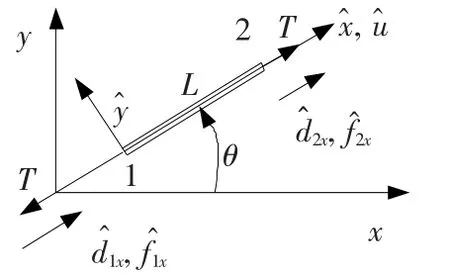
图2 受丝张力作用的电极丝单元

首先将电极丝每端的节点编号并编上单元代号代表一个单元，如图2所示.因为指定端点的线性函数有着唯一的路径，所以位移沿电极丝的轴线性变化.图3表示沿电极丝单元长度画出的线性位移函数.电极丝的方向与图2所示的方向相同.

图3 沿电极丝单元长度的位移

根据电极丝的应变εx和位移的关系、应力σx和应变εx的关系以及力的平衡原理有εx=，并可以得到

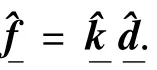
将图2所示的相对总体轴为任意方向的电极丝单元的总体节点力与总体节点位移联系起来.此关系为单元的总体刚度矩阵k，即

从式(2)看出，当使用总体坐标时，共出现4个力的分量和4个位移分量.然而，一根电极丝在局部坐标下共有2个力的分量和2个位移分量，见式(1).因此利用局部力和总体力分量之间的关系，局部位移和总体位移分量的关系可以得到总体刚度矩阵.

首先，从图4所示的广义位移矢量d，有

式中，C=cos θ，S=sin θ，下同.

图4 广义位移矢量

同时从式(3)的转换关系，可得

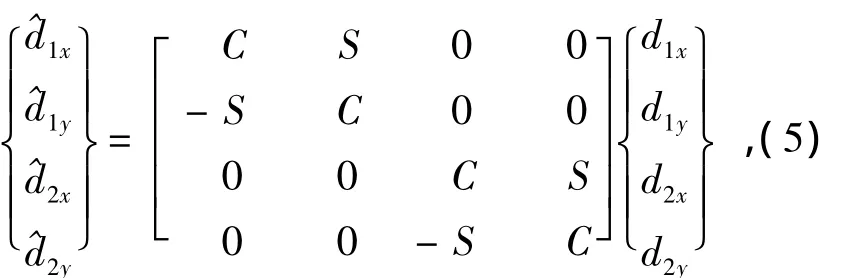
2 电极丝仅受放电力的总体刚度矩阵

图5 有正向节点的电极丝单元

假定沿单元长度纵向位移的变化为由于总共有4个自由度(每一点有1个纵向位移iy和1个小转角i)，所以式(9)表示的完全立方位移函数是适当的.此外，立方函数也满足两个单元共享节点处的位移和斜率连续条件.

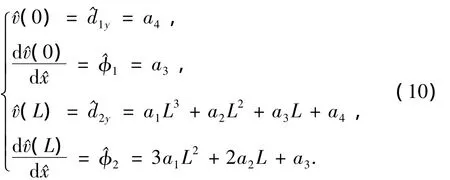
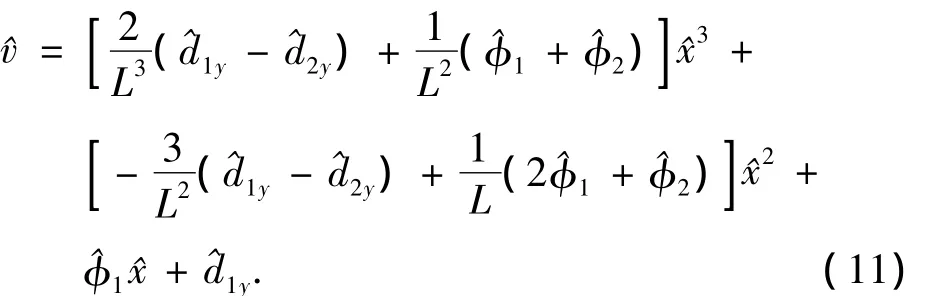
因为弯矩和剪力是与纵向位移函数相关的，即

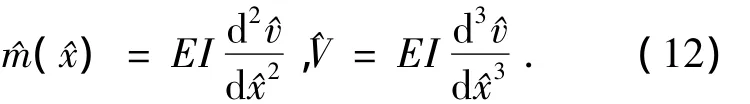
因此将式(11)和式(12)联系在一起，得出

利用式(3)可将局部位移和总体位移联系起来，并利用式(3)中的第二个式，将局部节点自由度与总体自由度联系起来，即

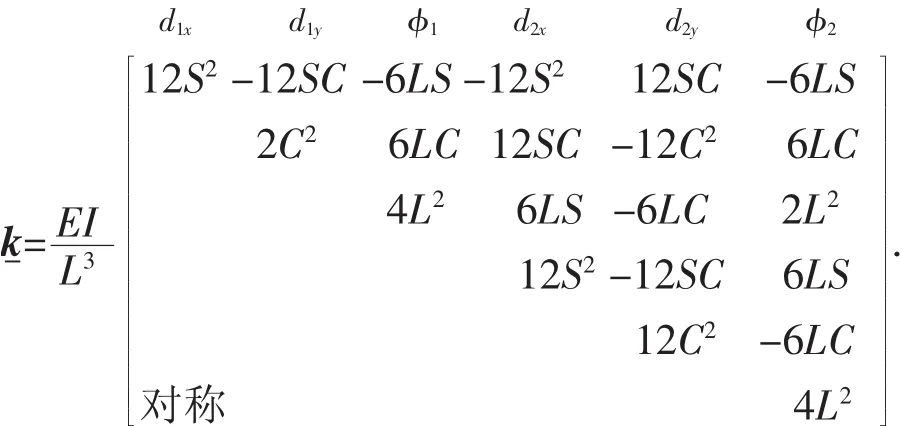
3 受丝张力和放电力合力的总体刚度矩阵

图6 电极丝单元上的局部力

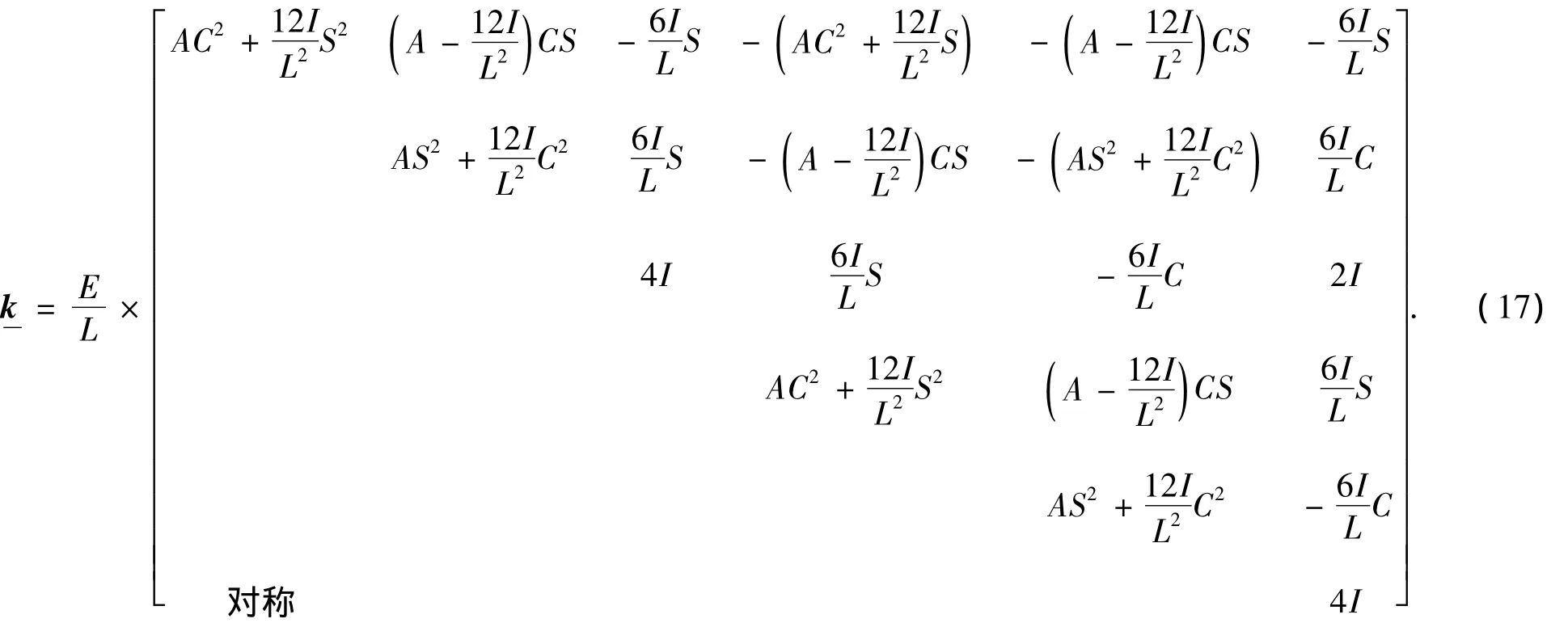
4 电极丝最大形位误差分析

电极丝在加工过程中受丝张力和放电力共同作用产生变形.假设放电力为均匀放电，利用直接刚度法计算电极丝的最大误差.从图7不难看出，电极丝最大位移在导向器的中间，即L/2处.对于分布载荷，可以用作用在节点1和节点3的力和力矩代替.

图7 电极丝受力情况

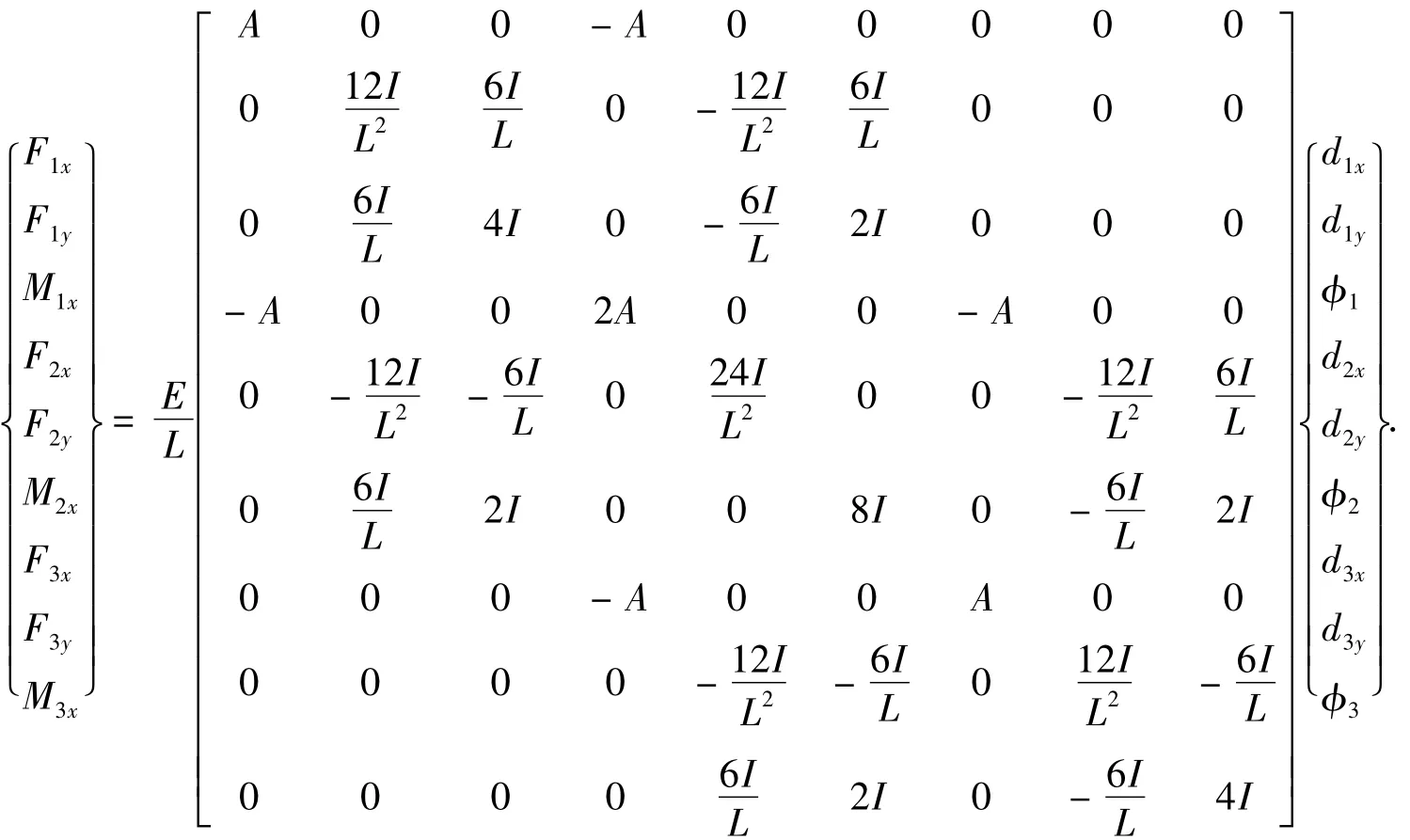
由此可得出2点的纵向位移

从图7中可以看出，电极丝偏移量与弯曲半径R和加工工件厚度L有关，并且由于电极丝的弯曲半径远远大于电极丝的偏移量，即R≫0.5d2y，有

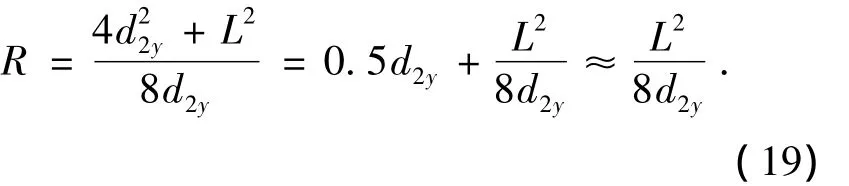
把式(19)代入式(18)，可得出电极丝的最大偏移量计算式

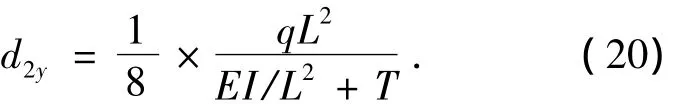
在实际应用过程中，微细电火花线切割加工多用来加工精密微细零件，一般使用直径为Φ30 μm的钨电极丝，电极丝材料的弹性模量E为38 GPa，可以计算出电极丝的惯性矩 I为3.98×10－20m4.微细电火花线切割机床的导丝器之间的跨度L为0.05 m，施加到电极丝上的张力为5 N.微细电火花线切割正常加工时，选用的脉冲宽度为 0.5 μs，脉冲间隙为 2 μs，电流为50 mA，本文假定单个脉冲的放电作用力的合力q为0.05 N.把上述参数代入式(20)，可以得到电极丝最大偏移量为

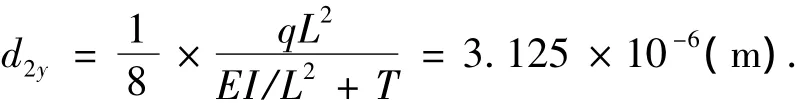
从上述计算可以看出，电极丝在加工中发生的偏移量随着丝张力的增加而降低;放电作用力和导丝器之间的跨度的增加会明显增加电极丝的偏移量.而影响最明显的为导丝器之间的跨度，跨度越大偏移量越大.其次为电极丝的张力和单个脉冲放电力合力，放电力合力越大偏移量越大，而电极丝张力越大偏移量越小.虽然电极丝的刚度(弹性模量与惯性矩的乘积为电极丝的刚度表现)并没有对偏移量大小产生很大影响，但是电极丝刚度大则可以施加更大的张力，因此也间接减小偏移量.

5 结论

1)提高电极丝的张力也是减小偏移量的途径，因此一般在电极丝刚度前提下将张力设得尽量大，而且还要对电极丝张力进行实时的检测与控制，其目的就是为了尽量减小电极丝在加工过程中的偏移量.

2)提高电极丝的刚性，能够间接减小电极丝的偏移量.因此在综合考虑的情况下，采用微细钨丝是最理想的选择.

3)减小导丝器之间的跨度，会减小电极丝的偏移量，但是跨度由工件厚度决定，因此在机床设计时，应考虑跨度能根据工件要求而改变.

4)通过电火花线切割加工材料蚀除机理不难理解，单个脉冲放电能量的增加会显著提高加工过程中产生的放电力，因此会增加电极丝的偏移量.

5)针对电极丝直径小、质量轻的特点，为了减小形位误差，提高加工精度，提供微小能量的脉冲电源来使偏移量达到最小是最佳的选择.

［1］狄士春，黄瑞宁，迟关心，等.微细电火花线切割加工关键技术［J］.机械工程学报，2006，42(1):221－226.

［2］HUANG R N，DI S C，CHI G X，et al.Development of MWEDM platform and its applications［J］.Transactions of Nonferrous Metals Society of China，2005，15(S3):268－273.

［3］HUANG R N，LOU Y J，CHI G X.Research on servo feeding system of micro WEDM［C］//ICDMA 2010，(Ⅱ).Changsha:IEEE Computer society，2010:271－274.

［4］HO K H，NEWMAN S T，RAHIMIFARD S，et al.State of the art in wire electrical machining(WEDM)［J］.International Journal of Machine Tools and Manufacture，2004，44(12/13):1247 －1259.

［5］ABBAS N M，SOLOMON D G，BAHARI M F.A review on current research trends in electrical discharge machining(EDM)［J］.International Journal of Machine Tools and Manufacture，2007，47(7/8):1214 －1228.

［6］HO K H，NEWMAN S T.State of the Art Electrical Discharge Machining(EDM)［J］.International Journal of Machine Tools and Manufacture，2003，43(13):1287－1300.

［7］HSUE W J，LIAO Y S，LU S S.Fundamental heometry analysis of wire electrical discharge machining in corner cutting［J］.International Journal of Machine Tools and Manufacture，1999，39(4):651－667.

［8］PURI A B，BHATTACHARYYA B.An analysis and optimization of the geometrical inaccuracy due to wire lag phenomenon in WEDM［J］.International Journal of Machine Tools＆ Manufacture，2003，43(8):151－159.

［9］SANCHEZ J A，PLAZA S，ORTEGA N，et al.Experimental and numerical study of angular error in wire-EDM taper-cutting［J］.International Journal of Machine Tools and Manufacture，2008，48(12/13):1420－1428.

［10］HAN F，KUNIEDA M，SENDAI T，et al.Simulation on influence of electrostatic force on machining characteristics in WEDM［J］.International Journal of Electrical Machining，2002(7):31 －36.

［11］YAN M，HUANG P.Accuracy improvement of wire-EDM by real-time wire tension control［J］.International Journal of Machine Tools and Manufacture，2004，44(7/8):807－814.

Analysis of wire electrode shape and position error of MWEDM

HUANG Rui-ning，LOU Yun-jiang

(Harbin Institute of Technology Shenzhen Graduate School，518055 Shenzhen，China，huang-rn@126.com)

During the micro wire electrical discharge machining(MWEDM)，the micro wire electrode will deform under all kinds of force.A finite element analysis approach is presented for calculating the wire electrode deform.At first，the wire's stiffness matrix only by wire tension and that only by spark force were obtained independently，and then the total stiffness matrix and the wire max deform analytic expression were got and the influential factors were analyzed.The results show that the wire deformation can be reduced by increasing the wire tension and the wire rigidity，and decreasing the span between the guide pulleys，while providing the micro energy pulse power is the best choice.

MWEDM;stiffness matrix;wire electrode;shape and position error

TG661

A

0367－6234(2012)03－0069－06

2011－01－03.

国家自然科学基金资助项目(51105110);哈尔滨工业大学创新基金资助项目(HIT.NSFIR.2010125);高等学校博士学科点专项科研基金资助项目(20112302120075).

黄瑞宁(1977—)，男，博士，讲师.

(编辑 杨 波)