一类微分代数捕食-食饵系统的离散化及其定性分析

吴雪莹,陈伯山,宣天赐,王桂臻

(湖北师范学院 数学与统计学院,湖北 黄石 435002)

0 引言

在生态动力系统中，捕食-食饵系统受到了数学工作者们的广泛的深入的研究。其中Lotka-Volterra捕食-食饵模型在捕捞业以及生态管理中广泛应用，具有重要的生态意义。

1 模型的建立

本文基于一个Lotka-Volterra捕食-食饵系统和1954年Gordon提出的捕捞经济理论[14]，考虑了捕捞捕食者种群的捕捞行为对模型的影响，建立了如下由微分代数方程描述的捕食-食饵模型：

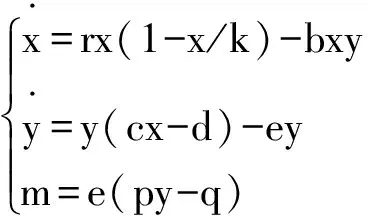
(1)

其中x(t)和y(t)分别表示食饵种群和捕食者种群在时刻t的数量，k是食饵种群的容纳量，r是食饵种群的固有增长速度，bx是捕食者的功能性反应，c是食饵向捕食者转化的速率，d是捕食者种群的死亡率，e是捕捞的捕食者种群数量，p是被捕捞的单位重量捕食者的售价，q是单位重量捕食者的捕捞成本，m是单位捕捞成果带来的的经济利益。

首先我们进行无量纲变换，将系统 (1)简化为：

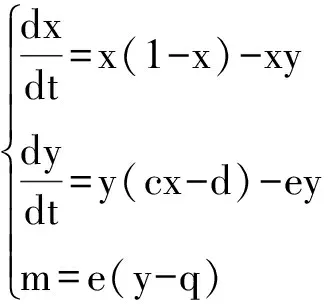
(2)

然后我们利用庞克莱方法对系统(2) 进行离散化，得到了下面的离散奇异系统：

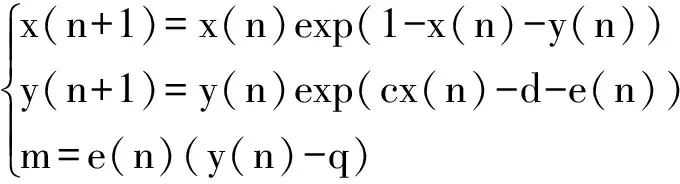
(3)

简记为下列形式：

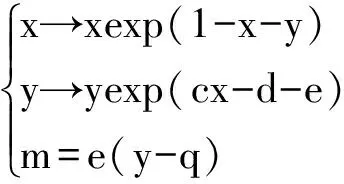
(4)

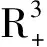
本文将对离散奇异系统 (4)进行定性研究。首先通过运用微分代数系统理论与分支理论讨论模型的平衡点的局部稳定性和分支问题，证明Neimark-Sacker分支的存在性；接着选取捕捞行为的经济利益m作为分支参数，研究Neimark-Sacker分支及其方向；最后通过matlab数值模拟验证结果的正确性和合理性。

2 平衡点的稳定性分析

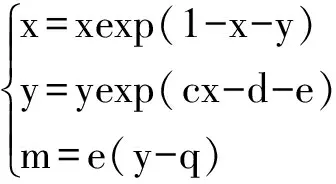
可得一个关于e的一元二次方程

e2+(d+cq-c)e+cm=0

(5)

方程(5)的判别式为△=(c-d-cq)2-4cmh2-4cm，其中h=c-d-cq.

为保证系统(4)具有实际意义，在本文中我们只考虑系统参数在

范围内变化。

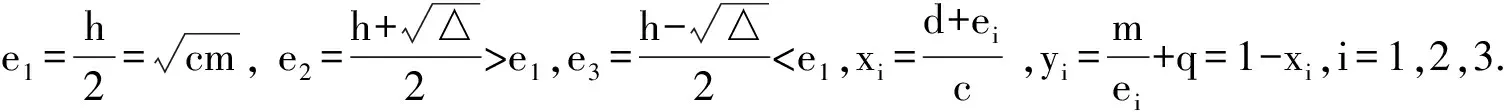
然后我们来研究正平衡点的局部稳定性。先求出系统(4) 在平衡点E(x,y,e) 处的雅可比矩阵为

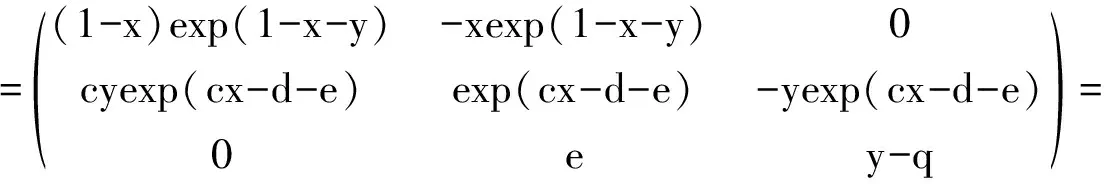
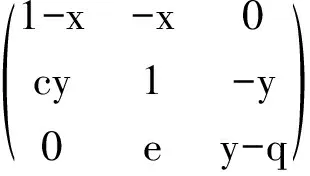
那么J(E) 的相应的特征方程为

λ2+Pλ+Q=0

(6)

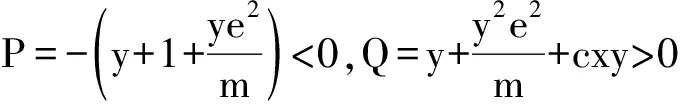
对于特征方程(6)，令F(λ)=λ2+Pλ+Q，则

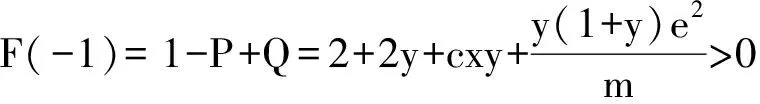
经过分析，我们得到离散奇异系统 (4)的平衡点的局部稳定性定理如下。

定理2 当△=0时，系统(4)有唯一非双曲的正平衡点E1.当△>0时，系统(4) 有两个正平衡点E2和E3，其中E2为鞍点，E3为

1) 汇当且仅当Q3<1；

2) 源当且仅当Q3>1；

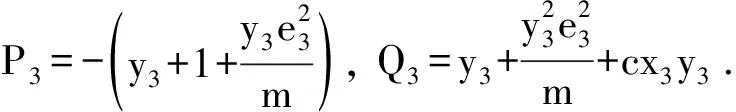
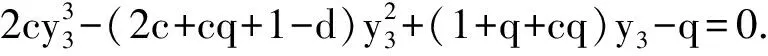
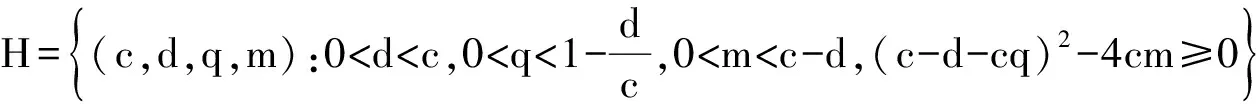
的适当的参数值c，d，q，便可以求出该一元三次方程的根，进而找到相应的m值，记为m0.

从上面的分析我们可以得到：

当m在m=m0的小邻域内变化并且 (c,d,q,m)∈H∩M时，系统 (4)在正平衡点E3处会出现Neimark-Sacker分支，其中

M={(c,d,q,m):P2-4Q=g(c,d,q,m)<0,m=m0}

3 正平衡点E3处的Neimark-Sacker分支分析

选取系统参数 (c,d,q,m0)∈H∩M，系统 (4)即为

(7)

且E3(x3,y3,e3)是系统(7) 的一个正平衡点。 选取m*作为一个分支参数，系统(7) 在微小扰动下变为

(8)

其中|m*|≪1 ，为一个很小的扰动参数。

通过运用中心流形定理和微分代数系统理论，系统 (8)可简化为

(9)

其中

a1=1-x3,a2=-x3,a11=x3-2,a12=x3-1,a22=x3

a111=3-x3,a112=2-x3,a122=1-x3,a222=-x3

系统 (9)在Z(z1,z2)=(0,0)处的线性化系统的特征方程为

λ2+P(m*)λ+Q(m*)=0

且x3,y3，e3的表达式中的m都替换为m0+m*.因此

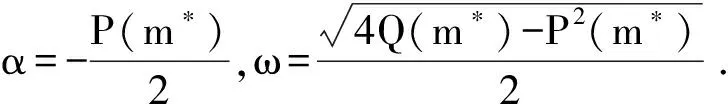
通过分析计算可得系统(9) 在m*=0 处的范式为

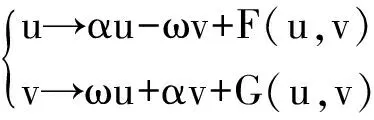
(10)

系统(10) 中的F(u,v) 和G(u,v) 为

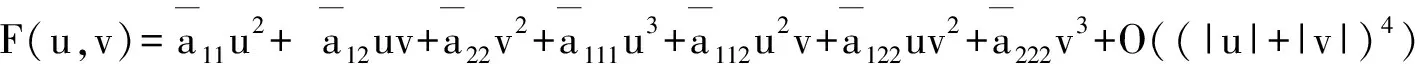
其中

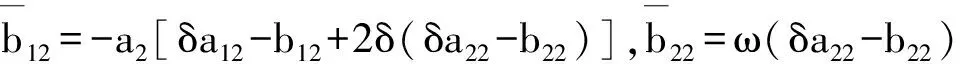
由F(u,v)和G(u,v)可计算其在(0,0) 处的二阶、三阶导数为

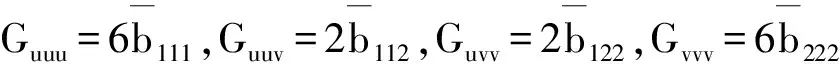
为了使系统(10) 存在Neimark-Sacker分支，要求下面的判定值不为零：

(11)

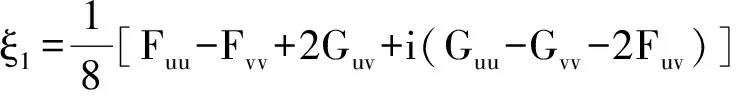
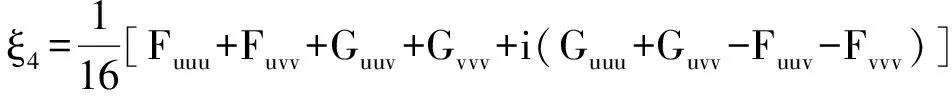
由以上分析和Neimark-Sacker分支理论，我们有以下结论：

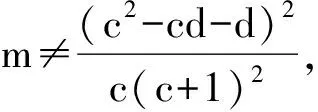
1) 当β<0 时，若m>m0， 则E3是不稳定的平衡点且有一个渐进稳定的周期轨道；若m

2) 当β>0 时，若m>m0，则E3是不稳定的平衡点且无周期轨道；若m

4 例子验证

例 我们令c=1，d=0.1，q=0.1，根据上述分析可求得分支值m0=0.01，并满足(c,d,q,m0)=(1,0.1,0.1,0.01)∈H∩M，此时系统(4) 有两个正平衡点E2和E3，且当参数m在m0=0.01的小邻域内变化时，系统(4) 在正平衡点E3(x3,y3,e3)处存在Neimark-Sacker分支。此时计算得特征值为λ±=0.9508±i0.3098，|λ±| =1，β=-0.4266<0.因此若m>m0，E3是不稳定的平衡点且有一个渐进稳定的周期轨道；若m

图1 当c=1,d=0.1,q=0.1,m=0.01-0.008时的N-S分支图

在图1中，m=0.01-0.008，正平衡点(0.1025,0.8975,0.0025) 是稳定的。

图2 当c=1,d=0.1,q=0.1,m=0.01+0.008时的N-S分支图

在图2中，m=0.01+0.008 ，正平衡点(0.1025,0.8975,0.0025) 是不稳定的。

图3 当c=1,d=0.1,q=0.1,m=0.01+0.0001时的N-S分支图

在图3中，m=0.01+0.0001在m=0.01的小邻域内，在平衡点(0.1025,0.8975,0.0025)处产生一个渐进稳定的周期轨道。

参考文献：

[1]陈伯山, 刘永清.非线性微分代数系统的稳定性[J].控制理论与应用,2000, 17(1), 40～44.

[2]陈伯山, 廖晓昕.微分代数系统的标准型和分支[J].应用数学学报, 2000, 23(3), 429～443.

[3]He Zhimin, Lai Xin.Bifurcation and chaotic behavior of a discrete-time predator-prey system[J].Nonlinear Analysis: Real World Applications, 2011, 12: 403～417.

[4]Jing Zhujun, Yang Jianping.Bifurcation and chaos in discrete-time predator-prey system[J].Chaos, Solitons and Fractals, 2006, 27:259～277.

[5]Liu Xiaoli, Xiao Dongmei.Complex dynamic behaviors of a discrete-time predator-prey system[J].Chaos, Solitons and Fractals, 2007, 32:80～94.

[6]Fazly Mostafa.Hesaaraki Mahmoud.Periodic solutions for a discrete time predator-prey system with monotone functional responses[J].C R Acad Sci Paris, Ser I, 2007, 345:199～202.

[7]Yang Wensheng, Li Xuepeng.Permanence for a delayed discrete ratio-dependent predator-prey model with monotonic functional responses[J].Nonlinear Analysis: Real World Applications, 2009,10:1068～1072.

[8]Hu Zengyun, Teng Zhidong, Zhang Long.Stability and bifurcation analysis of a discrete predator-prey model with nonmonotonic functional response.Nonlinear Analysis: Real World Applications, 2011, 12:2356～2377.

[9]Xia Yonghui, Cao Jinde, Lin Muren.Discrete-time analogues of predator-prey models with monotonic or nonmonotonic functional responses.Nonlinear Analysis: Real World Applications, 2007, 8:1079～1095.

[10]Liu Chao, Zhang Qingling, Wang Jixin.Dynamics and control in a differential-algebraic prey-predator model[C].Chinese Control and Decision Conference, 2009,2: 3052～3057.

[11]Zhang Guodong, Zhu Lulu, Chen Boshan.Hopf bifurcation and stability for a differential-algebraic biological economic system[J].Applied Mathematics and Computation, 2010,217:330～338.

[12]Chakraborty Kunal, Chakraborty Milon, Kar T K.Bifurcation and control of a bioeconomic model of a prey-predator system with a time delay[J].Nonlinear Analysis: Hybrid Systems, 2011, 5: 613～625.

[13]Liu Chao, Zhang Qingling, Zhang Xue, et al.Dynamical behavior in a stage-structured differential-algebraic prey-predator model with discrete time delay and harvesting[J].Journal of Computational and Applied Mathematics, 2009, 231:612～625.

[14]邹德新, 刘 超.具有阶段结构的广义食饵-捕食者系统的分岔及控制[J].生物数学学报, 2009, 24(4):711～720.

[15]Bru Rafael, Coll Carmen, Sánchez Elena.Structural properties of positive linear time-invariant difference-algebraic equations[J].Linear Algebra and its Applications, 2002, 349:1～10.