一类二维差分方程中的混沌现象

戴华炜,程晓胜

(惠州学院 数学系，广东 惠州 516007)

0 引言

在某一些非线性差分方程中，存在着一种有趣的现象——混沌现象。第一个混沌模型是20世纪70年代初美国气象学家Lorenz发现的，之后，混沌现象便引起了学者们的极大关注和研究兴趣。虽然，混沌还没有一个公认的普遍适用的定义，但一般地，将发生在确定性系统中的貌似随机的不规则运动称为混沌[1]，混沌系统具有对初值的敏感性的特征。

差分方程在经济领域、动力系统和生态系统等多方面都有广泛应用[2]。二维差分方程起着从一维到高维的衔接作用，对二维差分方程的混沌研究有助于认识和预测更复杂的高维动力学系统的性态[3]。因而, 对二维差分方程中混沌现象的研究不论在理论上还是在实际应用上都具有重要的意义。

本文将研究一个二维差分方程——宿主-寄生物模型，利用分岔图、 Lyapunov 指数图、时间序列图和相图分析该方程由周期运动到混沌运动的变化过程，研究该方程的混沌现象。

1 二维差分方程——宿主-寄生物模型

生态系统中对于单种群模型已有不少研究，而对种间相互作用的种群模型的研究主要集中在含有两个变量的时间连续的相互作用的Lotka-Volterra种群模型，但Nicholson与Bailey认为Lotka-Volterra种群模型没有考虑种内竞争效应，不适用于离散世代物种，于是建立了以宿主-寄生蜂系统为对象的Nicholson- Bailey模型。种群生态学家又改进Nicholson- Bailey模型，提出了各种离散世代的宿主-寄生物模型[4]。

本文所要研究的二维差分方程如下：

(1)

其中，Nt,Pt分别为宿主和寄生物在世代t的种群个体数；Nt+1,Pt+1分别为宿主和寄生物在世代t+1的种群个体数；r为宿主的内禀增长率；a为寄生物的搜寻效率；K为环境容纳量。

该二维差分方程为各种离散世代的宿主-寄生物模型中的一种，是生态学中一个重要的数学模型。它考虑了种群密度对种群规模增长的影响，且宿主与寄生物随机相遇，搜寻效率与每个寄生者单位时间遇到的宿主成正比例关系。该方程形式较复杂，其动力学行为由参数r，K，a决定。

2 分岔图

为了研究二维差分方程(1)中的混沌现象，可以利用分岔图。方程的分岔图就是以变化的参数为横坐标，方程迭代的极限为纵坐标所作的图。这样得到的图形能够观察出方程不动点、周期点随参数的变化情况。我们选取r=3，K=1来观察a的变化对系统动态的影响。使用MATLAB编程，初始点在[0,1]间随意取值，为保证计算时方程的轨道已收敛到吸引子上，让方程 (1) 迭代1000次，再绘制最后10个点，图1是方程(1)以a为参数在区间[2，6]关于N，P的分岔图。从图1可以看出，图像在a∈[2,3.22]时为一段曲线，则方程在a∈[2,3.22]时收敛，宿主与寄生物稳定共存；方程在a=3.23时出现Hopf分支，在a∈[3.23,3.62]时做概周期运动；图像在a∈[3.63,3.90]时突然变为四段曲线，即方程出现4周期运动；方程在a>3.91时，随着a的增大，开始没有规律性，方程逐渐进入混沌。

图1 2≤a≤6范围关于N，P的分岔图

3 Lyapunov 指数

Lyapunov 指数是目前在表征混沌运动方面显示出重大意义的统计特征量之一，它是用来度量相空间中两条相邻的轨迹随时间变化按指数规律吸引或分离的程度，指数的正负可以表征系统运动的特征。正的Lyapunov指数对应本征矢方向上的位移初始点,其发展出来的轨道会呈指数化分离趋势；在负的Lyapunov指数对应本征矢方向上,相空间轨道会相互吸引趋近。因此,在非线性动力系统的研究中经常将正的Lyapunov指数作为混沌是否出现的一个判据。

对于离散系统，Rn空间上的差分方程

xn+1=f(xn)xn∈Rn

(2)

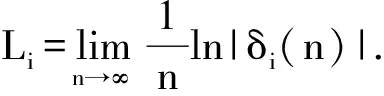
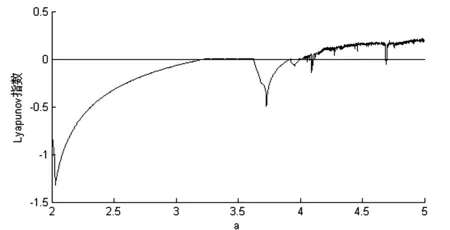
图2 2≤a≤5范围的Lyapunov指数图

从图2中可见，当a>4.04时，Lyapunov 指数大于零，这说明方程进入混沌现象。图2 验证了该二维差分方程的Lyapunov 指数图与分岔图吻合，该方程随参数a在区间[2，6]的变化表现出丰富的动力学行为。

4 时间序列图和相图

分岔图和Lyapunov指数图从总体上反映了方程(1)从收敛到混沌的整个变化过程，而从方程的时间序列图和相图中，可以具体了解方程(1)从收敛到混沌的变化过程[7]。时间序列图是以迭代次数为横坐标，方程每次迭代的值为纵坐标所作的图。相图是分别以两个变量为横坐标，纵坐标，作出方程迭代轨迹的图。时间序列图和相图是研究混沌现象的一个有用的工具。图3～5是参数a分别等于3，3.4，5时关于N的时间序列图及相图。

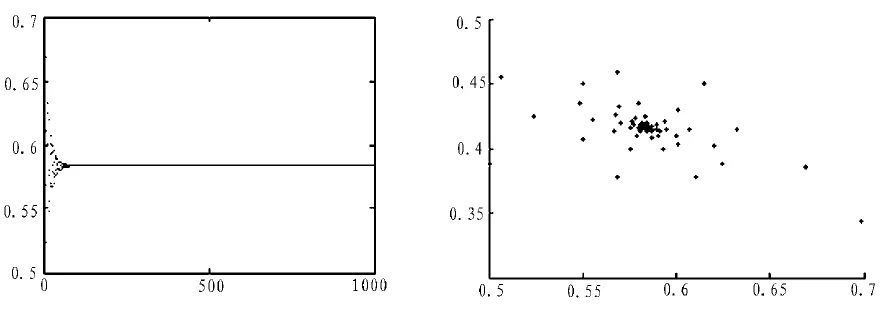
图3 a=3时关于N的时间序列图及相图

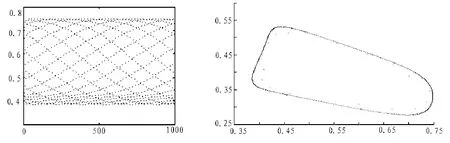
图4 a=3.4时关于N的时间序列图及相图

图5a=5时关于N的时间序列图及相图

从图3～5可看出，当a=3时，方程振荡地收敛于一个平衡点，说明宿主与寄生物稳定共存。当a=3.4时，方程出现极限环。当a=5时，方程的时间序列图与相图都是一片混乱，没有规律，这说明了方程处于混沌状态。

5 混沌现象

根据以上分析，二维差分方程(1)在r=3，K=1，a>4.04时逐渐进入混沌。混沌是由确定性系统产生的貌似随机的现象。一般认为混沌现象有如下几个特征[8]:

1)遍历性。当方程处于混沌状态时，方程迭代的极限值是取遍整个区间的。从图5可以看出当a=5时，方程(1)的N值取遍了区间[0，2.5]，P值取遍了区间[0，0.9].

2)非周期运动性。当方程处于混沌状态时，方程的运动是非周期的。从图3～4可以看出，当方程不是处于混沌状态时，它的运动是有周期性的，而从图5看出，当方程处于混沌状态时，它的运动呈现一片混乱，没有周期。

3)初值的敏感性。当方程处于混沌状态时，不管初值取值多么接近，最终迭代的结果却会相差极大。

对初始条件的敏感性是混沌现象的一个典型特征，正是这一特征使得具有混沌现象的模型，明明是确定的系统，却无法预知结果。

通过MATLAB编程，分别作出当a=3，a=5时在初值取(0.5，0.5)与(0.50001，0.50001)时迭代200次后结果的误差图。图6a，6b为所作的图。

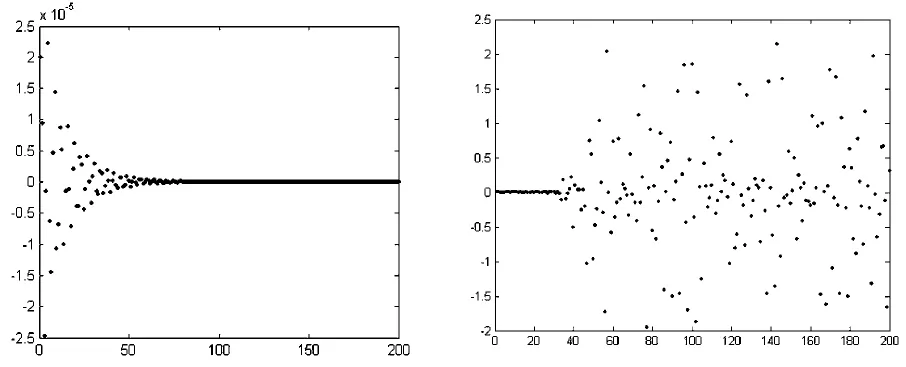
图6aa=3时，初值分别取(0.5，0.5)与(0.50001，0.50001)时迭代200次结果的误差图 图6ba=5时，初值分别取(0.5，0.5)与(0.50001，0.50001)时迭代200次结果的误差图

从图6可以看出，当a=3时，即方程收敛时，初值差距0.0001的迭代结果的差距也几乎为0.当a=5时，即方程处于混沌状态时，初值差距0.0001的迭代结果的差距却极大，有的甚至可以相差高达2.

混沌现象是非线性动力系统的固有特性，是非线性系统普遍存在的现象，它广泛存在于现实生活和实际工程技术问题中。对混沌现象的研究是极其必要的，它有助于我们更加了解生活中看似无规律的现象。混沌现象表明我们无法对系统的长期行为进行预测，但是混沌现象中还是存在着规律的，因此可以利用混沌中的规律对系统进行短期的行为预测。

6 小结

本文研究了一个二维差分方程，且该方程为宿主-寄生物模型。通过MATLAB编程，先作出了该方程的分岔图，找出参数在什么范围时，方程出现收敛、周期和混沌。再结合 Lyapunov 指数图从总体上分析了方程从收敛到混沌的整个变化过程，分析结果与分岔图的分析结果吻合。接着利用时间序列图和相图，具体了解方程从收敛到混沌的过程。分析发现该方程随着参数的变化表现出丰富的动力学行为，也研究了该方程的混沌现象，研究表明混沌现象具有遍历性、非周期运动性、初值敏感性的特征。

参考文献：

[1]王兴元.复杂非线性系统的混沌[M].北京:电子工业出版社,2003.

[2]邓志颖,潘建辉,沈世云.差分方程在数学模型中的应用[J].科技信息,2011,(20):432～435.

[3]谢艳云,常迎香,孙 海，等.二维系统的分岔行为及混沌控制[J].吉首大学学报(自然科学版) ,2006,27(05):27～30.

[4]刘 华,李自珍,刘志广,等.宿主-寄生物种群模型的复杂动态[J].兰州大学学报(自然科学版),2009,45(04):53～59.

[5]勇 俊,郭丽华,吴兴波,等.MATLAB在研究非线性混沌中的应用[J].吉林化工学院学报, 2003,20(02):41～43.

[6]王云雄,翁贻方,郑德玲.混沌的复杂度研究方法和Logistic映射分析[J].北京工商大学学报(自然科学版), 2006,24(02):38～41.

[7]于万波.混沌的计算实验与分析[M].北京:科学出版社,2008.

[8]朱永松.基于Matlab一类混沌模型的研究与实现[J].湖北工业大学学报,2006,21(01):25～27.