基于分形理论的自动舵液压阀故障诊断方法研究

李天伟 ， 樊明波 ， 黄 谦 ，3， 李正友 ，4

（1.海军大连舰艇学院航海系，辽宁 大连 116018；2.镇江船艇学院，江苏 镇江 230013；3.海军91257部队，浙江 舟山 316001；4.解放军69029部队，新疆 乌鲁木齐 830011）

0 引 言

自动舵液压阀在其运行过程中必然产生振动，液压阀状态的改变将影响测得的振动信号，振动信号里包含了丰富的液压阀状态信号。当液压阀出现油液污染、弹簧失效或阀芯磨损等问题时，将影响其正常换向，导致自动舵出现故障。液压阀发生故障时，其振动信号突出表现为振动的非平稳和非线性。传统的液压设备诊断技术是针对振动信号的时域或频域特征来提取特征量进行故障识别。实际上在不同的故障状态下，其非线性因素的影响是不同的；因此，如何准确地刻画液压阀故障状态对液压阀的故障诊断是很有帮助的。

分形与混沌理论是当今非线性科学研究的一个重要且非常活跃的方面，它特别适合于各种“复杂现象”。分形理论中分形维数是定量刻画混沌吸引子的一个重要参数，广泛应用于非线性行为的定量描述中[1]。在设备故障诊断领域中，研究人员开始用分形维数对所测取的信号进行分析，并取得了一定的成果[2-4]。利用分形理论，不仅可以定性地分析系统的运动状态，还可以通过计算与其唯一对应的分形维数对其运动状态进行量化，从而实现对液压设备的故障诊断。关联维数作为分形维数的一种，对吸引子的均匀性反应敏感，更能反映吸引子的动态结构，只要捕捉到分形维数的变化情况，便可以对液压设备故障作出诊断。

1 分形特征量计算

分形维数有很多种，本文选取了关联维数作为分形维数实现对液压阀的故障诊断，同时，依据液压阀阀芯位移信号的特点，选取从时间序列计算关联维数的G-P算法进行分形维数计算。

1.1 G-P算法

为了能够从一维时间序列中得到动力系统相空间的几何结构，Packard等人采用时间延迟技术重构相空间。1983年，Grassberger和Procaccia根据嵌入理论和重构相空间思想，提出了从时间序列直接计算关联维数D2的算法，即G-P算法[1]。

长度为N的序列用时延法可以构成长度为Nm、维数为m的相空间。重构相空间的维数m称为嵌入维数。设原始信号时间序列为{x1，x2，…，xN}，重构的伪相空间轨道为

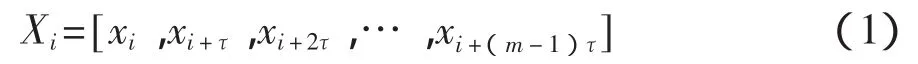
式中：τ——时间延迟；

i=1，2，…，Nm，Nm=N-（m-1）τ是重构相空间中向量的个数。

吸引子关联维数由式（2）相关积分导出

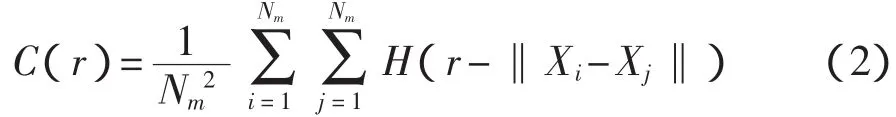
式中：i≠j；

C（r）——信号的相关积分（关联函数）；

H——Heaviside函数，当u≥0时，H（u）=1，当u＜0 时，H（u）=0；

r——相空间中超球半径。

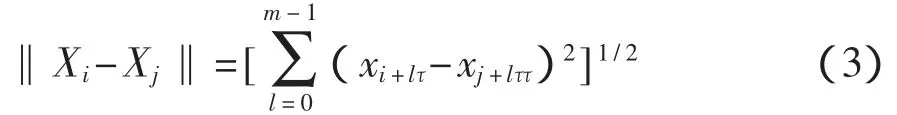
相关积分C（r）含义是嵌入空间中距离≤r的向量对出现的概率，且有

式中：D2——关联维数，可由式（5）求出

1.2 参数的选取

1.2.1 延迟时间的选取

实际运用中延迟时间τ的选取对重构质量的好坏有极大影响。如果 τ太小，相空间 xn+jτ和 xn+（j+1）τ的坐标差别极小，运动轨迹总是在对角线附近，携带了大量的冗余信息；反之τ太大，坐标之间又变得独立无关，特别是对于非线性混沌运动，任何微小的差异都会随时间演化而越来越大，从而使得前后状态完全无关[5]。在时间序列相空间重构中，延迟时间的算法主要有自相关函数法和互信息法两大类。

1.2.2 嵌入维数的选择

在重构相空间时，Takens定理提供了嵌入维数m的下限，即嵌入维数m≥2d+1（其中d为吸引子的真实维数）。由于无法获得吸引子的真实维数，嵌入维数的下限也很难得出；因此，在研究中应尽量选择大的嵌入维数，以满足m≥2d+1。但嵌入维数过大，会增加计算量，且多余的相空间维数会放大原时间序列中噪声的效应；而嵌入维数太小，动力系统的几何结构不能完全打开。现有的许多选择m的方法，如奇异值分解[6]、伪相图法[7]等，其各有利弊。

1.2.3 超球半径的选择

超球半径r的取值范围首先应满足条件：

式中：lmin=min（‖Xi-Xj‖）；

lmax=max（‖Xi-Xj‖）；

i，j=1，2，…，Nm，i≠j。

如果r取得太大，则任何一对矢量都发生“关联”，此时C（r）=1；如果r取的太小，则任何一对矢量都不“关联”，此时C（r）=0。两种情况下的r都不能客观反映系统的内在特质，所以必须适当地选择r，使其在某个区间内满足式（4），使关联维数能客观描述自相似结构的混沌吸引子特征。

1.3 无标度区的确定

自然界大量存在的随机分形，它们只是在一定的尺度范围（即无标度区）内具有分形特性。可以采用作图法找出无标度区并计算分形维数（关联维数），如根据lnr-lnC（r）图求取信号的分维数值。此外，目前还发展了多种求取无标度区和分维数的其他算法，如三折线法[8]、遗传算法[9]和自适应方法[10]等。

2 液压阀数学模型的建立

液压阀作为自动舵的执行机构舵机的控制部分，其作用是根椐放大器输出的转舵信号控制液压油路的断通和流向，从而确定舵机液缸活塞的运动方向。

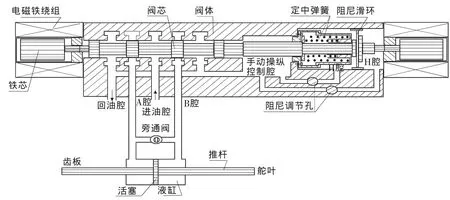
图1 CDF-100液压阀结构原理图

图1为CDF-100液压阀结构原理图，是由阀芯和阀体两部分组成的三位四通电磁换向阀。通过对液压阀的电路、磁路及受力进行分析，可建立其数学模型，有

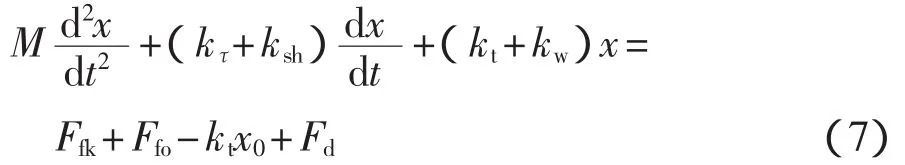
式中：M——阀芯质量；

x——阀芯位移；、

t——时间；

kτ——粘性阻尼系数；

ksh——瞬态液动力系数；

kt——弹簧刚度；

kw——稳态液动力刚度；

Ffk——卡紧摩擦力；

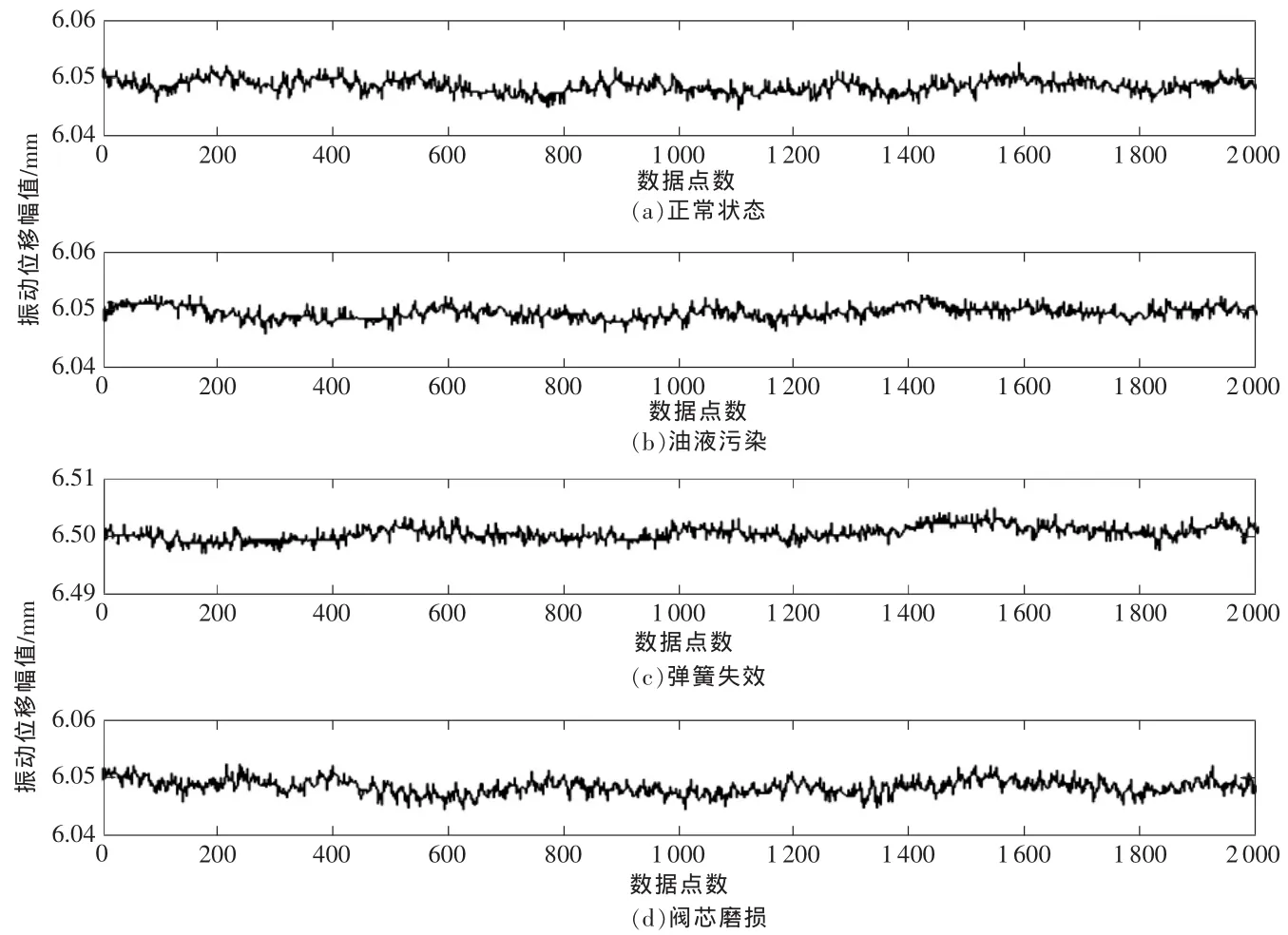
图2 液压阀4种状态下阀芯的振动信号

Ffo——O型密封圈的摩擦力；

x0——复位弹簧预压缩量；

Fd——电磁力。

3 液压阀故障诊断实例分析

使用Matlab/Simulink对CDF-100液压阀正常和3种故障（油液污染、弹簧失效和阀芯磨损）进行仿真实验，采用四阶Runger-Kutta算法，仿真步长0.0001s，仿真时间0.5 s，得到液压阀换向过程中阀芯位移振动数据5 001个点，除去前3 001个瞬态点，取后2000点进行时间序列分析，如图2所示。

图2中（a）～（d）都反映了液压阀工作过程中阀芯微动的存在，其中弹簧失效故障是指由于弹簧的失效使得阀芯的平衡位置发生改变，振动机理也有所改变，其他两个故障在平衡位置上没有发生变化，只是在振动机理上的改变。

本文采用自相关函数法来选取时间延迟τ，取自相关函数值降到初始值的1-1/e时的τ值为最佳时间延迟。如图3所示，图中与x轴平行贯穿始末的直线为初始值的1-1/e。

由图3可知，液压阀4种状态下阀芯的振动信号的最佳延迟时间τ值分别如表1所示。

对于时间序列，利用先前确定的最佳时间延迟，给定一个嵌入维数，进行相空间重构，计算其关联函数，画出关联积分曲线。在关联积分曲线图上，拟合其中线性度最好的区间，则该区间拟合直线的斜率就是该嵌入维数下的关联维数。然后增加嵌入维数，用同样的方法在关联积分曲线图上计算关联维数，直到关联维数不再随嵌入维数的增加而增加，而是在一定误差范围内变化为止，此时的关联维数就是该时间序列的关联维数。图4为不同的嵌入维数所对应的关联积分曲线，图5为关联维数随嵌入维数的变化关系，表2为关联维数随嵌入维数的变化关系的数据显示。

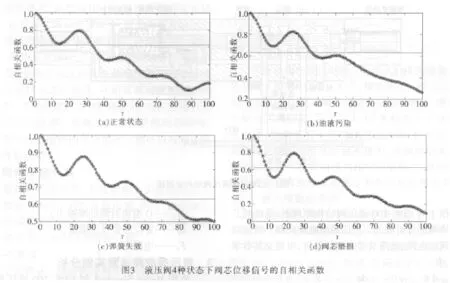
表1 液压阀4种状态下阀芯振动信号的最佳延迟时间

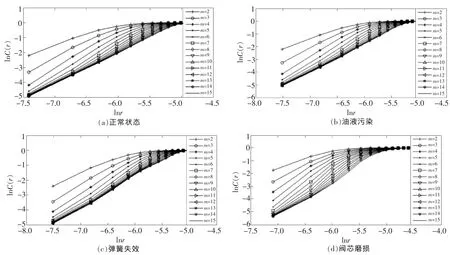
图4 液压阀4种状态下阀芯位移信号的关联积分曲线

由图5和表2可知，4种工作状态下当阀芯振动的位移信号随着嵌入维数的增加，其关联维数也增加。但当嵌入维数大于一定值时，关联维数不再随嵌入维数的增加而增加，而是在一定误差范围内变化。当嵌入维数m分别≥11，9，11和12时，关联维数分别趋于稳定值 d=2.08，2.30，2.55，3.73，满足嵌入定理m≥2d+1。分别取最小嵌入维数11，9，11和12，它标志系统有效自由度的数目，得4种工作状态下阀芯振动位移信号的关联维数2.08，2.30，2.55和3.73。可以看出，该型液压阀阀芯振动信号在一定的尺度范围内具有分形特征，不同的工作状态对应不同的分形维数，而且具有明显可分性，分形维数可以代表不同的工作状态（故障）。因此，可以把关联维数为2.08代表正常状态，2.30代表油液污染故障，2.55代表弹簧失效故障，3.73代表阀芯磨损故障。实际应用中，采集液压阀阀芯位移信号，计算其关联维数值，若关联维数值在 2.08，2.30，2.55，3.73附近时，则液压阀对应于正常状态、油液污染、弹簧失效和阀芯磨损状态。

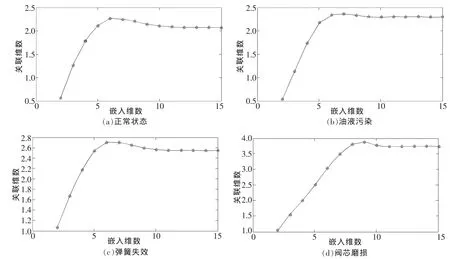
图5 关联维数随嵌入维数的变化曲线

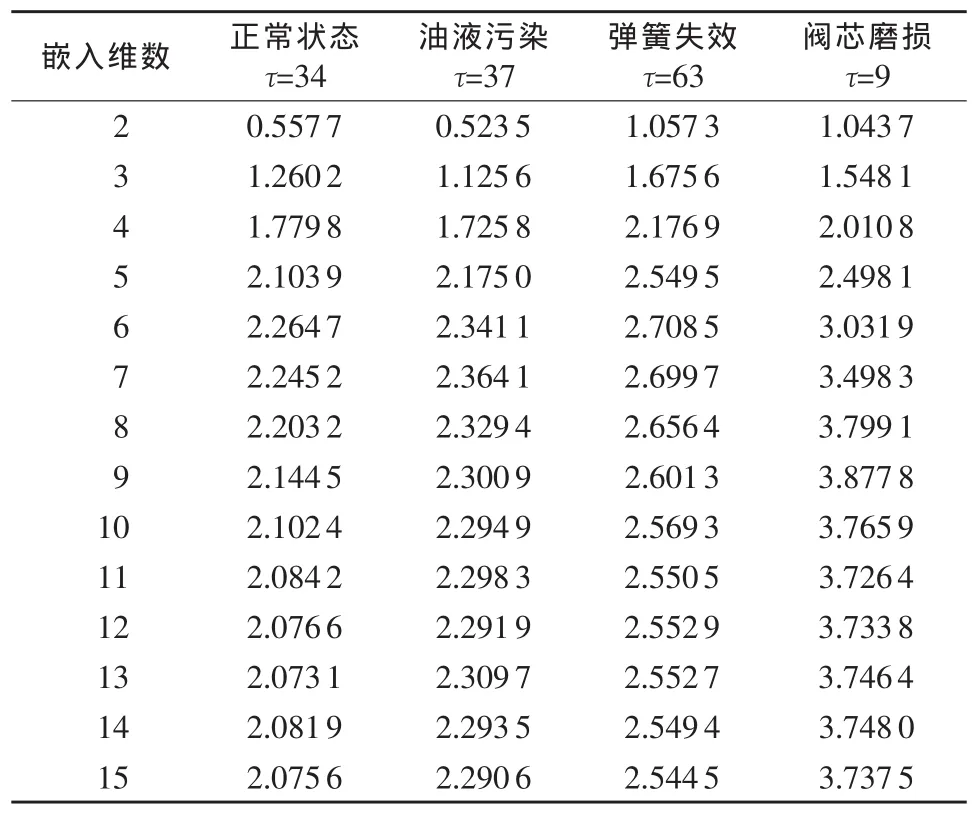
表2 不同嵌入维数下的关联维数

4 结束语

本文利用分形理论，通过计算液压阀阀芯位移信号的关联维数，对液压阀的不同工作状态进行了定量描述，并以此为依据实现了对不同液压阀故障的诊断。研究结果表明，该方法直接、简洁、方便，克服了传统方法在故障信号特征提取和分析上的困难，具有良好的实际应用价值。

[1]吕金虎，陆君安，陈士华.混沌时间序列分析及其应用[M].武汉：武汉大学出版社，2002：2-71.

[2]徐玉秀，原培新，杨文平.复杂机械故障诊断的分形与小波方法[M].北京：机械工业出版社，2003：1-45.

[3]李伟，李天伟，王桂军，等.分形特征的模拟电路故障诊断方法[J].中国测试，2010，36（2）：14-17.

[4]詹亮，刘浏.基于分形维数的火焰特征提取方法[J].西华大学学报：自然科学版，2009，28（5）：45-47.

[5]张菁，樊养余，李慧敏，等.相空间重构中延迟时间选取的新算法[J].计算物理，2011，28（3）：469-474.

[6]王浩，张来斌，王朝晖，等.迭代奇异值分解降噪与关联维数在烟气轮机故障诊断中的应用[J].中国石油大学学报，2009，33（1）：93-98.

[7]于庆江.分形方法在往复压缩机状态监测与故障诊断上的应用[D].大庆：大庆石油学院，2007：12-36.

[8]李厚强，汪富泉.分形理论及其在分子科学中的应用[M].北京：科学出版社，1997：23-68.

[9]费斌，蒋庄德，王海容.基于遗传算法求解分形无标度区的方法[J].西安交通大学学报，1998，32（7）：72-75.

[10]巫兆聪.分形分析中的无标度区确定问题[J].测绘学报，2002，31（3）：240-244.