飞行系统仿真精度的时序建模检测方法

张玉叶，王春歆，许兆林，周胜明

（1.海军航空工程学院青岛分院，山东 青岛 266041；2.北海舰队，山东 青岛 266001）

0 引 言

为降低飞行试验在飞机研制中的成本耗费，虚拟仿真试验成为重要的替代手段。仿真试验通过接收飞机的控制参数和环境参数，解算出飞机的飞行数据，进而可以测试飞机的各项性能参数。其前提是仿真系统正确可靠，所以需要对仿真数据的稳定性及精度进行检验，时间序列建模分析[1]是比较可行的手段。利用时序建模方法对精度进行检验，有人对仿真系统和实际系统产生的数据分别进行建模，比较两模型的系数及阶数是否一致；但是由于时间序列建模是建立在平稳时间序列基础之上[2]，对于非线性和时变性的时间序列，难以检验任意状态下仿真系统的可靠性。本文提出对仿真系统输入与实际系统相同的控制参数，比较两系统的输出参数值，从而得到参数的误差序列，该误差序列经过预处理基本平稳，可以对该序列进行时间序列建模来测定仿真系统的精度。

1 时间序列分析及建模

时间序列分析的前提是建模，而进行建模之前必须对数据进行整理和检验，以得到平稳的时间序列，该工作属于预处理。预处理之后对数据序列进行建模，确定模型的阶数及参数，最后检验模型的稳定性。

1.1 预处理

主要包括对数据序列剔除野点，进行均值、方差和概率直方图分析，数据的正态性检验，独立性检验，平稳趋势的检验，提取趋势项。野点剔除方法基本思想是产生一个曲线的平滑估计[3]，然后把野点从数据中减掉。由于只能得到有限的随机变量的样本，而不是时间无限的长时记录，因此要用样本均值和样本方差来对总体参数作估计。样本概率密度或概率直方图可以帮助分析数据的分布性质，同时也有助于判断数据是否“正常”或“合理”。

在实际问题中，直接得到的数据往往带有噪声，是一种呈现较强的周期性、含有线性或缓慢变化趋势、且随机性很强的非平稳的时间序列；因此，对建模的样本数据必须进行平稳化处理，提取出趋势项[4]，以消除其非平稳周期分量，然后再按平稳随机过程进行分析建模。设原始数据序列{xi}的数学模型为xi=pi+yi，其中pi为周期项；yi为平稳随机项。分解之后，就可以对yi进行时序建模，进而对{xi}进行分析。

1.2 时间序列模型及模型检验

系统辨识就是在输入和输出数据基础上，从一组给定的模型中，确定一个与所测系统等价的模型。其中常见的时间序列模型有[5]：

（1）自回归模型 AR（p）

式中：φ1，…，φp——模型参数；

Xn——因变量；

Xn-1，Xn-2，Xn-p——“自”变量，这里“自”变量是同一变量，但属于以前各个时期的数值，所谓自回归即是此含义；

{εn，n=0，±1，…}——白噪声序列。

（2）滑动平均模型 MA（q）

式中：θ1，θ2，θq——模型参数；

εn——白噪声序列。

模型辨识条件如表1所示。

表1 时间序列模型辨识条件

本文采用波克斯-詹金斯（Box-Jenkins）方法[5]，根据样本自相关函数、偏自相关函数的统计特性，来判断误差序列适合哪一模型，进而确定其阶数和有关参数。理论上自相关函数和偏自相关函数从某个p或q值后全部截止为零，但是由于使用子样估计参数的随机性，即便是AR（p）过程，当k＞p后，系数也不会全为零，只是在零附近波动，通常还需用区间检验的方法加以判别。

模型阶次的估计采用AIC准则，而参数估计选用矩估计法。

为判断所选模型是否适当，还须通过评测与分析残差白性的方法对建模结果进行检验，其思路为[6]：对时间序列{yi}，若其模型合适，按时间序列建模的前提条件，残差序列{ni}应为一白噪声序列。残差越小，模型与实际系统的拟合程度越高。若模型不合适，则需对模型的残差作进一步分析，或重新构造模型。另外还要判断模型系统的稳定程度，也就是精度的稳定性[7]，可以通过零极点检验及分析模型的Green函数、频率特性、自协方差函数、自谱函数等特性来判断[8-9]。

2 飞行系统仿真精度的检测

2.1 建模及阶次识别

（1）用Box-Jenkins方法[10]确立模型。根据采样数据{xi}，易求得均值 μx=0.451 0，方差 σ2=2.723 3，为方便把误差序列减去均值 {xi}-μx还是记为{xi}。其样本自相关函数计算公式为

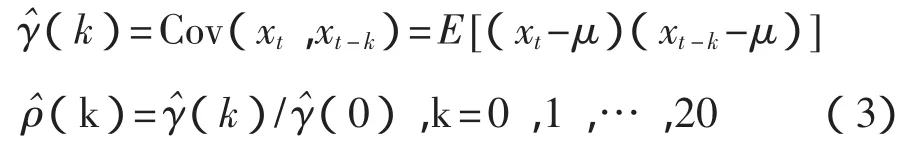
式中：k——时移，取[0，20]。

偏相关函数计算公式为

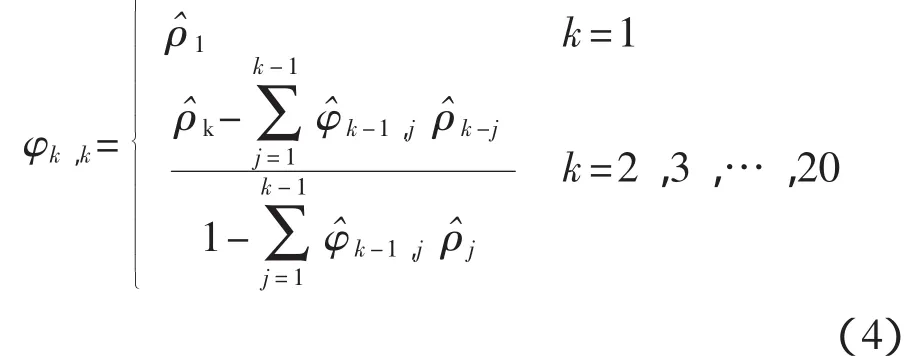
图1为自相关函数图和偏相关函数图。可以看出，自相关函数呈拖尾状，偏相关函数呈截尾状，故采用AR（p）模型。

图1 自相关函数图和偏相关函数图

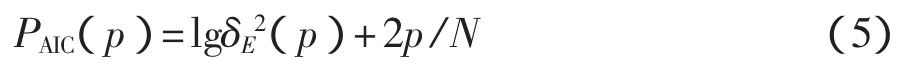
对准则函数AIC（p），真实模型的阶数p0应满足

即按函数最小的原则定阶。

采用信息量准则判断模型阶次结果表明（如图2），p=2处给出最小值，故定阶为p0=2，这里样本数据N取500。

2.2 模型参数估计

Yule-Walker方程为

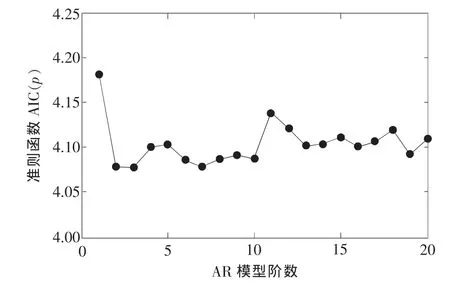
图2 误差序列的AIC值

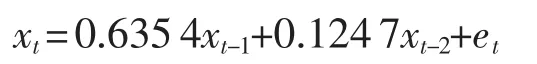
2.3 对建模结果进行检测

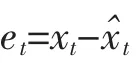
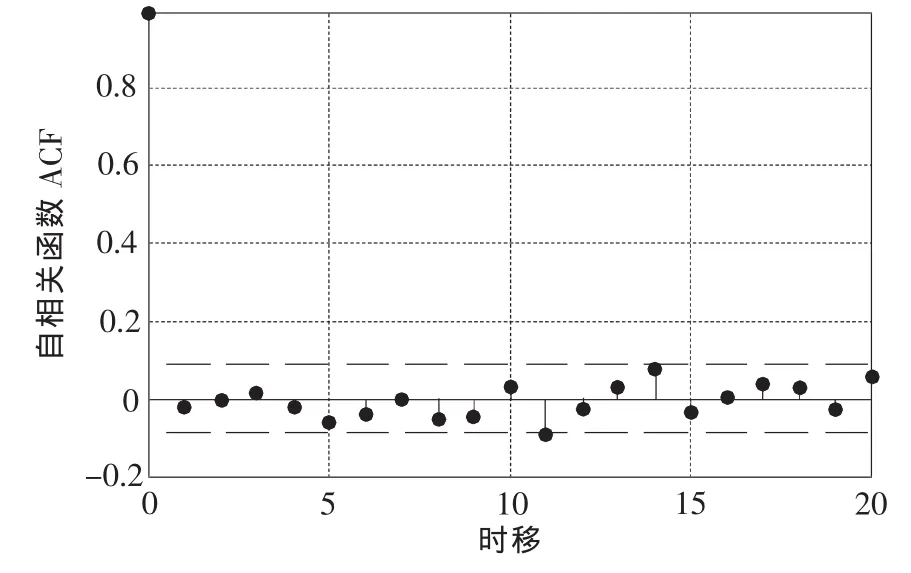
图3 残差｛et｝自相关函数

最后根据模型系统的传递函数可以获得对象的零极点，其传递函数在Z域内的零极点都分布在单位圆内，这表明系统是稳定的。只有在稳定系统中，才能保证系统精度指标满足要求。

3 结束语

本文利用时间序列建模思想来检测仿真系统精度，针对仿真系统和实际飞行系统输出的俯仰角参数误差序列进行时间序列建模，得到能够正确反映两者输出参数差别的模型，并且通过模型传递函数的零极点检验模型是否稳定，从而判断仿真系统的精度是否满足要求。实验表明，时序建模分析检测精度的方法能利用一套相当明确的准则来处理复杂的模式，直观、可行性强。但也可发现该方法计算复杂度较高。另外，该方法仅给出整个仿真系统的精度，不能确定到局部系统，若要为完善仿真体统提供更有价值的参考结果，需要做进一步的研究工作。

[1]Hamilton J D.时间序列分析[M].刘明志，译.北京：中国社会科学出版社，1999：126-132.

[2]李鹤，吕岩，李国辉.飞行仿真动态数据验证的时序建模方法[J].兵工自动化，2008，27（12）：35-37.

[3]董言治.基于时间序列模型的机载火控系统精度检测[J].电光与控制，2003（2）：32-35.

[4]芮小健，钟秉林，颜景平，等.时序建模中周期信号和趋势项的处理问题研究[J].应用科学学报，1995，2（6）：35-37.

[5]杨位钦，顾岚编.时间序列分析与动态数据建模[M].北京：北京理工大学出版社，1988：24-26.

[6]何书元.应用时间序列分析[M].北京：北京大学出版社，2007：45-48.

[7]Shuway R H，Stoffer D S.Time series analysis and its application[M].New York：Springer-Verlag，2000.

[8]吴晓明，关蓬莱.多维自回归滑动平均模型研究与应用[J].辽宁大学学报，2002，29（1）：23-24.

[9]Swami A，Mendel J M.Identifiability of the AR parameter estimatorsofan ARMA processusing cumulates[J].IEEE Trans.on Automatic Control，1992（37）：268-273.

[10]王永生，马向玲，姜文志，等.航空火控动态精度检测及数据处理分析[J].计算机仿真，2006，23（4）：37-40.