环形液池浮力－热毛细对流表面振荡现象的临界温差

张 丽，段 俐，康 琦

（中国科学院力学研究所国家微重力实验室，北京 100190）

0 引 言

浮力－热毛细对流在晶体生长和薄膜科学领域有着重要的研究价值［1－3］。过去的几十年中，浮力－热毛细对流引起了学者们的很大关注，许多理论分析、实验研究和数值模拟工作已经完成，结果证实了浮力－热毛细对流过程的转变及多种流动结构形式的存在。Schwabe等人［4－6］通过外壁加热、内壁冷却，对内外半径分别是20和40mm，深度为2.5～20mm的0.65cSt环形液池浮力－热毛细对流进行了实验研究，发现在小的水平温差下，流动为稳态的多胞流动。随着温差的增大，流动将失去稳定性，首先表现为热流体波，温差再增加时会出现更加复杂的振荡流动。石万元等人［7］利用有限容积法对外壁受热、内壁冷却、厚度为1mm的环形浅液池内硅油的热毛细对流进行了三维数值模拟。结果表明，当Marangoni（Ma）数小于临界值时，随着Ma数的增加，内、外壁附近的温度梯度上升，稳定的二维轴对称流动的径向速率增加；超过临界Ma数后，流动转化为三维振荡对流，形成热流体波，李友荣等［8］采用匹配渐进展开法研究了环形双层薄液层内的热毛细对流，得到了主流区的温度和速度分布。

由于质量守恒，对流能引起流体表面的流动形成回流［6］，因而流体表面形变与其内部流动状态有关。对中等Pr数流体（0.65cSt硅油，Pr＝6.7）的数值模拟［9］结果也表明，当水平温度梯度较小时，流动为轴对称稳态流动，随着温度梯度的增加，流动将会失去其稳定性，在浅的液池内（d＝3mm），转化成三维振荡流动，在深的液池内（d＝6mm），转化成三维稳定流动。当对流从稳定流转向振荡流时，表面就会出现振荡。本研究是基于环形液池内流体的浮力－热毛细对流实验得到的表面振荡信号来进行临界温差和环境因素分析的。

1 实 验

1.1 实验模型

实验环形液池的外径R＝20mm，内径r＝4mm，深度d＝12mm（实验时可以增加厚度垫板使液层厚度达到要求并且在位移传感器的测量范围之内）；中心为铜柱，内有电热膜，可对硅油进行加热；环壁为铜并连接半导体散热片，能将冷端维持在一个相对较低的温度；底面为绝热的K9玻璃材料。实验流体为KF96－100硅油，相关物性参数见表1。由于内外壁温差的存在，流体径向存在温度梯度，从而产生环流。环形液池模型结构可以用图1表示。

用直流电源控制高温端及散热外壁温度，使它们按照设定的温控程序变化；用热电偶实时监测中心铜柱和液池边缘的温度。实验中，两端温差逐渐升高，液层内流体的流动将从稳定态转变到不稳定态。

图1 环形液池模型Fig.1 Sketch of the experimental annuli

表1 KF96－100硅油相关物性参数（25℃）Table1 Physical parameters of the test fluid 100cSt

1.2 测量系统

为了实时测量环形液池内流体表面的振荡信息，实验采用了日本Keyence公司生产的LK－G10型号CCD激光位移传感器。它的测量原理基于三角形测量法，如图2（a）所示。反射光在CCD上的位置随着目标物位置的改变而改变，通过检测该变化就可以测量物体的位移量。在传感头的光线接收部分采用了高精度的Emostar物镜，其结构如图2（b）所示。该光学系统由4个物镜组成，其特点是像差非常小，通过其良好的成像性能，可以将不同角度的光线集中于一点，从而极大地减少了因像差所造成的光点扭曲，最大精度能达0.01μm。

图2 三角测距原理与位移传感器技术Fig.2 Triangulation ranging principle and displacement sensor technology

如图3所示，该测量系统由3部分组成：传感头、信号控制器和PC端。CCD激光位移传感器的各项参数由LK系列专用的软件LK－navigator进行设定。该软件在PC中经过USB接口将各种设定参数传送给信号控制器，再由信号控制器来决定传感头的参数。实验中，传感头以50kHz的采样频率采样，平均后得到每秒5个数据点，通过信号控制器和USB接口传送到PC终端。

图3 激光位移测量系统Fig.3 Laser displacement measurement system

1.3 典型振荡曲线

实验对环形液池中不同厚度KF96－100硅油进行了表面振荡信号的测量，分别选取液层厚度为2.5～7.5mm以0.5mm间隔递增的流体进行实验。将实验测量点固定在离铜柱中心内侧14.0mm处的一点。实验中，用温度控制器精确地控制热端的温度使它按一定速率上升，冷端基本稳定，获得水平径向温差。采用高精度CCD激光位移传感器测量获得浮力－热毛细对流自由面形变。由此得到了位移随时间变化的曲线和频谱图，如图4。

图4 位移随时间变化的曲线和频谱图Fig.4 Time－dependent displacement curve and FFT diagram

2 临界起振温差和振荡消失温差

由于理论上流体的振荡与内外温差、液池的几何尺寸及硅油本身的物理属性有关，而从图2表面振荡的信息可以推测，流体内部可能经历了一个从稳态流到振荡流，随着温差继续增大又转变为稳态流的过程。图5给出了临界起振温差ΔTc1、振荡消失温差ΔTc2与液层厚度h的关系。Lan Peng及You－Rong Li在2006年得到了外壁加热、内壁冷却时临界温差与液层厚度的关系［10］，其结果与2002年D.Schwabe的实验结果基本一致［11］。图5与上述结果的不同也说明流体振荡的临界温差还与内外加热方式有关，而流体表面振荡现象也和温度场、速度场一样成为研究流体热毛细现象及混沌转捩的一种途径。

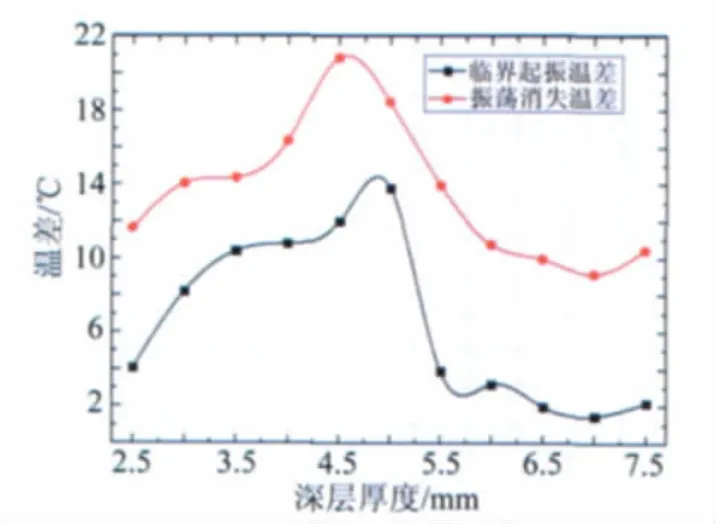
图5 临界起振温差、振荡消失温差与液层厚度的关系Fig.5 Critical appearing and disappearing temperature differences vs layer thicknesses

对于耦合了浮力对流和热毛细对流的流动，常用Rayleigh数来描述重力层流的驱动作用，用Marangoni数来描述表面热毛细作用的驱动作用，而两种作用的比可以用Bond数来描述（Bo＝Ra／Ma）。环形液池Bo数、Ma数的计算公式为：

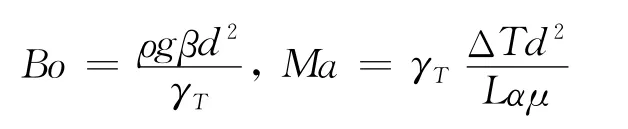
其中，β为体积膨胀系数，d为液层厚度，γT为表面张力温度系数，L为内外半径之差，α为热扩散率，μ为流体的动力粘性系数。由图5可知，在2.5～4.5mm间随着液层变厚，发生振荡的临界起振温差逐渐增大。而此时Bo数的动态范围在0.92～2.98之间，说明该区间浮力对控制对流起了主导作用。同时Ma数在此区间也是逐渐增大的（∝ΔTd2），说明热毛细对流总体也在增强。振荡临界起振温差随液层变厚而升高的现象可能是浮力和热毛细力之间存在某种不成比例的联合流场稳定控制，使流体不易失稳。而在5.5～7.0mm间Bo数继续增大，浮力对流占绝对主导，两种驱动力又形成某种联合流场失稳控制，表现为随着液层厚度增加，流场更易失稳。由此可知，虽然浮力在整个过程中是逐渐增强的，但前后表现为不同的总体控制作用，即前一阶段起稳定流场作用，后一阶段使流场更易失稳形变。这主要是因为浮力作用在流体层各处都竖直向上，与水平径向由热壁端指向冷壁端的热毛细力耦合形成热端相互增益，冷端相互抑制竞争关系的混合驱动作用；前一阶段浮力作用小，冷壁端抑制作用表现明显，后一阶段浮力作用大，热壁端增益作用冲破冷端阻碍驱动流场运动。在液层变厚的过程中，两种驱动力都在增强，但浮力的增强速度更快（Bo∝d2）。两种作用耦合竞争的“转折点”位置出现在4.5～5.5mm附近。

5.0～5.5mm之间的临界温差差值接近10℃，这是由环境温度的差异引起的。2.5～5.0mm的实验数据是在3～4月份室温较低（16℃左右）时得到的，当时温控程序初始计点温度很低（低温端设定稳定在16℃，跟环境温度接近）；而5.5mm以后的数据是在5～6月份室温较高（20℃左右）时得到的，此时温控程序初始计点温度较高（低温端设定稳定在20℃，跟环境温度接近）。室温的升高将会导致硅油膨胀，粘性减小，流体相对于低温下更容易发生形变。关于起始温度对临界起振点和消失点的影响，后文将予以讨论。

根据非线性动力学的理论，系统由稳定态向不稳定态再到混沌的转捩过程中有多种途径，目前发现的其中一种途径就是所谓的“间歇途径”，也叫“阵发性”，即系统无规则的运动和有规则运动交替出现的一种现象。在所研究的环形液池浮力－热毛细对流系统中，流动进入不稳定状态后，有规则的振荡和无规则振荡（此时多个弱信号叠加）可能交替出现。在实验温差范围内就出现了上述物理现象，即振荡短暂消失，此后是多个弱信号叠加，流体仍然是不稳定的；一旦温差再升高，强信号规则振荡仍会出现。观察首次规则振荡消失温差与液层厚度的关系曲线，发现振荡消失温差也是以4.5～5.0mm间一点为极值向两边递减，而这是相对更为可信的。因为各组实验的环境温度虽不同，但是由于振荡消失时高温端在30℃上下，低温端也已经超过20℃，所以此时外界环境温度对实验流体的影响不大。

空间项目OSCILLATORY THERMOCAPILLARY FLOW EXPERIMENT（OTFE）［12］实验测量了环形液池振荡的临界条件，提出用Ma数和表面畸变参数S来表征：

Y.KAMOTANI等［12］的结果表明：对于Pr数在26～29的2cSt，固定加热铜柱半径与液池外径之比（Rh／R）Hr＝0.1，几何深宽比（H／R）A＝1，液池径向尺寸R变化，S大于18时振荡即发生；地面临界Ma虽然大于空间，但S基本不随Ma变化而变化。

实验为地面实验，R＝20mm，Rh＝r＝4mm，Pr＝909，Hr＝0.2，0.125≤A≤0.375，得到表面畸变参数S与液池尺寸参数A的关系如图6所示。

图6 临界自由面畸变参数S与液池尺寸参数A之间的关系（Pr＝909）Fig.6 Relationship between deformation parameter Sand geometry parameter A（Pr＝909）

由图6分析出：（1）A≤0.25的情况。S与A大致呈现出线性关系，振荡区域集中出现于0.03≤S1≤0.27，0.08≤S2≤0.47所夹的｜ΔS｜≤0.2的狭长窄带区域内。在此期间，随着液层厚度的增大，发生振荡的临界畸变参数S也增大，此时在热毛细作用下液面只有发生大变形才能激发振荡，而且振荡发生后，形变幅度也是增大的。（2）0.275≤A≤0.375的情况。在A＝0.25附近，S有一个大幅度下降，此后尽管A增大，但S1仍旧在0.1附近徘徊，S2也在0.5左右小幅上升。振荡区在S1≤S≤S2的范围内存在，而且区域向上拉大，说明此处浮力对流强度的快速增长导致自由界面在大温度梯度下长时间保持不稳定，这是与A≤0.25的情况完全不同的。但是，本实验起振点处临界S值比Y.KAMOTANI等人的结果小很多，这是因为对于固定液池半径R的模型，基本为一常数3.1×10－3，这就比Y.KA－MOTANI实验中使用的2cSt这一系数低一个数量级。而且100cSt的临界Ma也比2cSt低近两个数量级，所以实验的结果是合理的。可见对于大Pr数流体，流体振荡区可能呈现的是一个喇叭状的变化趋势，这也是浮力和热毛细力耦合作用的结果。

3 起始环境温度对临界温差的影响

实验中发现，起始温度对临界起振温差、振荡消失温差有很大的影响。为了形成对照，实验设置了不同初始环境温度，相同升温速率的升温曲线见图7。

显然，图8（a）说明较低初始温度（高温端19℃，低温端17℃）时，临界起振温差普遍高于较高初始温度（高温端22℃，低温端20℃）时的情况，最高在3.5mm时相差可达0.95℃。此外，低初温时以3.6mm为极值位置两边递减，高初温时以3.9mm为分界。由于表面振荡是热毛细对流和浮力对流耦合的综合表现，起振点的变化也就说明了表面张力和重力作用耦合的“权衡点”在上述两种情况下分别出现在3.6和3.9mm处。换言之，在该种尺寸环形液池KF96－100硅油实验中，初始温度为17℃时，3.6mm以下可以认为是薄层流体，3.6mm以上则是厚层流体；初始温度为20℃时，3.9mm以上才被认为是厚层流体。同样，图8（b）也说明了初始温度17℃时振荡消失要比初始温度20℃要来得迟一些。由此可以得出结论，外界环境温度升高将会导致硅油膨胀，粘性减小，流体相对于低环境温度下更容易发生形变。

4 较强信号位置

实验还发现起始温度对振荡段主频、幅值具有影响。由于各温差下信号的主频和幅值是不同的，如果要比较各个厚度、各个温差下的主频和幅值，不仅工作量大，而且意义不大。实验中只选了振荡段来进行分析，因为区别于矩形液池的一个很大不同就是环形液池的信号有一个很明显的振荡段，而且开始点和结束点都很明显，研究振荡段的频率和幅值有助于我们了解流体本身的属性，如图9所示。

图9 两种情况下主频、主频幅值和厚度的关系Fig.9 Primary frequency and its amplitude vs layer thickness under two different conditions

由图9可见，初始温度为17℃时振荡段主频除4.5mm处外，其余均低于初始温度为20℃时的主频，可以理解为随环境温度升高，表面振荡信号“蓝移”。低温时频率以3.5mm附近为极小值向两侧递增，高温时频率以4.0mm附近为极小值向两侧递增。即，随着环境温度的升高，振荡频率和液层厚度的关系呈抛物线向前推进（本实验厚度测量范围内）。此外，由同一点不同厚度的两种情况下得到的主频幅值可知，高温下主频幅值除4.0mm处之外要低于低温下得到的幅值，这就解释了为什么低温下得到的振荡信号要比高温下明显得多。两种温度下主频幅值均在4.0mm处达到最大，这也预示着该厚度下离铜柱中心14.0mm处的该点无论环境温度高低都能得到一个较强的信号。

5 结 论

本实验开展了对环形液池浮力－热毛细对流流体表面振荡问题的研究，获得了较有意义的实验结果。无量纲分析表明，浮力随液层变厚在整个过程中逐渐增强，但前后表现为不同的控制作用，前一阶段起稳定流场作用，后一阶段使流场更易失稳形变；明显振荡段起振温差和振荡消失温差变化的转折位置也说明，表面张力和浮力作用相“权衡”时液层的大概厚度在4.5～5.5mm左右。对于大Pr数流体，振荡区SA关系图可能呈现一个喇叭状的变化趋势，这也是表面振荡是热毛细对流和浮力对流耦合的综合表现。此外，通过对照实验可知，随环境温度升高，表面振荡信号的频率出现“蓝移”；较低环境温度（17℃）下得到的振荡信号要比较高环境温度（20℃）下明显得多；且两种环境温度下主频幅值均在4.0mm处达到最大，这预示着该液层厚度下在离铜柱中心14.0mm处的该点无论环境温度高低都能得到一个较强的信号。

［1］ YANG Y K，KUO S.Temperature oscillation in a tin liquid bridge and critical Marangoni number dependency on Prandtl number［J］.Journal of Crystal Growth，2001，222：135－143.

［2］ DUAN L，KANG Q，HU W R.The characters of surface deformation and surface oscillation in buoyant－thermocapillary convection［J］.The Journal of the Japan Society of Microgravity Application，2007，24（1）：49－53.

［3］ 胡文瑞，徐硕昌.微重力流体力学［M］.北京：科学出版社，1999.

［4］ BENZ S，SCHWABE D.The three－dimensional stationary instability in dynamic thermocapillary shallow cavities［J］.Experiments in Fluids，2001，31：409－416.

［5］ SCHWABE D.Buoyant－thermocapillary and pure thermocapillary convective instabilities in Czochralski systems［J］.J.Crystal Growth，2002，237－239：1849－1853.

［6］ SCHWABE D，ZEBIB A，SIRE B C.Oscillatory thermocapillary convection in open cylindrical annuli.I.Experiments under microgravity［J］.J.Fluid Mech，2003，491：239－258.

［7］ 石万元，李友荣，彭岚，等.环形浅液池内热流体波的本质特征［J］.Chinese Journal of Computational Mechanics，2009，26（1）：59－65.

［8］ 李友荣，王双成，石万元，等.环形腔内双层薄液层热毛细对流的渐进解［J］.Chinese Journal of Theoretical and Applied Mechanics，2010，42（2）：306－311.

［9］ 彭岚，李友荣，曾丹苓，等.环形液池内中等Pr数流体的浮力一热毛细对流［J］.ACTA M ECHANICA SINICA，2005，37（3）：266－271.

［10］ PENG L，LI Y R，SHI W Y，NOBUYUKI Imaishi.Three－dimensional thermocapillary－buoyancy flow of silicone oil in a differentially heated annular pool［J］.International Journal of Heat and Mass Transfer，2007，50：872－880.

［11］ SCHWABE D.Buoyant－thermocapillary and pure thermocapillary convective instabilities in Czochralski systems［J］.Journal of Crystal Growth，2002，237－239：1849－1853.

［12］ KAMOTANI Y，OSTRACH S，PLINE A.Microgravity experiments and analysis of oscillatory thermocapillary flows in cylindrical containers［J］.J.Fluid Mech，2000，410：211－233.