利用RBF神经网络对GPS广播星历插值*

陶庭叶 高 飞 刘文星 张春喜

(1)合肥工业大学土木与水利工程学院，合肥 230009 2)武汉大学卫星导航定位技术中心，武汉 430079 3)安徽省北斗卫星导航重点实验室，合肥230088)

利用RBF神经网络对GPS广播星历插值*

陶庭叶1，2，3)高 飞1)刘文星1)张春喜1)

(1)合肥工业大学土木与水利工程学院，合肥 230009 2)武汉大学卫星导航定位技术中心，武汉 430079 3)安徽省北斗卫星导航重点实验室，合肥230088)

针对多项式插值计算任意时刻GPS卫星坐标过程中出现的Runge现象，提出了采用径向基函数(Radial Basis Function，RBF)神经网络对GPS广播星历计算所得卫星坐标进行插值。选用2011-07-25日广播星历，利用径向基函数神经网络插值计算GPS卫星坐标，并将其与直接法计算的GPS卫星坐标比较，结果表明该方法能有效避免Runge现象，提高了插值稳定性，插值精度高，可满足GPS单点定位的需求。

GPS单点定位;广播星历;径向基函数神经网络;插值;Runge现象

1 引言

利用GPS导航定位，必须计算出卫星在相应时刻的坐标，而卫星的坐标主要通过星历计算得到。GPS实时导航定位采用的广播星历可直接从GPS的导航电文中获得。在GPS定位中，常常需要多次计算卫星的位置和速度，利用广播星历计算卫星坐标时，公式繁琐，影响计算速度［1，2］，为此，常将卫星星历用一个时间多项式来表示，利用多项式拟合、插值任意时刻的卫星坐标。这里，内插的要求是不能明显损失原始星历的精度。

目前，对GPS广播星历计算得到的卫星坐标拟合与插值最常用的方法是基于Chebyshev与 Lagrange多项式的方法，这种方法一个明显的缺点是出现Runge(Runge Phenomenon，RP)现象［3］。所谓RP是指随着插值多项式阶数升高，在插值区间的两端出现振荡现象，导致两端的插值精度急剧下降。RP现象是由于节点选取的随机性和多项式基函数的绝对值之和无界，在区间端点附近易产生震荡，从而不能保证高阶插值的稳定性［4］，需要采取分段滑动拟合或减小步长等方法来减小其影响，但是，这种方法会增加计算量。

针对利用多项式对GPS广播星历的卫星坐标插值出现RP现象的问题，本文提出了利用径向基函数(Radial Basis Function，RBF)神经网络对卫星坐标进行插值，通过试验验证该方法对广播星历卫星坐标插值具有高效性、高精度与通用性的特点。

2 RBF神经网络插值与拟合原理

2.1 RBF神经网络［5，6］

RBF网络是一种三层前向网络。输入层由信号源结点组成。第二层为隐含层，隐单元数视所要描述的问题而定。第三层为输出层，它对输入模式的作用做出响应。从输入控件到隐含层空间的变换是非线性的，而从隐含层空间到输出层空间变换是线性的。

RBF网络的基本思想:用RBF作为隐单元的“基”构成隐含层空间，将输入矢量直接(即不需要通过权连接)映射到隐空间，当RBF的中心点确定后，映射关系也就确定了。隐含层空间到输出空间的映射是线性的，即网络的输出是隐单元输出的线性加权和，此处的权即为网络的可调参数。从总体上看，网络的输入到输出的映射是非线性的，而网络输出对可调参数而言又是线性的。这样网络的权就可以由线性方程组直接解出，从而大大加快了学习速度并避免了局部极小问题。

RBF网络的关键在于隐含层节点径向基函数的非线性逼近性能，一般采用的径向基函数是Gauss分布函数，即隐含层节点k的传递函数表达式为:

输出层节点相应的输出可以表示为

分两个阶段训练RBF网络，第一步是决定隐含层神经元的数量M，以及决定每个神经元的高斯函数的宽度σk和中心点Tk;第二步是使用训练数据根据全局误差准则训练权值ωk，使RBF网络拟合训练数据最佳。其中，隐含层神经元数量的确定是关键问题，传统的做法是使其与输入向量的元素相等。

RBF神经网络的学习算法为:

随机选取h个训练样本作为聚类中心ci(i=1，2，…，h)，将输入的训练样本集合按最近邻规则分组，计算各个聚类集合中训练样本的平均值，即新的聚类中心，如果新的聚类中心不再发生变化，则所得到的聚类中心即为RBF网络的聚类中心。

RBF神经网络的基函数为高斯函数，因此方差σi的解为:

式中cmax为所选取中心之间的最大距离。

应用最小二乘法对网络输出权值进行训练，其学习训练的目标是使总误差达到最小。

RBF神经网络实现的是非线性映射，理论已经证明，只要隐含层神经元数足够多，RBF神经网络可以任意精度逼近任何单值连续函数［7］。

2.2 RBF神经网络插值

采用RBF神经网络进行插值的具体算法如下:

1)将输入数据xi(i=1，2，…，N)作为样本集，将yi(i=1，2，…，N)作为输出集;

2)计算各样本的聚类中心;

4)采用RBF神经网络进行插值。

3 基于RBF神经网络GPS卫星坐标插值试验与结果分析

利用RBF神经网络拟合GPS广播星历的卫星坐标，在保证精度的前提下，避免高阶多项式拟合出现RP现象。

GPS卫星接收机所接收到的广播星历的时间间隔为2小时，即所获得的广播星历的时间是0时0分0秒、2时0分0秒直到23时45分0秒(24时0分0秒为第2天广播星历的开始时刻)。要计算某一时刻某一卫星的坐标，可根据与该时刻最接近的整点广播星历，采用直接法［1］计算出该GPS卫星在该时刻的坐标。

选取2011-07-25日广播星历，按照5秒的时间间隔计算00:20:00—00:59:00之间的PRN31卫星(任意选取)的坐标，取100个历元的数据，每5个历元抽取1个历元的卫星坐标共计20个历元的数据作为已知输入数据，用于训练神经网络，利用网络对这20个历元之间的卫星坐标进行插值。

由于RBF神经网络的径向基函数的扩展参数对插值的结果影响很大，过大或者过小的参数都不能得到好的插值结果，因此，本文采用搜索的方法确定合适的扩展参数。

利用RBF神经网络对卫星坐标进行拟合插值，将插值所得坐标与直接计算得到的坐标进行比较，得到插值残差。同理，将X坐标换成对应时刻的Y坐标与Z坐标的数据，建立相应的RBF神经网络进行拟合插值，得到的结果如图1所示。

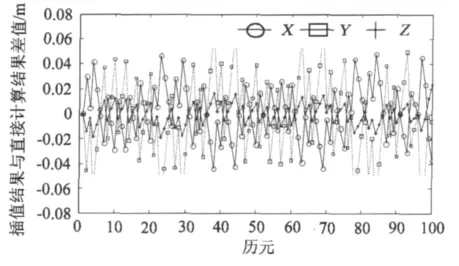
图1 PRN31卫星坐标插值残差Fig.1 Residuals of PRN31 satellite coordinate interpolation

从图1可以看出，采用RBF神经网络可以对任意时刻的卫星坐标进行插值，在节点时刻中间区域插值计算结果非常平稳，在两端也没有大幅度振荡现象。

根据广播星历，采用直接法计算其他时刻、其他卫星的坐标，利用上述方法进行插值，所得结果与2011-07-25日 00:20:00—00:59:00之间的PRN31卫星坐标插值结果类似，在此不一一列出。

这里的插值误差的大小受RBF神经网络的径向基函数扩展参数影响，选定合适的参数可以使插值的最大误差达到厘米级甚至更高，如果要进一步提高精度只需要调整径向基函数的扩展参数即可，这也验证了RBF神经网络可以任意精度逼近任何单值连续函数。

一般说来，单点定位误差的量级大体上与卫星星历误差的量级相同，而卫星坐标的基本要求就是不降低原有的卫星坐标精度，因此，插值误差在厘米级水平就能满足单点定位的要求。根据这一要求，插值过程中我们设定阈值为0.1 m，在程序中不断调整径向基函数的扩展参数，当插值误差达到厘米级精度时，停止调整并选择该参数进行坐标插值。

采用RBF神经网络对GPS广播星历坐标进行插值，针对不同的数据，要达到指定的精度，必须要选择合适的网络参数，如果参数的初始值选用不恰当，则需要花费很多的计算时间来搜索确定正确的网络参数。针对GPS广播星历卫星坐标的插值，如何确定合适的网络参数，还需要进一步研究。

4 结论

采用RBF神经网络对GPS广播星历所计算得到的GPS卫星坐标进行了拟合插值，结果表明:

1)利用RBF神经网络对GPS广播星历计算得到的卫星坐标插值残差均在厘米级别甚至更好，并且在节点时刻中间区域插值计算结果非常平稳，避免了多项式插值出现的RP现象;

2)RBF神经网络对于GPS卫星坐标插值的精度受网络的径向基函数的扩展参数影响，本文采用搜索的方法确定合适的参数，搜索的时间由参数的初始值确定，如何确定合适的网络参数初始值还有待进一步研究。

1 李征航，黄劲松.GPS测量与数据处理［M］.武汉:武汉大学出版社，2005.(Li Zhenghang and Huang Jinsong.GPS surveying and data processing［M］.Wuhan:Wuhan University Press，2005)

2 冯炜，等.两种常用GPS星历拟合方法的精度分析［J］.大地测量与地球动力学，2010，(1):145-149.(Feng Wei，et al.Accuracy assement of two fitting methods for GPS precise ephemeris［J］.Journal of Geodesy and Geodynamics，2010，(1):145-149)

3 Milan Horemuž and Johan Vium Andersson.Polynomial interpolation of GPS satellite coordinates［J］.GPS Solutions，2006，(10):67-72.

4 李庆杨，王能超，易大义.数值分析［M］.北京:清华大学出版社，2001.(Li Qingyang，Wang Nengchao and Yi Dayi.Numerical analysis［M］.Beijing:Tsinghua University Press，2001)

5 Robert H N.Theory of the back-propagation neural network［J］.Proc UCNN.，1989，(1):593-605.

6 Hint K J.Extending the functional equivalence of radial basis function network and fuzzy inference system［J］.IEEE Trans on Neural Networks，1996(3):776-781.

7 杨行峻，郑君里.人工神经网络与盲信号处理［M］.北京:清华大学出版社，2002.(Yang Xingjun and Zheng Junli.Artificial neural network and blind signal processing［M］.Beijing:Tsinghua University Press，2002)

INTERPOLATION TECHNIQUE BASED ON RBF NEURAL NETWORK OF GPS BROADCAST EPHEMERIS

Tao Tingye1，2，3)，Gao Fei1)，Liu Wenxing1)and Zhang Chunxi1)

(1)School of Civil and Hydraulic Engineering，Hefei University of Technology，Hefei 230009 2)GNSS Research Center，Wuhan University，Wuhan 430079 3)Beidou Key Laboratory of Anhui Province，Hefei 230088)

Using the RBF(Radial Basis Function)neural network to interpolate the GPS satellite coordinate computed by broadcast ephemeris was proposed in order to solve the problem of Runge Phenomenon(RP)in polynomial interpolation.The GPS satellite coordinate calculated by GPS broadcast ephemeris in 25th，July 2011 were selected to test the RBF neural network interpolation method.The interpolation results compared with the GPS satellite coordinate calculated by direct computation method show that RBF neural network interpolation method can avoid the RP，improve the interpolation stability and accuracy as well meet the demands for GPS point positioning.

GPS point positioning;broadcast ephemeris;RBF(Radial Basis Function)neural network;interpolation;Runge Phenomenon(RP)

1671-5942(2012)02-0044-03

2011-10-21

国土环境与灾害监测国家测绘局重点实验室开放基金(LEDM2010B08);合肥工业大学博士专项基金(2010HGBZ0564);合肥工业大学大学生创新性实验计划项目(cxsy102196)

陶庭叶，男，1980年生，博士，讲师，主要从事GPS高精度测量、变形监测方面的教学科研工作.E-mail:czytty@163.com

P207

A