定热流热响应实验确定岩土热物性方法

卢 军，黄光勤，徐永军

（重庆大学 三峡库区生态环境教育部重点实验室，重庆 400045）

土壤源热泵利用地下常年恒温的岩土作为低品位冷热源，通过热泵技术将浅层地热能转换为高位能源用以建筑供冷供热。近年来，中国土壤源热泵应用日益广泛，也成为研究热点，如地埋管换热器传热模型的研究[1－4]，换热器吸放热量不平衡导致地下冷／热积累问题的研究[5－6]，确定土壤热物性的热响应实验研究[7－14]等。

许多学者做了大量关于确定岩土热物性的研究[7－14]。目前，基于岩土热响应实验确定岩土热物性参数的研究最为流行，且较多大型工程中亦采用此方法确定土壤热物性设计参数，中国规范中明确提出：“当地埋管地源热泵系统的应用建筑面积在5000m2以上，或实施了岩土热响应实验的项目，应利用岩土热响应实验结果进行地埋管换热器的设计，…”。文献[7-8]研究了定地理管热流热响应实验确定岩土热物性的方法；另外，文献[8]根据无限长柱热源模型，研究了定进口温度热响应实验确定岩土热物性的方法。目前，对不同传热模型耦合不同数据处理方法对确定岩土热物性影响的研究甚少，本文通过分析用于热响应实验的各传热模型的区别，耦合不同传热模型和不同热响应实验数据处理方法，研究分析其对岩土热物性计算结果的影响，得出不同传热模型和数据处理方法对岩土热物性确定的适应性条件，提出三参数估计加权平均方法确定岩土热物性及钻孔热阻。

1 地埋管传热模型

目前，用于岩土热响应实验数据处理的地埋管传热模型主要有无限长线源模型（ILSM）及无限长柱源模型（ICSM）。ILSM用于定热流条件的热响应实验，ICSM既可用于定热流条件，也可用于定地埋管进口温度条件下的热响应实验。本文研究定热流条件下的热响应实验，在ILSM及ICSM基础上，研究了有限长线源模型（FLSM），分析了该模型是否适合用于热响应实验数据处理；最终应用不同传热模型计算岩土热物性参数。

1.1 无限长线源模型

ILSM模型将地埋管换热器假定为处于初始温度均匀、无限大介质中的无限长线热源，该模型对小管径、长时间运行的系统有较高精度，是目前大多数土壤源热泵系统设计的理论基础。换热器周围温度场分布的表达形式为：

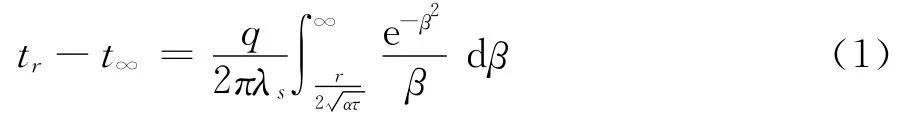
式中：τ为时间，s；r为距钻孔中心的距离，m；tr为距钻孔中心r处岩土温度，℃；t∞为岩土无穷处温度，℃；q为单位井深换热量，W／m；λs为岩土导热系数，W／（m·℃）；α为岩土热扩散率，m2／s。（1）式等价变换为热阻形式为：

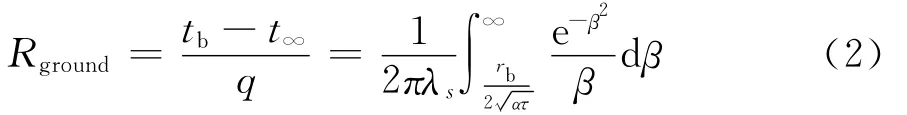
式中：Rground为钻孔壁面至无穷远处的热阻，（m·℃）／W；tb为钻孔壁温度，℃；rb为钻孔半径，其他参数同上。

1.2 无限长柱源模型

ICSM模型假定地埋管换热器处于初始温度均匀、无限大介质中，且近似为无限长圆柱热源。该模型忽略钻孔内材料的热容量，把管内流体的加热热流瞬时施加于孔壁上，也是一种对钻孔内传热过程的简化近似模型，加热时间较短时与实际情况偏离较大。钻孔周围温度场分布的表达式为：

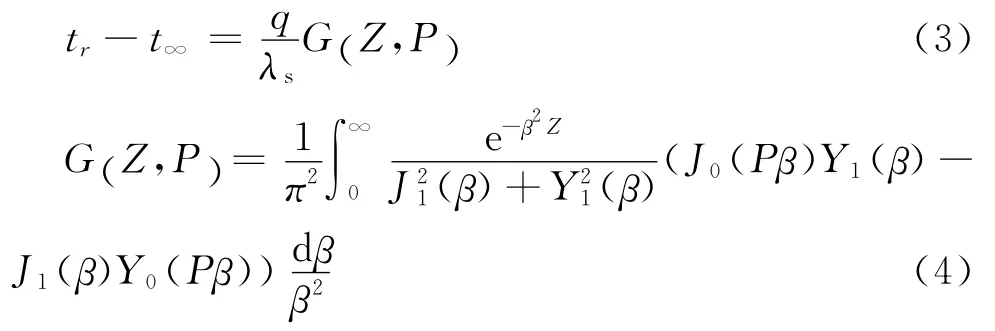
式中：J0（x）、J1（x）分别为0阶、1阶第1类贝塞尔函数；Y0（x）、Y1（x）分别为0阶、1阶第2类贝塞尔函数；其他参数同上。（3）式等价转换为热阻表达形式为：

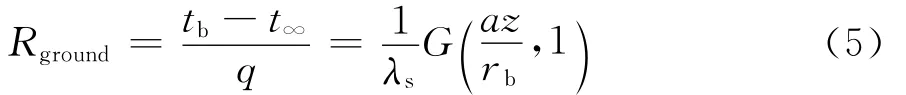
1.3 有限长线源模型

ILSM模型是对无限长线源模型改进的结果。模型考虑了岩土的有界性，将岩土假定为表面温度恒定的半无限大介质，地埋管换热器假定为有限长均匀发热的线热源，模型更能反映实际情况。埋管周围温度场分布表达式为：

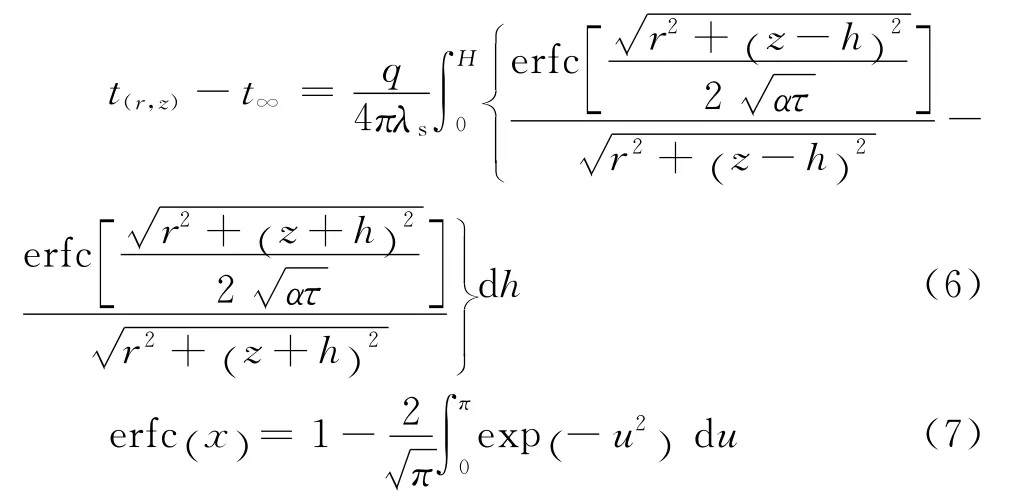
式中：H 为钻孔深度，m；z为计算点深度，m；erfc（x）为余误差函数；其他参数同上。（6）式等价转换为热阻表达形式：

1.4 模型对比分析

基于数值计算的复化Simpson求积方法，取重庆典型地质的岩土热物性λs＝2.5W／（m·℃），α＝1×10－6m2／s，分别求得ILSM、ICSM 及 FLSM 钻孔壁面至无穷远处的热阻，对比分析模型差异，在本文研究范围内，计算误差限为10－6。

1.4.1 ILSM与ICSM对比分析 ILSM与ICSM两模型最大不同在于：ILSM中地埋管换热器假定为无限长线源，而ICSM将地埋管假定为无限长柱源。计算两模型钻孔外热阻随时间变化的结果，见图1。模型计算结果表明：ILSM与ICSM在热响应初始阶段，最大相对差距达到63.6%，随时间的增加，差距逐渐减少，大约12h后相对差距小于5%；由图1可知，当时间趋与较长时，如大于15a后，两模型又开始分离，相对差距逐渐增大，对于热响应实验数据处理所用模型，出现该现象的原因可能是，时间过长，计算精度下降问题，但是针对本文研究范围，该现象对岩土热物性和钻孔热阻的确定无影响。

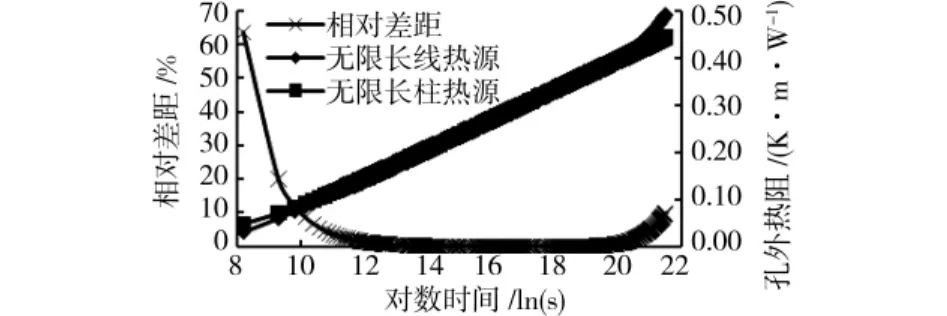
图1 无限长线热源与无限长柱热源模型的对比分析

1.4.2 ILSM与FLSM对比分析 相对ILSM模型，FLSM考虑了岩土介质及地埋管管长的有界性，更加符合实际情况。图2为两模型热阻计算结果，从图可以得出：初始响应时段内，相对差距逐渐减少；作用时间在1a以内，两模型高度吻合，相对差距小于0.1%，当作用时间大于15a后，误差逐渐增大，两模型开始分离。故对于确定岩土热物性参数的热响应实验数据，采用ILSM与FLSM两种模型没有区别，同时考虑计算速度问题，文中采用ILSM模型进行热响应实验数据处理分析。

图2 无限长线热源与有限长线热源模型的对比分析

2 热响应实验数据处理方法

目前，基于定热流密度的岩土热响应实验一般有2种数据处理方法：线性推导法及参数估计法。

2.1 线性推导法

线性推导法是基于ILSM理论模型，根据指数函数的性质，（1）式近似等价于：

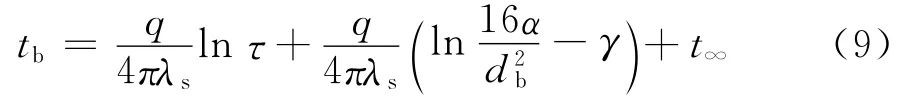
式中：db为钻孔直径，m；其他参数同上。假定钻孔内为稳态传热过程有：

式中：Rb为钻孔内热阻，（m·℃）／W，可由文献[15]求得；tf为地埋管内流体平均温度，℃；其他参数同上。结合（9）式、（10）式整理得：

由（9）式可知：tf与lnτ成线性关系，故可将热响应实验数据进行最小二乘拟合得出直线斜率k，确定岩土综合导热系数λs＝q／（4πk），根据测试得出的岩土初始温度及单位井深散热量q，结合拟合直线的截距，确定钻孔内热阻Rb。

2.2 参数估计法

参数估计法的基本思想是通过不断调整待求参数，如岩土综合导热系数、岩土热扩散率，钻孔内热阻等，当所有实验记录水温与对应时刻理论计算水温平方差求和最小时的参数值为最优计算结果。即保证目标函数f最小，f表达式为

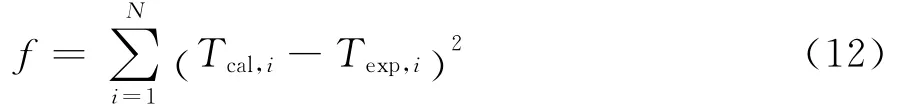
式中：f 为目标函数；Tcal，i为i 时刻理论计算水温，℃；Texp，i为i时刻实验所得水温，℃；N 为实验测量的数据组数。

该方法可以采用基于定热流边界条件的传热模型，如ILSM和ICSM等。由于钻孔内热阻当作参数估计量，无需确定钻孔内U型管布置方式。

3 结果及讨论

在重庆某2处土壤源热泵系统实际工程设计埋管区进行热响应实验，热响应实验钻孔深度均为75m，钻孔直径均为130mm。地埋管换热器采用管径为Dn25的单U型垂直埋管形式，回填材料为20%膨润土和80%SiO2的混合物。根据钻孔得到的岩土样本分析可知，工程所在地的岩土结构为泥土层——风化层——砂岩层，其中泥土层和风化层分布在地下1.5m范围内，地下岩土类型主要为砂岩。

实验采用定热流加热方法，并自主研发的一套适合定热流岩土热响应实验的实验系统，系统主要包括保温水箱、加热功率在1.5～9.5kW范围的可调节的电加热器、循环水泵、Pt－100热电偶、流量计、压力表、数据自动测量记录系统等。系统流程图见图3。

实验分为2步：1）岩土初始温度测量。为避免钻孔回填过程对土壤初始温度的影响，钻孔回填完成2～3d后，进行岩土初始温度测量。2）定加热功率下地埋管进出口水温测量。实验过程中，每隔10 s自动记录一次地埋管进出口水温。

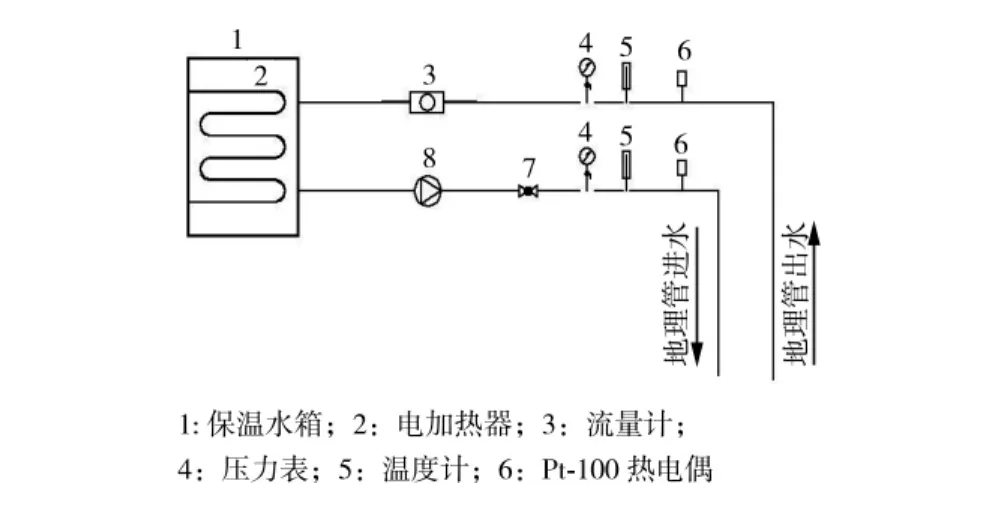
图3 热响应实验装置原理图

3.1 岩土初始温度

进行岩土热响应实验前，沿钻孔深度方向每隔5m布置温度传感器，测试岩土的初始温度。图4为初始温度竖向分布情况。由图4可知：对于孔1，深度超过15m后，温度恒定于19.84℃；随着深度增加，温度有所下降，但变化较小，温度最大波幅为0.42℃，平均温度为19.63℃。对于孔2，沿钻孔深度方向温度变化较大且逐渐升高，平均温度变化率为0.046℃／m，温度最大波幅为2.77℃，平均温度为19.25℃。造成孔2温度沿钻孔方向逐渐升高的可能原因为：孔2回填后仅保证了48h恢复时间，恢复时间不足，导致测试孔温度不能恢复至原始状态。

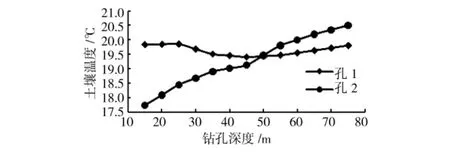
图4 沿钻孔深度方向岩土初始温度

3.2 岩土热物性

根据实测热响应实验数据，应用不同传热模型和不同数据处理方法相耦合，对比分析不同耦合方法计算的结果。采用3种不同的耦合方法：ILSM模型耦合线性推导法（ILSM-LDM）、ILSM 模型耦合参数估计法（ILSM-PE）及ICSM模型耦合参数估计法（ICSM-PE）。

3.2.1 ILSM-LDM 方法 ILSM-LDM 方法采用无限长线热源模型耦合线性推导法确定岩土热物性。该方法主要确定岩土导热系数。采用该方法确定岩土热扩散率时必须已知钻孔内U型管布置几何尺寸，而实际埋管中很难确定钻孔内实际几何参数，钻孔内稳态热阻的确定存在极大困难，故本文建议不宜采用该方法确测试孔钻孔热阻及岩土热扩散率。为了避免初始热响应阶段钻孔内非稳态导热对计算结果的影响，舍掉10h前实验数据。图5给出了取不同测试时间段对应导热系数。可以看出：对于孔1，随着测试时间的增加，导热系数逐渐变小；对测试水温进行分析发现，当测试时间30h时，由于电压波动等原因，导致水温突然降低，此时导热系数出现波峰；测试时间40h后，导热系数趋于稳定，稳定值为2.97W／（m·℃）左右。对于孔2，随着测试时间的增加，导热系数逐渐变小，无异常规律，当测试时间35h后，趋于稳定，稳定值为2.90W／（m·℃）左右。由上述可以推测：如孔1在测试时间30h左右不出现电压波动，其稳定时间将缩短。

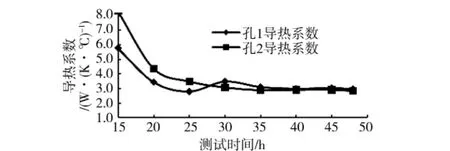
图5 ILSM-LDM方法确定的岩土导热系数变化趋势

3.2.2 ILSM-PE方法 采用ILSM-PE方法时，利用Simpson求积公式求解无线长线热源模型，相对ILSM-LDM方法中采用的指数函数近似表达式具有更高的精度。该方法将钻孔热阻当作被估计参数，无需确定钻孔内U型管的几何尺寸，估计得到的钻孔热阻具有较高可信度。计算时，分别取容积比热 ρcp＝2000kJ／（m3· K）、ρcp＝3000 kJ／（m3·K）、ρcp＝4000kJ／（m3·K）。图6及图7给出了孔1将导热系数和钻孔热阻作为被估计参数的双参数估计结果。孔2双参数估计计算结果与孔1规律相似，未列于文中。

对于孔1，由导热系数计算结果可知：导热系数随着测试时间增加的变化规律与ILSM-LDM方法所得变化规律相同，测试时间约36h后趋于稳定，较ILSM-LDM方法的计算稳定时间减少4h左右，若测试时间30h时电压不出现波动，由图6可知，测试时间24h左右后计算结果就趋于稳定了；对于不同的容积比热，导热系数变化规律一致且不同容积比热在相同时刻导热系数计算结果变化很小，最终导热系数趋于2.95W／（m·℃）。由钻孔热阻计算结果可知：稳定时间的变化规律与导热系数变化规律一致；但是对于不同容积比热，钻孔热阻稳定值相差甚大，最大相对差距达到20%，故利用双参数估计的ILSM-PE方法求解钻孔热阻不是最佳方法。

对于孔2，在测试时间12～18h期间，导热系数有较大波动，其后逐渐减小并在测试时间约35h后趋于稳定；不同容积比热对导热系数的影响很小，稳定值为2.73W／（m·℃），与ILSM-LDM 方法相比，相对差距为约6%。钻孔热阻计算结果可知，钻孔热阻随测试时间波动较大，无明显稳定趋势，不同容积比热计算得出的钻孔热阻差距较大，最大相对差距为18.2%。

图6 ILSM-PE方法确定的岩土导热系数变化趋势

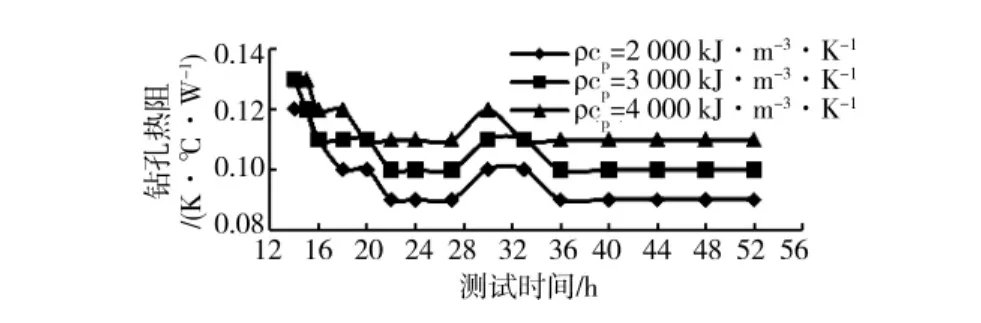
图7 ILSM-PE方法确定的钻孔热阻变化趋势

综合孔1及孔2计算结果可知，容积比热对导热系数影响很小，但是对钻孔热阻影响较大，故双参数的ILSM-PE方法对导热系数的确定有较高可信度，对钻孔热阻的求解可信度不高。

3.2.3 ICSM-PE方法 为了讨论不同传热模型对岩土热物性计算结果的影响，采用基于无线长柱热源模型的ICSM-PE方法确定热物性参数。计算无限长柱热源模型时同样采用了高精度的复化Simpson公式。与ILSM-PE方法相同，分别取容积比热ρcp＝2000kJ／（m3·K）、ρcp＝3000kJ／（m3·K）、ρcp＝4000kJ／（m3·K）进行计算。图8及图9给出了孔1将导热系数和钻孔热阻作为被估计参数的双参数估计结果。孔2双参数估计计算结果未列于文中。

对于孔1，导热系数随测试时间的变化规律同ILSM-PE方法所得规律，稳定时间也相似；不同容积比 热 下，ρcp＝2000kJ／（m3·K）与 ρcp＝3000kJ／（m3·K）及ρcp＝4000kJ／（m3·K）存在一定分离，当ρcp＝2000kJ／（m3·K）时，求得导热系数稍大于另2种容积比热情况，相对差距约12%，平均稳定值为2.70W／（K·℃），与ILSM-PE方法得到的导热系数相比，相对差距为8.8%。钻孔热阻随测试时间变化规律较ILSM-PE方法相同，不同容积比热下差距较大，最大相对差距约10%。

对于孔2，导热系数变化规律同ILSM-PE方法所得规律，稳定值为2.53W／（m·℃），与ILSM-PE方法确定的导热系数相对差距为7.6%。不同容积比热下钻孔热阻相差较大，最大相对差距20%。

同理，综合孔1及孔2计算结果可知，容积比热对导热系数影响很小，但是对钻孔热阻影响较大，故双参数的ICSM-PE方法对导热系数的确定有较高可信度，对钻孔热阻的求解可信度不高。

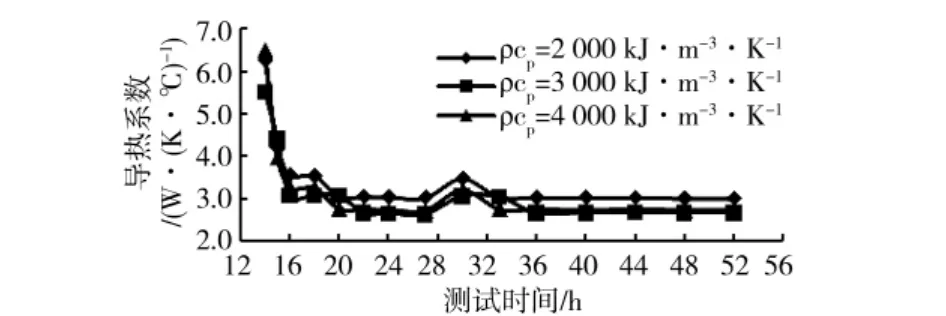
图8 ICSM-PE方法确定的岩土导热系数变化趋势

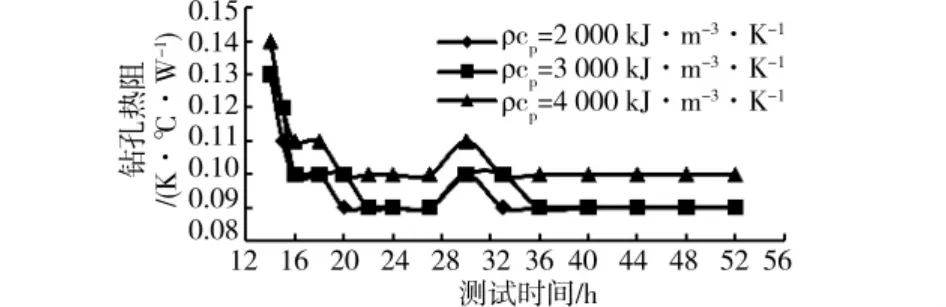
图9 ICSM-PE方法确定的钻孔热阻变化趋势

3.2.4 三参数估计方法的讨论

分析可知，利用直线推导法和双参数估计方法无法正确合理确定热扩散率及钻孔热阻。为了解热扩散率对设计容量的影响，基于文中介绍的无限长线热源模型，结合北美常用地埋管设计模型，开发了地埋管换热器设计软件。经过计算得知，当热扩散率在0.8m2／s至1.2m2／s变化时，地埋管设计容量变化5%～7%。可见工程设计中，岩土热扩散率对地埋管换热器容量的影响不可忽略。故为了合理确定热扩散率及钻孔热阻，本文采用三参数估计方法估计法，将导热系数、热扩散率及钻孔热阻当作被估计参数，采用柱热源模型和线热源模型分别确定热物性及钻孔热阻。根据两模型计算结果相对实验数据的误差，采用对2模型计算结果进行加权平均的方法确定岩土热物性及钻孔热阻。

图10—12给出了孔1三参数估计计算结果，由图10可以看出，导热系数变化规律同双参数估计；导热系数计算结果表明，线热源模型明显大于柱热源模型，稳定值相对差距为10.4%。由图11可知，基于线热源模型确定的钻孔热阻波动较大，但是最终趋于稳定；柱热源模型确定的钻孔热阻稳定性更好，2模型确定的钻孔热阻稳定值相同，其大小为0.10（m·℃）／W，说明三参数估计方法对钻孔热阻的确定可信度高。图12描述了热扩散率计算结果，可以看出，采用线热源和柱热源模型确定的热扩散率在较长测试时间内比较发散，当测试时间达到48h后，基于单一线热源模型与单一柱热源模型所确定的岩土热扩散率分别稳定于0.6×10－6m2／s，1.0×10－6m2／s，两者相对差距达到50%。由于孔1在测试时间约30h时，电压出现较大波动，导致热扩散率在测试时间约30h时波动极大。根据热扩散率总体变化趋势可推测：如无电压波动导致水温的大幅波动，热扩散率测试稳定时间将缩短。

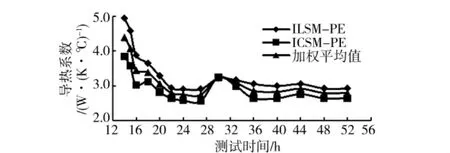
图10 三参数估计方法确定的岩土导热系数变化趋势

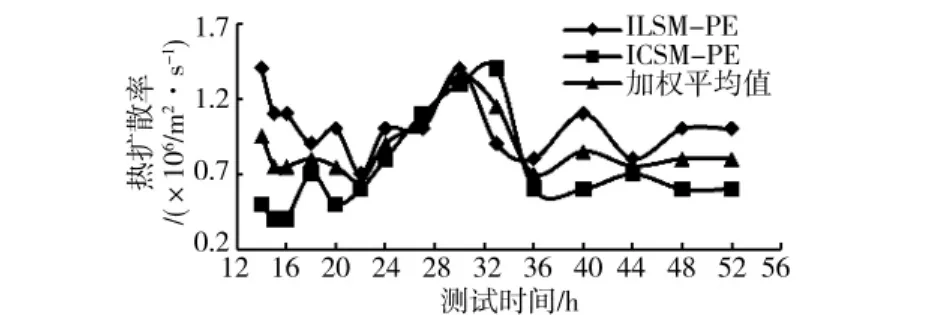
图11 三参数估计方法确定的热扩散率变化趋势

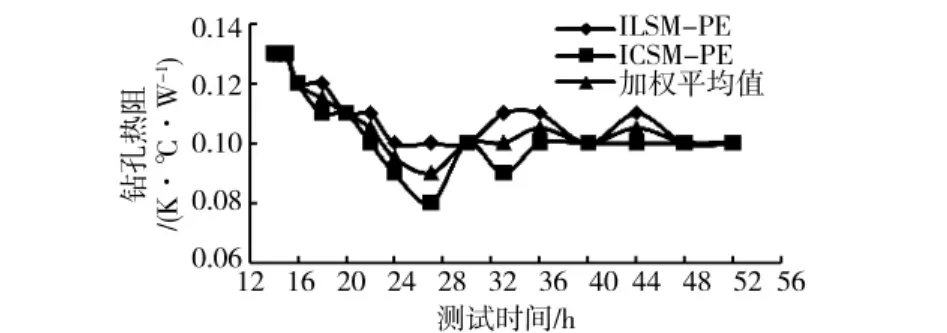
图12 三参数估计方法确定的钻孔热阻变化趋势

在适当的测试时间下，通过三参数估计方法确定的导热系数、钻孔热阻及热扩散率均能稳定，但是采用不同模型对结果影响较大，为了最终确定导热系数、钻孔热阻及热扩散率，本文采用2种模型的加权平均值作为计算结果。采用三参数估计方法时，记录了不同模型、不同测试时间下对应的最小平均误差δ，表达式为：

式中：δ为最小平均误差，℃；fmin为最小目标函数值；N为实验测量的数据组数。采用WL及WC分别作为线热源模型和柱热源模型的权值，其表达式分别为：

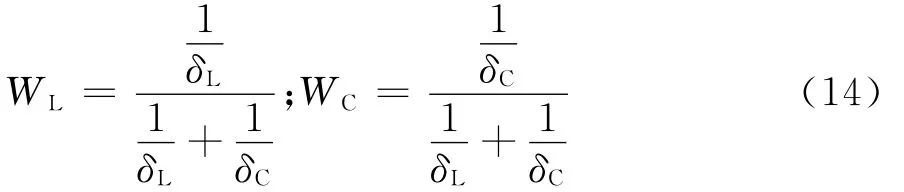
式中：WL为线热源参数权值；WC为柱热源参数权值；δL为线热源最小平均误差；δC为柱热源最小平均误差；导热系数、热扩散率及钻孔热阻加权平均值计算结果分别见图10—12，由图可以看出：加权平均钻孔热阻及热扩散率的稳定性更好，可信度更高。

理论上分析，由于线热源模型将钻孔及埋管假定为均匀恒定热流的线热源，从作用时间开始时钻孔中心就维持一恒定热流，而柱热源模型假定从作用时间开始时，圆柱面上维持一恒定热流，与实际情况相比，两模型在传热上分别存在延迟和超前效应，故采用基于平均误差分析的二者加权平均方法确定热物性及钻孔热阻具明显理论意义。

4 结 语

通过对不同传热模型耦合不同数据处理方法确定岩土热物性及钻孔热阻的研究表明：

1）采用线热源模型与柱热源模型确定的岩土热物性及钻孔热阻存在较大差异，导热系数相对差距在8.8%到10.4%。

2）采用双参数估计时，岩土容积比热对导热系数影响很小，但对钻孔热阻影响较大，双参数估计不宜用以确定钻孔热阻及热扩散率。

3）三参数估计确定导热系数及钻孔热阻具有良好可信度，但是对于热扩散率的确定稳定性较差。

4）结合三参数估计的加权平均方法，将最小平均误差作为线热源与柱热源模型权值分析的基础，确定岩土热物性及钻孔热阻具有稳定性好，可信度高的特点。

[1]赵军，张春雷，李新国，等.U型管埋地换热器三维传热模型及实验对比分析 [J].太阳能学报，2006，27（1）：63-66.ZHAO JUN，ZHANG CHUN-LEI，LI XIN-GUO，et al.Three-dimensional heat transfer model and experimental analysis of U-pipe heat exchanger [J].Acta Energiae Solaris Sinica，2006，27（1）：63-66.

[2]MAN Y，YANG H X，DIAO N，et al.A new model and analytical solutions for borehole and pile ground heat exchangers[J].International Journal of Heat and Mass Transfer，2010，53：2593-2601.

[3]曾和义，刁乃仁，方肇洪，等.地源热泵竖直埋管的有限长线热源模型 [J].热能动力工程，2003，18（2）：165-169.ZENG HE-YI，DIAO NAI-REN，FANG ZAO-HONG，et al.A model of finite-length linear heat-source for the vertical embedded pipe of a ground-source heat pump[J].Journal of Engineering for Thermal Energy and Power，2003，18（2）：165-169.

[4]黄俊惠，时晓燕，唐志伟，等.地源热泵U型管地下换热器的准三维模型 [J].中国农业大学学报，2004，9（5）：51-54.HUANG JUN-HUI，SHI XIAO-YAN，TANG ZHIWEI，et al.Pseudo 3Dmodel of ground heat exchanger for GSHP[J]. Journal of China Agricultural University，2004，9（5）：51-54.

[5]MAN Y，YANG H X，FANG Z H.Study on hybrid ground-coupled heat pump systems [J].Energy and Buildings，2008，40：2028-2036.

[6]JEON J，LEE S，HONG D，et al.Performance evaluation and modeling of a hybrid cooling system combining a screw water chiller with a ground source heat pump in a building[J].Energy，2010，35：2006-2012.

[7]于明志，彭晓峰，方肇洪，等.基于线热源模型的地下岩土热物性测试方法 [J].太阳能学报，2006，27（3）：279-283.YU MING-ZHI，PENG XIAO-FENG，FANG ZHAOHONG，et al.Line source method for measuring thermal proerties of deep ground [J].Acta Energiae Solaris Sinica，2006，27（3）：279-283.

[8]赵 军，段征强，宋著坤，等.基于圆柱热源模型的现场测量地下岩土热物性方法 [J].太阳能学报，2006，27（9）：934-936.ZHAO JUN，DUAN ZHENG-QIANG，SONG ZHUKUN，et al. A method for in situ determining underground thermal properties based on the cylindrical heat source model[J].Acta Energiae Solaris Sinica，2006，27（9）：934-936.

[9]WANG H J，QI C Y，DU H P，et al.Improved method and case study of thermal response test for borehole heat exchangers of ground source heat pump system[J].Renewable Energy，2010，35：727-733.

[10]FUJII H，OKUBO H，NISHI K，et al.An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermometers[J].Geothermics，2009，38：399-406.

[11]BOZZOLI F，PAGLIARINI G，RAINIERI S，et al.Estimation of soil and grout thermal properties through a TSPEP（two-step parameter estimation procedure）applied to TRT （thermal response test）data[J].Energy，2011，36：839-846.

[12]HWANG S，OOKA R，NAM Y J.Evaluation of estimation method of ground properties for the ground source heat pump system[J]. Renewable Energy，2010，35：2123-2130.

[13]RAYMOND J，THERRIEN R，GOSSELIN L，et al.Numerical analysis of thermal response tests with a groundwater flow and heat transfer model[J].Renewable Energy，2011，36：315-324.

[14]WANG H J，QI C Y，DU H P，et al.Improved method and case study of thermal response test for borehole heat exchangers of ground source heat pump system[J].Renewable Energy，2010：35：727-733.

[15]曾和义，刁乃仁，方肇洪，等.竖直埋管地热换热器钻孔内的热阻 [J].煤气与热力，2003，23（3）：134-13.ZENG HE-YI，DIAO NAI-REN，FANG ZAO-HONG，et al.Thermal resistance inside bore-holes of vertical geothermal heat exchangers[J].Gas ＆ Heat，2003，23（3）：134-138.