临城县西台峪板岩矿区平面控制测量的基线解算与GPS网平差初探

付佳琪

（石家庄经济学院土地资源与城乡规划学院，河北 石家庄 050031）

临城县地处太行山中段东麓，西部山区蕴藏着丰富的饰面用板岩矿资源，目前这种板岩矿经加工后用于装饰高级宾馆及公共设施墙壁，具有返璞归真，回归大自然的效果，深受人们的喜爱。为更好地利用这一资源，大规模开发当地的饰面用板岩资源，为当地群众增加就业机会和经济收入，为当地政府的规划开发提供依据，受探矿权人委托对临城县西台峪一带的饰面用板岩矿进行地质普查工作，需测绘该区域的地形图，本文对在平面控制测量中的基线解算与GPS平差的经验进行初步探讨。

1 平面控制网的布设

在测量范围内根据工程需要共新布设12个四等GPS控制点，控制点的编号为TY1-TY6、LC1-LC6，并在实地明显地物(如房角、电杆)上用红色油漆进行了标注，便于查找。所有GPS控制点都选在交通便利、视野开阔、不影响耕种和易长期保存及方便施工放样的位置。平面控制布设四等GPS网见右图。

GPS网的观测：四等GPS网共观测15个点，其中起算点3个(1170、A017、C167)，外业观测采用6台仪器同步按观测要求进行。

2 基线解算

基线解算采用徕卡测量系统有限公司研制开发的LGO6.0软件进行[2]。

2.1 基线解算精度

基线解算精度统计见表1。从表中可以看出，全部集中在0.1～1.9mm之间，精度较高[3]。

表1 基线解算精度统计(mm)

由上表可见，GPS基线的解算质量较好，为下一步的计算提供了良好的数据基础。

2.2 基线重复性检验

四等网共有重复基线6条，按《工程测量规范》中四等网精度指标要求，取：固定误差a=10mm，比例误差系数b=5，d为实际边长，代入公式σ=

统计数据表明，重复基线的位置差最大为7.3949mm，限差为319.6155mm，满足规范要求。

2.3 环闭合差检验

基线解算完后，数据预处理部分进行了环闭合差检验。

弦长精度按下式计算：

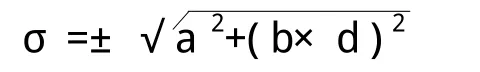
式中：σ——弦长标准差(mm)；

a——固定误差(mm)，四等网a=10mm；

b——比例误差(mm)，四等网b=5mm；

d——相邻点间的距离(km)。

异步环的坐标分量闭合差和全长闭合差应符合下式的规定：

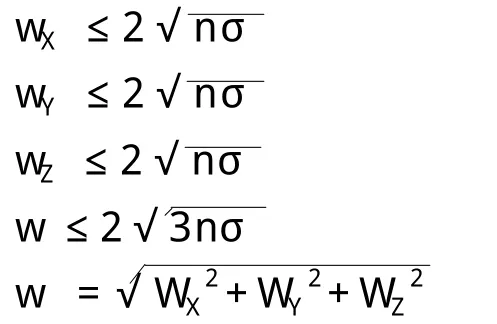
式中：w——环闭合差；

n——独立环中的边数。

共检验异步环17个，坐标分量闭合差最大为32.6mm，限差为552.48mm; 全长闭合差最大为42.83mm，限差为887.07mm，均满足限差要求。

三边同步环的坐标分量闭合差和全长闭合差应符合下式的规定：

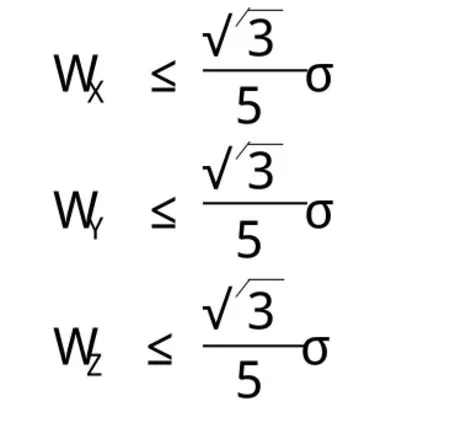
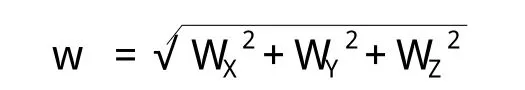
式中：w——环闭合差；

n——独立环中的边数。

共检验异步环29个，坐标分量闭合差最大为37.1mm，限差为51.1mm; 全长闭合差最大为54.2mm，限差为88.5mm，均满足限差要求。

3 GPS网平差

平面控制网平差软件：科傻GPS处理系统5.2版[2]。

GPS控制网共布设12个四等GPS控制点，联测C级GPS控制点2个(A017、C167),B级GPS控制点1个(1170)。

3.1 2000坐标系下三维无约束平差

三维无约束平差的目的主要是进行粗差分析，以发现观测量中的粗差并消除其影响，其结果客观反映了整个GPS网的内部符合精度。以1170作为起算点，进行2000坐标系下的三维无约束平差，以检测网的内附精度，获得各条基线的三维基线向量改正数以及基线边长和边长的精度信息。

三维基线向量改正数均满足下式：

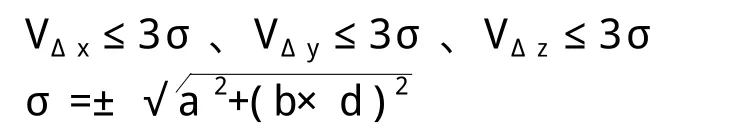
式中：σ——弦长标准差(mm)；

a——固定误差(mm)，四等网a=10mm；

b——比例误差(mm)，四等网b=5mm；

d——相邻点间的距离(km)。

平差后精度信息如下：

(1)点位中误差最大的点：LC5；

(2)Mp=1.19cm(Mx=0.49cm,My=0.82cm,Mz=0.65cm)；

(3)边长相对中误差最大的边: TY1-TY2(1/476000)。

3.2 2000坐标系下三维约束平差

以C167、A017、1170作为起算点，进行2000国家大地坐标系下的三维约束平差，以获得2000国家大地坐标系下各点的三维坐标、三维基线向量改正数以及基线边长和边长的精度信息。

约束平差后，基线向量的改正数与无约束平差结果中的同名基线相应的改正数的较差dVΔx、dVΔy、dVΔz均满足下式要求：

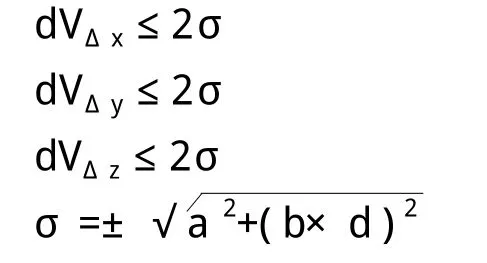
式中：σ——弦长标准差(mm)；

a——固定误差(mm)，四等网a=10mm；

b——比例误差(mm)，四等网b=5mm；

d——相邻点间的距离(km)。

平差后精度信息如下：

(1)点位中误差最大的点：LC5；

(2)Mp=3.35cm(Mx=1.43 m,My=2.35cm,Mz=1.90cm)；

(3)边长相对中误差最大的边: TY1-TY2(1/117000)。

3.3 1980西安坐标系下二维约束平差

本控制网共联测了3个高等级已知点，为检验已知点精度情况，进行了1980西安坐标系下固定2个点的二维约束平差，即以1170、C 167作为起算点，进行1980西安坐标系下的二维无约束平差，以A017为检测点。

平差后精度信息如下：

(1)点位中误差最大的点：LC5；

(2)Mp=0.31cm(Mx=0.22cm,My=0.22cm)；

(3)边长相对中误差最大的边：TY1-TY2(1/619000)。

平差结果与理论坐标比较见表2。

由以上结果可知，A 017相对于1170、C 167两点的边长相对中误差分别为1/1410130、1/804123。

表2 平差坐标与理论坐标对比(m)

可见A 017、1170、C 167可作为四等GPS控制网1980西安坐标系下二维约束平差计算的起算数据。

3.4 1980西安坐标系下二维约束平差

以A 017、1170、C 167作为起算点，进行1980西安坐标系下二维约束平差，以获得各控制点的1980西安坐标系坐标。平差结果为：参考椭球面的1980西安坐标系坐标，中央子午线为L＝114°00′00″。

平差后精度信息如下：

(1)点位中误差最大的点：LC5；

(2)Mp=0.62cm(Mx=0.44cm,My=0.43cm)；

(3)边长相对中误差最大的边：TY1-TY2(1/309000)。

4 结语

由于工程项目及科研实践的需要，对GPS数据精度的要求越来越高,如何对GPS控制网进行平差处理是能否提高精度的关键，GPS基线的解算和GPS网平差是一个复杂的平差计算过程，其精度影响到所测成果的质量，因此在今后的工作中必须引起足够的重视。

[1]袁本银,高成发.GPS基线解算与网平差的软件设计与实现[J].测绘,2009(1):1-4.

[2]郝天懿,罗新宇,胡云华.GPS基线向量网平差方法研究及程序计算[J].低温建筑技术,2012(1):53-54.

[3]付佳琪.RTK技术在临城某测区的应用及精度探讨[J].中国非金属矿工业导刊,2012(S 1):54-55.