测长仪示值误差的测量不确定度评定

董广荣

（徐州市计量检定测试中心 江苏 徐州 221002）

0 概述

1）测量方法：依据JJF1189-2008《测长仪校准规范》

2）环境条件：温度（20±1）℃

3）测量标准：三等标准量块，扩展不确定度U=0.15μm，包含因子k=2.7

4）测量对象:测长仪，测量范围（0～1000）mm，最大允许误差：1.5μm

5）测量过程

校准测长仪示值误差时，移动测量轴，使两球面测帽接触，并将测帽调整至正确状态，转动尾管的微动螺丝，使毫米刻度尺的零线与读数装置的零位对准。然后将间隔10mm的量块，依次地安装在工作台上。升降和移动工作台，使量块处于测量轴上。移动测量轴，使球面测帽与量块工作面接触。使工作台按其水平轴和垂直轴转动，找到最小值时，在仪器上读数，取各读数与所用量块的实际长度之差，即为各校准点相对零信的误差。

6）评定结果的使用

符合上述条件下的测量结果，一般可直接使用本不确定度的评定结果。

1 数学模型

△=(Li-L0)-LS

式中：△——各点的示值误差；

Li——各校准点上仪器的读数值；

L0——起始点上的仪器的读数长度；

LS——所用标准量块的实际长度。

2 输入量的标准不确定度评定

2.1 输入量Li标准不确定度u（Li）的评定

输入量Li标准不确定度来源主要是测长仪的测量重复性，可以通过连续测量得到测量列，采用A类方法进行评定。

对一台测长仪，选择10mm点，连续测量10次，得到测量列10.001、10.0000、10.0000、10.0001、10.0000、10.0000、10.0000、10.0000、10.0002、10.0002mm。

任意选取3台同类型测长仪，每台分别选3处测量点，各在重复性条件下连续测量10次，共得到9组测量列，每组测量列分别按上述计算得到单次实验标准差，如表1所示。

表1 m组实验标准差计算结果

则可得到u(Li)=Sp=0.08μm

2.2 输入量L0的标准不确定度u(L0)的评定

按3.1方法，可得到u(L0)=Sp=0.08μm

2.3 输入量LS的标准不确定度u（Ls）的评定

输入量LS的标准不确定度来源主要是标准量块的定值不确定度引起的标准不确定度分项u(Ls1)；由于测长仪和标准量块的温度线膨胀系数不同，当温度偏离标准温度20℃时引起的标准不确定度分项u(Ls2)；由于测长仪与标准量块的温度线膨胀系数的不确定度，当温度偏离标准温度20℃时引起的标准不确定度分项u(Ls3)；以及由于测长仪与标准量块温度差引起的标准不确定度分项u(Ls4)，以上可采用B类方法进行评定。

1）标准量块的定值不确定度引起的标准不确定度u(Ls1)的评定

标准量块的校准证书给出定值的扩展不确定度：U=0.15μm，包含因子k=2.7，标准不确定度u(Ls1)为：

2）测长仪和标准量块的温度线膨胀系数不同，当温度偏离标准温度20℃时引起的标准不确定度u(Ls2)的评定

校准时，温度在（20±1）℃的范围内服从均匀分布，该均匀分布的半宽α=1℃，包含因子，测长仪与标准量块温度线膨胀系数分别为（10.2±0.5）×10-6℃-1和（11.5±1）×10-6℃-1，则△α=1.3×10-6℃-1，标准不确定度u(Ls2)为：

3）由于测长仪与标准量块的温度线膨胀系数的不确定度，当温度偏离标准温度20℃时引起的标准不确定度u(Ls3)的评定

测长仪与标准量块的温度膨胀系数分别在（10.2±0.5）×10-6℃-1和（11.5±1）×10-6℃-1的范围内服从均匀分布，则△α=1.3×10-6℃-1的范围内服从梯形分布，该梯形分布的半宽α=1.5×10-6℃-1，包含因子k=，当温度偏离量△t=1℃时，标准不确定度u(Ls3)为：

4）测长仪与标准量块温度之差引起的标准不确定度u(Ls4)的评定经等温后，测长仪与标准量块温度之差估计在±0.3℃范围内服从均匀分布，该均匀分布半宽α=0.3℃，包含因子，标准不确定度u(Ls4)为：

3 合成标准不确定度的评定

表2 标准不确定度汇总表

3.1 灵敏系数

3.2 标准不确定度汇总表

输入量的标准不确定度汇总于表2。

3.3 合成标准不确定度的计算

输入量Li、L0及LS彼此不相关，所以合成标准不确定度可按下式得到：

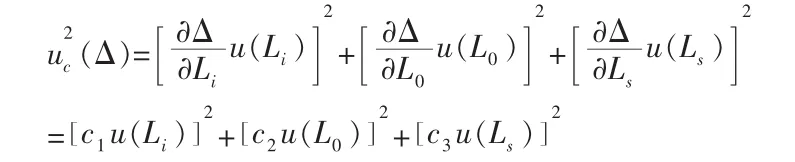
4 扩展不确定度的评定

取置信概率k=2 得到扩展不确定度为

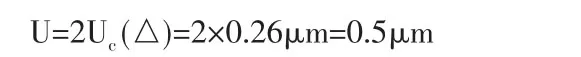
5 测量不确定度的报告与表示

测长仪示值误差测量结果的扩展不确定度为U=0.5μm