轧辊参数对铝合金薄板冷轧过程应力应变的影响

李智军，王少鹏

(西安航天动力研究所，陕西 西安 710100)

0 引言

薄板材冷轧过程中，材料厚度方向发生不均匀塑性变形，成形后板材形成鼓形截面，厚度不均匀，中间厚度大于边缘厚度，不能达到检验标准。为了保证轧制后板材厚度均匀，通常对辊型进行补偿设计，使得回弹后的轧制板材满足厚度均匀性。然而，轧辊辊型的补偿设计引起轧辊半径变化，加上轧制过程中轧辊速度存在波动，使得成形后板材厚度出现一定大小的波动，伸长应变分布不均匀，影响成形精度。因此研究轧辊参数 (包括轧辊半径和轧辊转速)对板材应力应变的影响对于确定轧辊参数合理波动范围、实现冷轧精确成形及预测具有重要意义。

最早对轧制过程的轧辊参数和应力应变研究主要基于理论解析法，如Karman微分方程，采利科夫应力和材料宽向流动理论计算公式，Freshwa-ter的轧制应力理论计算模型等［1］。随着计算机技术的飞速发展，采用有限元法对轧制过程进行分析计算已经成为精确控制研究的重要手段和发展趋势［2］。东北大学刘相华、王国栋等［3］建立了轧制过程有限元模型，对轧制变形区内材料流动行为进行分析、对轧制应力进行了预测，基于该模型可实现轧辊参数对应力应变影响的研究;丁文华等［4］建立了多道次热轧二维有限元模型，研究了轧制速度对局部特征点处等效应力和等效应变的影响。Duan和Sheppard［5］基于有限元对热轧过程接触变形区应力和厚度分布进行了研究。上述研究主要集中在轧制应力研究，对应变也仅限于等效塑性应变，缺乏对整个变形区内材料应变包括厚向应变、伸长应变和宽向应变分布的全面研究。尤其是轧辊参数对应变分布的影响规律。

为此，本文基于ABAQUS/Explicit平台建立了薄板材冷轧过程三维弹塑性有限元模型，研究轧辊参数对轧制过程应力应变分布的影响，旨在为确定轧辊参数合理波动范围、实现冷轧精确成形及预测提供借鉴。

1 有限元模型的建立

基于ABAQUS/Explicit平台，建立了铝合金冷轧过程三维弹塑性有限元模型，如图1所示。由于轧制过程轧辊对称分布，轧板沿中心对称，建模过程采用1/2对称模型。模拟过程不考虑轧辊的弹性变形，将轧辊设置为解析刚体;将板材设置为变形体，采用三维六面体缩减积分单元C3D8R划分，厚度方向上网格单元划分至少3个。摩擦系数采用摩擦扭转试验获得，在航空润滑油下，试验测得摩擦系数平均值为0.04。模拟中摩擦边界条件采用库伦摩擦模型［6］。为了提高计算效率，取质量放大因子为400。

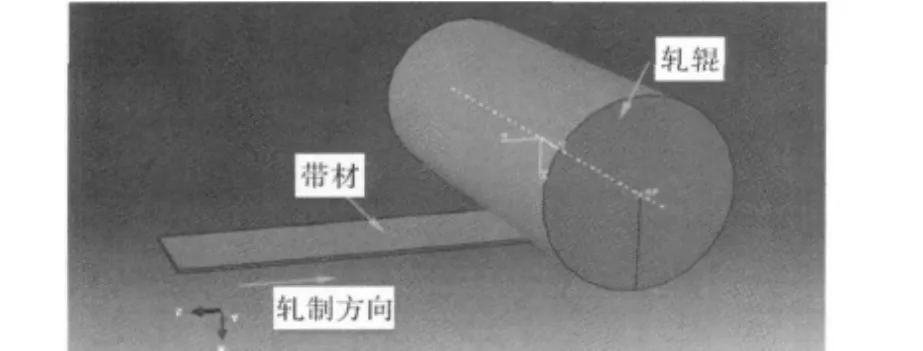
图1 铝合金冷轧过程三维有限元对称模型Fig.1 Three-dimentional finite element symmetry model in cold rolling process of aluminium alloy

为保证轧制过程的顺利进行，板材和轧辊采用过盈接触配合实现初始咬入［7］，待模拟稳定后，对比动能/内能曲线，保证动能与内能比值在10%以内。为保证计算结果的准确性，计算采用沙漏控制 (Hourglass control)，双精度计算模式。输出数据时，为保证结果准确性，数据点选取大于50个，取其平均值。

2 模拟分析

基于建立的有限元模型对轧制过程的Mises应力和等效塑性应变分布进行研究，在此基础上改变轧辊参数，研究不同轧辊直径和轧辊转速下应力和各应变分量之间的变化关系。

模拟中板材尺寸保持不变，板材宽度为30 mm，厚度2 mm，模拟过程中板材厚度压下率为50%。轧辊直径取Ф50 mm和Ф100 mm两种规格，轧辊转速选取如:对于Ф50 mm:轧辊转速选取38.2、76.4、152.8和191.0 r/min;对于Ф100 mm: 轧辊转速 19.1、38.2、76.4、95.5和191.0 r/min。这里部分轧辊转速为虚拟转速，仅作研究使用。

2.1 轧制过程Mises等效应力和等效应变分布

研究轧制过程Mises等效应力和等效应变分布可以对板材成形过程应力应变变化进行整体认识，同时也可以对改变轧辊参数下板材应力应变分布变化进行宏观把握，防止出现模拟不稳定情况。

图2给出了轧辊直径D=100 mm、转速ω=38.2转/分时板材轧制过程Mises应力分布，可以看出，轧制变形区内，轧制力沿宽度方向分布不均匀。最大Mises等效应力为223.8 MPa。板材宽向中部区域应力值大于边缘处，这是由于边缘处材料沿宽向不受约束自由流动导致的结果。其他轧辊参数下板材轧制过程Mises应力分布与图2基本相同，区别在于Mises应力大小。在相同压下量下，轧辊直径越大，Mises应力越大，轧辊转速越大，Mises应力越小。改变轧辊参数下，Mises应力变化范围在10～30 MPa。

图3所示为轧制过程中等效塑性应变(PEEQ)分布。可以看出等效塑性应变分布沿宽度方向呈不均匀分布，其中板材宽度中部等效塑性应变值大于边缘处。改变轧辊参数时，等效塑性应变变化范围为1.68～2.83。

图2 铝合金冷轧过程Mises等效应力分布(轧辊直径D=100 mm，转速ω=38.2转/分)Fig.2 Mises equivalent stress distribution in cold rolling process of aluminium alloy(D=100 mm;ω=38.2 RPM)

研究发现，不同轧辊参数下板材的应力分布基本相同，等效塑性应变差异较大。

图3 铝合金冷轧过程等效塑性应变分布(轧辊直径D=50mm，转速=38.2转/分)Fig.3 Equivalent plastic strain distribution in cold rolling process of aluminium alloy(D=50 mm;ω=38.2 RPM)

2.2 轧辊参数对应力分布影响

对比轧制变形区的各应力分量 (包括厚向应力、宽向应力和伸长应力)，分布基本相同，相差不大。以轧辊直径D=100 mm，转速ω=38.2转/分为例，模拟轧制过程，结果如图4所示。可以看出，轧制过程为三向压应力状态，厚向应力最大，伸长应力最小，为第一主应力。改变轧辊参数时，厚向应力变化范围为820～1063 MPa，宽向应力变化范围为710～943 MPa，伸长应力变化范围为529～924 MPa。

2.3 轧辊参数对应变分布影响

图5给出了轧辊参数对伸长应变的影响，可以看出，对于D50系列 (D=50 mm)，轧辊转速对伸长应变影响不大;对于D100系列 (D=100 mm)，轧辊参数对伸长应变分布影响较大。伸长应变分布于轧辊转速有关，当轧辊转速较低时 (19.1 r/min和38.2 r/min)，伸长应变呈“凹”字型变化，板材最大应变值出现在1/3宽度处，宽度中心部分的伸长应变低于1/3宽度处应变值;当轧辊转速大于76.4 r/min时，伸长应变呈梯形分布。

对比D50和D100，可以看出改变轧辊直径后，伸长应变发生较大变化，局部点处伸长应变相差可达17.9%。从板材厚度均匀性讲，增大直径和轧辊转速有利于提高厚度均匀性。

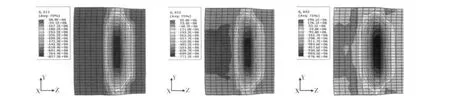
图4 轧制变形区应力分量分布示意图 (S11－厚向应力，S22－宽向应力，S33－轴向应力)Fig.4 Distribution of stress components in rolling deformation area(S11 is thickness direction stress;S22 is width direction stress;S33 is axial stress)

塑性成形过程中满足体积不变条件，即εt+εw+εl(εt、εw、εl分别表示厚向应变、宽向应变和伸长应变)，所以厚向应变 εt≈ －εw－εl，由于宽向应变较小，厚向应变近似等于伸长应变。有限元计算得到的不同轧辊参数下板材沿宽向厚向应变分布与伸长应变分布相似，本文不再赘述。

从图5可以看出，改变轧辊参数下，伸长应变分布存在三种形式:(1)“凹”字形;(2)梯形;(3)抛物线形。

轧辊参数变化引起应变分布的差异性可从轧辊接触面积和材料流动速度解释。

3 结论

基于铝合金冷轧过程有限元模型，研究不同轧辊参数对应力应变分布结果，得到结论如下:

图5 不同轧辊参数下板材沿宽向伸长应变分布Fig.5 Strain distribution of strip along width direction as roller parameter is different

(1)轧辊参数对Mises等效应力分布影响较小，对各应力分量的分布影响较小;轧辊参数对板材等效塑性应变影响较大，波动范围为1.68～2.83;

(2)轧辊转速对板材厚向应变、伸长应变的影响与轧辊直径相关，对于50 mm的辊径，轧辊转速对各应变值影响很小，应变呈抛物线形分布;对于100 mm的辊径，当轧辊转速小于76.4 r/min时，厚向应变、伸长应变呈“凹”形分布，当轧辊转速大于76.4 r/min时，应变呈梯形分布。

(3)改变轧辊直径后，厚向应变、伸长应变发生较大变化，局部点处应变相差可达17.9%。增大直径和轧辊转速有利于提高厚度均匀性。

［1］ I．J．Freshwater．Simplified theories of flat rolling-I．The calculation of roll pressure，roll force and roll torque ［J］．Int．J．Mech．Sci．1996，38(6):633－648．

［2］ Pierre Montmitonnet．Hot and cold strip rolling processes ［J］．Comput．Methods Appl．Mech．Engrg．2006，195:6604－6625．

［3］ 刘立忠，刘相华，王国栋．轧制过程的显示动力学有限元模拟［J］．力学与实践．2001，23:34－36．

［4］ 丁文华，李淼泉，姜中行，等．中厚板轧制过程的数值模拟［J］．轧钢．2010，27(6):15－21．

［5］ X．Duan，T．Sheppard．Three dimensional thermal mechanical coupled simulation during hot rolling of aluminium alloy3003 ［J］． Int． J． Mech． Sci．2002，44:2155－2172．

［6］ B．P．Gearing，H．S．Moon，L．Anand．A plasticity model for interface friction:application to sheet metal forming ［J］．Int．J．Plasticity，2001，17:237－271．

［7］ Zhijun Li，He Yang，Heng Li，et al．An accurate 3D-FE based radius prediction model for in-plane roll-bending of strip considering spread effects ［J］．Comput．Mater．Sci．2010，50:666 －677．