利用变压器箱体振动模型确定故障阈值

刘洪涛， 马宏忠， 高 鹏， 陈 楷， 王春宁， 李 凯

(1.河海大学能源与电气学院， 南京 210098；2.江苏省电力公司南京供电公司， 南京 210008)

利用变压器箱体振动模型确定故障阈值

刘洪涛1， 马宏忠1， 高 鹏1， 陈 楷2， 王春宁2， 李 凯2

(1.河海大学能源与电气学院， 南京 210098；2.江苏省电力公司南京供电公司， 南京 210008)

振动信号分析方法是一种通过测量和分析变压器箱体表面的振动信号来诊断变压器状态的技术。文中提出了一种通过箱体振动模型来确定故障阈值的新方法。根据变压器本体振动产生、传递的机理，以负载电压和负载电流为输入变量，建立了实用的变压器箱体振动预测模型，同时借助线性最小二乘法完成对变压器箱体振动故障阈值的确定。最后利用此振动模型预测了某负载和加载电压下的箱体振动故障阈值，并与实测信号进行了比较分析，验证了模型的有效性。

电力变压器； 振动分析； 振动模型； 最小二乘法； 故障阈值

变压器所有故障中有12%～15%是由短路时的高电动力导致绕组和铁芯变形而引起的[1]。这些几何变化使得绕组和铁芯振动加剧，其结果必然引起固体绝缘机械疲劳。长期如此，会导致固体绝缘受损，引起各绕组之间发生相间短路、匝间短路及接地短路等故障。另一方面，绕组变形使得导体间距离发生变化，串联和并联电容也随之变化，影响变压器的正常运行[2，3]。因此很有必要对变压器故障类型作出有效预测并及时处理。然而，由于变压器型号不同、环境不同，判别故障的阈值也不相同，所以需要一种通用性强的确定故障阈值的方法。

本文提出一种监测变压器油箱振动的模型，目的是为了确定变压器的故障阈值，同时还能预测一些早期故障。通过一些输入变量，该模型会计算出一些变压器的关键变量[4，5]。测量值和计算值之间的差距可反映变压器结构的变化。在给定的工作条件下，模型会计算出箱体振动的主要成分幅值大小。并以这些数据为基准，确定故障阈值的大小。

1 变压器振动分析

1.1 绕组振动分析及模型的建立

运行中的变压器绕组线圈可以看作一个受到外界激励的质量-刚度-阻尼机械振动结构，由于受到强大的电磁力(特别是超载或短路大电流引起的巨大电磁力)冲击，做着复杂的机械振动，整个绕组带动铁芯、绝缘垫块和夹件等结构发生振动，通过器身和油介质传递到变压器箱体表面，同时以声波的形式向外扩散。

绕组的振动是由于在漏感的影响下，线圈中的电流相互作用产生电动力引起的，电动力正比于电流的平方，而且在线圈的轴向和径向方向上形成分量。轴向力在竖直方向压缩绕组。对于一个普通的高低压绕组，由于电流在同一绕组中方向相同，导致径向力会压缩低压绕组(内部绕组)而向外拉伸高压绕组(外部绕组)。两绕组在轴向和径向的受力如图1所示，此图为俯视图，高低压绕组在中间，左右而居，绕组位置一侧为油箱，另外一侧为铁芯。而高低压绕组受力的相对幅值则是由绕组的高度和半径决定的[6]。

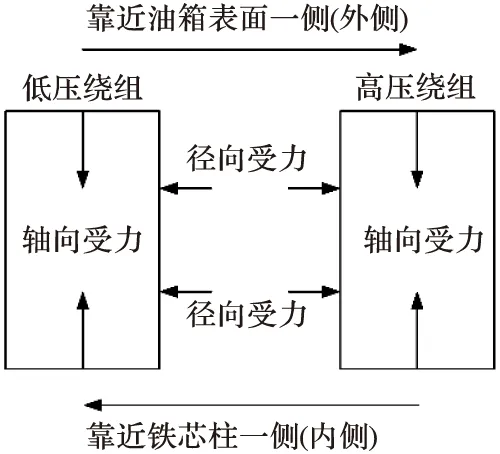
图1 绕组受力图

由于绕组的振动取决于负载电流的平方，即

vvinding∝i2

(1)

式中：vwinding表示绕组振动。

考虑到电流的频率等于电网频率50 Hz，因此绕组的主要谐波分量为负载电流频率的2倍，即100 Hz。

1.2 铁芯振动分析及模型的建立

铁芯振动是由磁致伸缩[7]和磁力引起的，当磁性材料被置入到磁场环境中时，会有相当数量的原子的尺寸发生形变而引起振动。图2描述了磁致伸缩形变与铁芯中磁通密度的关系曲线[8]，其中实线为实测的度量铁芯磁致伸缩大小(形变)与磁通密度之间关系的曲线图，它表示了在磁通密度变化的一个周期(正弦信号)内微小单元磁致伸缩的形变，可以看到磁致伸缩具有明显的磁滞现象规律，为了简化可以将其由二次曲线代替，如图2中虚线所示，这样简化之后可以使磁致伸缩引起的铁芯受力与磁通密度的平方确立线性关系[9，10]。

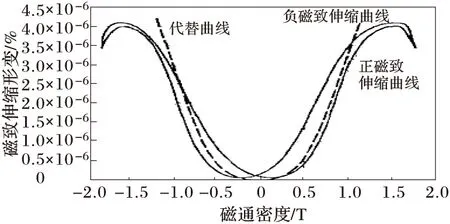
图2 铁芯磁致伸缩形变随磁通密度变化曲线

负载电压和磁通密度之间的关系为

(2)

式中：φ和B分别表示主磁通和磁通密度；A为铁芯的横截面积；U为负载电压的有效值；f对应负载电压的频率；N为原边线圈的匝数。由式(2)可知负载电压与磁通密度存在线性关系，结合图可以得到：

vcore∝u2

(3)

即铁芯所受磁致伸缩引起的振动力与负载电压之间存在正比关系。由于负载电压的2倍频为100 Hz，故与绕组所受电动力相同，磁致伸缩力的基频同样为100 Hz。理想情况下，磁致伸缩引起的振动只发生在均质铁磁体中，且局限于铁芯平面内，但由于铁芯是由许多硅钢片制成，而且在支撑和铁轭结合处硅钢片互相交叠在一起。在这种情况下，支撑和铁轭结合处难以避免地存在硅钢片间缝隙不均匀以及由此衍生的结点处层间磁通等现象，导致磁通密度的分布不规则。这种不规则会在垂直于铁芯的平面内产生附加的磁致伸缩现象。因此可以认为，铁芯的振动主要取决于硅钢片的磁致伸缩[11]。

2 绕组和铁芯模型的实验验证

对于以上绕组和铁芯的模型建立，主要是从理论分析的角度研究了变压器一些部件的振动特性。但这些分析是否与实际达到一致，绕组振动是否和电流平方成正比，铁芯振动是否和电压平方成正比，这还需要通过实验验证。

本文对实验室的一台三相实验用变压器进行了振动测试实验，该单相变压器为南京供电公司退役的变压器，额定功率为100 kVA，高压侧额定电压为10 kV，低压侧为400 V，结构完好。为了验证绕组振动和负载电流、铁芯振动和负载电压的关系，实验分别改变负载侧的电流和电压，从而获取不同的振动信号，通过曲线拟合方法，拟合出两者之间的关系。

2.1 实验验证绕组振动和负载电流的关系

在此实验过程中，负载时的振动是由绕组振动和铁芯振动叠加而成的。但如果负载电压较低，可以忽略铁芯的振动，因为在很低的负载电压下的磁致伸缩现象不明显，几乎可以忽略。这时，可近似认为变压器箱体振动主要由绕组引起。

接通电源后，调整负载大小，使得负载电流分别为额定电流的10%～50%中间的9组数据。同时采集记录不同的负载电流箱体上的振动加速度传感器信号。在各频域谱图中提取100 Hz处的幅值，建立与不同负载电流平方的关系。对离散点进行最小二乘法拟合得到箱体振动信号基频分量与负载电流的关系曲线。负载电流与振动加速度信号基频成分幅值之间的拟合关系如图3所示，拟合得到的曲线的线性方程为

V=2.706+1.11I2

(4)

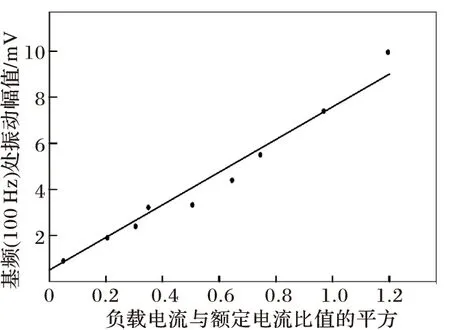
图3 箱体振动基频振动幅值与负载电流的关系

可以看出基频分量的大小基本与负载电流与额定电流的比值平方呈线性关系。验证了前面的模型推导。

2.2 实验验证铁芯振动和加载电压的关系

由上节的实验以及已有的理论分析可知，绕组振动主要是由负载电流引起的，所以当变压器空载时，变压器的振动可以认为是由铁芯受磁致伸缩产生振动并传递到箱体表面的。因此这时实验可以认为是空载实验。

将负载测处于开路状态，调节调压器按钮，使得空载电压分别为110%，100%，90%，80%，70%额定电压，同时采集和记录不同空载电压箱体上振动加速度传感器的信号。抽取基频100 Hz处的振动幅值，绘制基频振动与空载电压关系图，如图4所示，在图中离散点是通过实验获得的，对离散点进行最小二乘法拟合得到空载时箱体振动信号基频分量与负载电压的关系曲线。拟合得到的曲线方程为

V=0.46+7.25U2

(5)

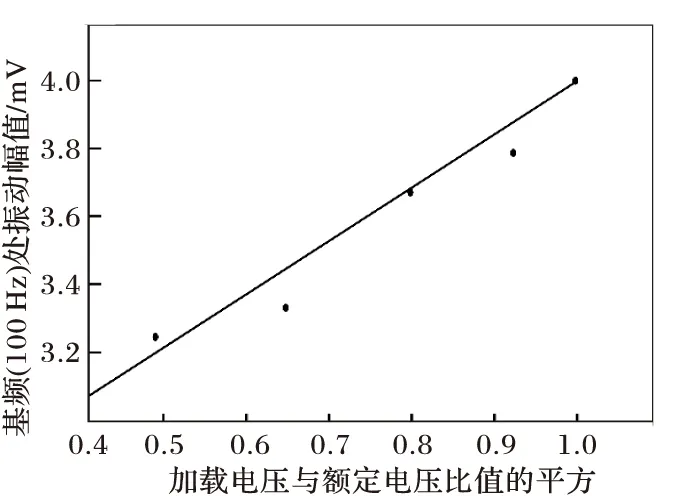
图4 箱体振动基频分量幅值与加载电压的关系

可以看出，空载时基频分量的大小基本上与输入电压与额定电压比值平方呈线性关系。

3 变压器箱体振动模型的建立

根据前面的分析，得到绕组振动幅值与负载电流的平方成正比，因此

vwind∝(I50cos(2πft+φu50,i50))2

(6)

其中，vwind为绕组振动幅值；I50为工频电流最大值；φu50,i50为负载电流与负载电压之间的相位角，取负载电压的初始相位为初相角。

同理，可以获得铁芯振动的表达式为

vcore∝(U50cos(2πft+φu50,i50))2

(7)

式中：vcore为铁芯振动幅值；U50为工频电压最大值。

这里需要指出的是，由于仅研究变压器箱体振动的基频成分，且磁致伸缩现象的强非线性使铁芯振动的高次谐波分量难以表述，故此式子对高次谐波分量不具有实际物理意义[12～16]。

而指定方向上的振动模型可以简化为

vtank=c1vwind+c2vcore

(8)

式中：vtank表示箱体振动；c1表示绕组振动系数；c2表示铁芯振动系数。

故将式(6)和(7)带入式(8)得到

(9)

需要指出的是负载电流信号中含有磁化电流谐波分量和部分冗余谐波电流分量，但是远远小于50 Hz的电流分量，负载电压的情况类似，因此本文为了简化模型，将上式写为

(10)

其中：I和U分别为负载电流信号和负载电压信号的有效值；而IN和UN则对应变压器的额定电流和额定电压。

下面进一步研究变压器箱体振动与模型输入之间的关系，并由此确定模型的参数。

将式(10)写为矩阵形式如下：

(11)

或者写为：

Vt=[LY]×C

(12)

式中：Vt为不同输入变量，箱体振动基频分量幅值计算值，模型的输出；L为负载电流标么值的平方，模型的输入变量；Y为负载电压标么值的平方，模型的输入变量；C为与负载电压和负载电流相关的系数，模型参数。

模型参数的辨识可以通过最小二乘法完成。最小二乘识别法就是以实验数据与理论模型的均方误差最小为准则识别未知参数的方法[17～20]，其数学模型为

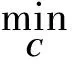
(13)

由于模型参数C表示绕组和铁芯的传递系数，因此为非负，故模型需要加上约束条件：

(14)

所以该问题变为非负线性最小二乘参数辨识问题。

为了训练和确定模型参数，同时保证模型参数可以准确刻画振动输入和输出变量之间的依赖关系，可以先获得稳定运行状态下的变压器，改变其外加电压和低压侧负载，然后获取不同的输入变量，在得到负载电流和加载电压信号后，首先求取二者的有效值，并求取有效值与额定值比值的平方，即模型的输入变量(liyi)，重复上述过程，获得输入变量矩阵[LY]。在采集负载电流和加载电压信号的同时，利用振动加速度传感器从箱体上采集箱体振动信号，得到模型输出的实测值。根据模型(13)并利用非负线性最小二乘法对模型进行参数辨识。

4 故障阈值的确定

当模型参数被确定后，该变压器箱体振动模型被用于计算任意负载和加载电压下箱体振动信号的基频分量幅值大小。通过比较某负载和加载电压下实测值和计算值的大小和误差，发现实测值和计算值有较好的吻合度。即可以通过此模型计算基频分量，这个分量，就是正常运行状态下的变压器振动基频分量，也是可以作为一个阈值标准。

在第2节实验验证中，本文采用了一台实验用变压器进行验证。在本节中依然使用同一台变压器进行实例分析。首先测取不同电压和电流下的振动幅值的大小，并汇总成表。

表1为从本台变压器得到的模型输入变量。

表1 模型输入变量

根据以上得到的不同电压电流条件下的基频幅值分量，可以利用公式(13)进行模型的参数辨识。求得该变压器的参数C1和C2。

表2为利用Matlab对模型参数辨识的结果，即对C1和C2的计算结果。

表2 模型参数辨识结果

当模型的参数被确定之后，该变压器箱体振动模型可以被用于计算任意负载和负载电压下箱体振动信号的基频幅值大小。根据公式(15)，可以求得不同条件下振动的基频幅值分量。

(15)

表3是在一定负载和加载电压下，变压器振动的计算值和实测值的大小，并对同一条件下的计算值和实测值进行误差分析。通过对比两者的大小及其误差，验证了该方法的有效性。

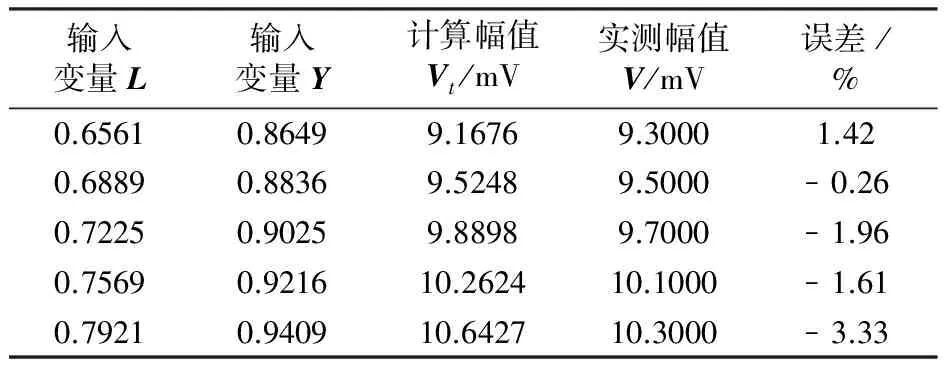
表3 变压器振动的计算值及实测值

通过比较实测值和计算值的大小和误差，发现实测值和计算值有较好的吻合度，且相对误差在可以接受的范围内(5%).故本文所提出的模型可以计算变压器振动的基频分量，即可以当作振动故障的阈值标准。

5 结语

本文介绍了利用变压器箱体振动模型确定故障阈值的方法，通过研究表明，利用变压器箱体振动模型对基于振动的变压器故障诊断的阈值确定结果是可行的，较已有的方法优势明显，并且此方法不必建立箱体振动的数据库，避免大量振动信号的存储和管理，同时故障变压器的振动实测值与模型预测值差别明显，有利于故障定性。但此方法对变压器型号、温度及变压器其他部位振动的干扰考虑较少，所以对于模型参数来讲，还有很多的研究要做。

[1] Kirtley J L Jr, Hagman W H, Lesieutre B C,etal. Monitoring the health of power transformers [J]. IEEE Computer Applications in Power, 1996, 9(1): 18-23.

[2] Berler Z, Golubev A, Rusov V,etal. Vibro-acoustic method of transformer clamping pressure monitoring [C]∥ Conference Record of the IEEE International Symposium on Electrical Insulation, Anaheim, USA: 2000.

[3] 汲胜昌，刘味果，单平，等(Ji Shengchang, Liu Weiguo, Shan Ping,etal). 变压器铁心及绕组状况的振动测试系统(The vibration measuring system for monitoring core and winding condition of power transformer)[J]. 高电压技术( High Voltage Technology),2000, 26(6):1-3.

[4] Kwon H. Model of the Vibration of Power Transformer [D]. Seoul: School of Electrical Engineering of Soongsil University,1993.

[5] 谢坡岸，饶柱石，朱子述(Xie Po'an, Rao Zhushi, Zhu Zishu). 大型变压器绕组有限元建模与分析(Finite element modeling and analysis on transformer wingdings)[J]. 振动与冲击(Journal of Vibration and Shock), 2006,25(2):134-137,191.

[6] 何定，王磊，董昕，等(He Ding, Wang Lei, Dong Xin,etal).用于变压器故障诊断的ANNES(ANNES used for transformer fault diagnosis) [J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA),1994,6(3):1-7.

[7] 顾晓安，沈荣瀛，徐基泰(Gu Xiao'an, Shen Rongying, Xu Jitai). 大型电力变压器振动和噪声控制方法研究(Study on the vibration and noise control techniques in large power transformers)[J]. 噪声与振动控制(Noise and Vibration Control), 2001,21(5):7-11.

[8] Bozorth R M. Ferromagnetism [M]. New York: IEEE Press,1993.

[9] 顾晓安，沈密群，朱振江，等(Gu Xiao'an, Shen Miqun, Zhu Zhenjiang ,etal). 变压器铁心振动和噪声特性的试验研究(Test research on vibrations and noise level in transformer core)[J]. 变压器(Transformer), 2003, 40(4):1-4.

[10]顾晓安，沈荣瀛，许庆新，等(Gu Xiaoan, Shen Rongying, Xu Qingxin,etal). 铁磁质在磁场中所受磁场力的数学模型(Mathematical model of magnetic forces in ferromagnetic materials under magnetization)[J].上海交通大学学报(Journal of Shanghai Jiaotong University),2003, 37(5):794-797.

[11]杨淑英，赵凯(Yang Shuying, Zhao Kai). 基于FTA法的变压器故障分析(Transformer faults analysis based on FTA)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(3):96-99.

[12]Garcia B, Burgos J C, Alonso A M. Transformers tank vibration modeling as a method of detecting winding deformations-part I: theoretical foundation [J]. IEEE Trans on Power Delivery, 2006, 21(1): 157-163.

[13]Garcia B, Burgos J C, Alonso A M. Transformers tank vibration modeling as a method of detecting winding deformations-part II: experimental verification[J]. IEEE Trans on Power Delivery, 2006, 21(1): 164-169.

[14]Leibfried T, Feser K. Monitoring of power transformers using the transfer function method[J]. IEEE Trans on Power Delivery, 1999, 14(4): 1333-1341.

[15]Bartoletti C, Desiderio M, Di Carlo D,etal. Vibro-acoustic technique to diagnose power transformers [J]. IEEE Trans on Power Delivery, 2004, 19(1): 221-229.

[16]Birlasekaran S, Fetherston F. Off/on-Line FRA condition monitoring technique for power transformer [J]. IEEE Power Engineering Review, 1999, 19(8): 54-56.

[17]陆健(Lu Jian). 最小二乘法及其应用(The least square method and its application)[J]. 中国西部科技(Science and Technology of West China), 2007, 5(19):19-21.

[18]刘志平，石林英(Liu Zhiping, Shi Linying). 最小二乘法原理及其MATLAB实现(The principle of least square algorithm and its achievement by MATLAB)[J]. 中国西部科技(Science and Technology of West China), 2008,6(17):33-34.

[19]石贤良，吴成富(Shi Xianliang, Wu Chengfu). 基于MATLAB的最小二乘法参数辨识与仿真(Rls parameter identification and emulate based on Matlab/Simulink)[J]. 微处机理(Microprocessors),2005,21(6):44-46.

[20]邱英(Qiu Ying). MATLAB在线性参数最小二乘法处理中的应用(Application Matlab in least square method with liner parameter)[J]. 科技广场(Science Mosaic), 2007, 25(5):165-166.

刘洪涛(1986-)，男，硕士研究生，研究方向为电气设备状态检测与故障诊断。Email:513971301@qq.com

马宏忠(1962-)，男，教授，博士生导师，研究方向为电气设备状态检测与故障诊断、电力系统远程监控与继电保护、新能源发电等。Email:hhumhz@163.com

高 鹏(1986-)，男，硕士研究生，研究方向为电气设备状态监测与故障诊断。Email:hehaixiaoxue@163.com

MethodofDeterminingtheThresholdofTransformerFaultUsingTransformerTankVibrationModel

LIU Hong-tao1， MA Hong-zhong1， GAO peng1， CHEN Kai2， WANG Chun-ning2， LI Kai2

(1.College of Energy and Electrical Engineering, Hohai University, Nanjing 210098, China；2.Nanjing Power Supply Company, Jiangsu Electric Power Company,Nanjing 210008, China)

The vibration signal analysis is a kind of technique to diagnose transformer's condition through measuring and analyzing vibration signal from the tank surface. This paper proposes a new method of determining the threshold through vibration model of transformer tank. A vibration prediction model of transformer tank is built using the mechanism of generation and transmission of vibration with on-load voltage and load current as inputs. Meanwhile, least squares method is used to determine the threshold of transformer fault. Finally, this model is used to predict a testing fault threshold in a specific situation. Through the comparison of actual and predicted threshold, the conclusion can be drawn that this method is very effect in the field of determining the threshold of transformer fault.

transformer； vibration analysis； vibration model； least squares method； fault threshold

TM41

A

1003-8930(2012)06-0036-05

2011-10-17；

2011-11-30

国家电网公司科技项目资助(2011-0810-2251)