残余应力对焊接中厚板频率的影响分析

陶承伟，张系斌，刘焕玉 (长江大学城市建设学院，湖北 荆州 434023)

残余应力对焊接中厚板频率的影响分析

陶承伟，张系斌，刘焕玉 (长江大学城市建设学院，湖北 荆州 434023)

通过大型有限元分析软件ANSYS，在2边简支和4边简支边界条件下，分别得出其前10阶频率，对比分析焊接残余应力对中厚板频率的影响。结果表明，在2边简支和4边简支边界条件下，有残余应力比无残余应力的中厚板的频率小，但是相差不大；相同规格中厚板、4边简支边界条件下频率值较2边简支边界条件下各阶相应频率值大；在相同边界条件下，无残余应力和有残余应力中厚板随着板厚的增加其频率均相应增大,而频率差率却逐渐减小，当板厚增加到一定厚度时，可不计焊接残余应力对中厚板频率的影响。

中厚板；焊接残余应力；频率

随着经济的飞速发展，中厚板在国防、交通运输、能源和建筑等各种重要的国民经济部门被广泛应用[1]。很多学者对焊接残余应力进行了广泛而深入的研究，但是对于焊接残余应力对中厚板频率的影响研究还不多见。焊接残余应力将直接影响构件的受力性能，降低构件的刚度和临界荷载，对中厚板频率等产生不可忽视的影响。为此，笔者利用有限元分析方法，分析焊接残余应力对中厚板频率的影响。

1 模态分析理论

用有限单元法分析结构振动问题以及动态响应问题，即在动荷载作用下分析物体的应力、变形问题时，动力学问题有限单元法需把物体离散为有限个数的单元体[2]。具有粘性阻尼的自由度系统振动微分方程如下[3]：

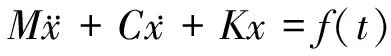
(1)

粘性阻尼矩阵C一般不能利用模态矢量的正交性对角化，故不能应用坐标变换直接将式(1)解耦。但在特殊情况下C可利用正交性对角化，如Rayleigh提出的粘性比例阻尼模型[3]：

C=αM+βK

(2)

式中，α、β分别为与系统外、内阻尼有关的常数。

令f(t)=0,C=0,则式(1)变为：

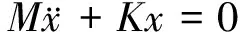
(3)

设特解：

x=Φejω t

(4)

式中，Φ为自由响应幅值列阵,ω为频率；t为时间。

将式(4)代入式(3)，得到以Φ中元素为变量的n阶代数齐次方程：

(K-ω2M)Φ=0

(5)

式中，K-ω2M为其系数矩阵。

按自由振动理论，n阶自由度系统的自由振动方程式应有n个固有频率ωi(i=1,2,…,n)，即：

|K-ω2M|=0

(6)

求得ω后，再将ω代入式(5)即可求出特征振动模态Φ。

2 有限元分析

2.1材料工艺参数

模拟焊缝采用高斯热源作为焊接热源模型，中厚板的类型分为2组，1组为无残余应力的中厚板；另1组为有残余应力的中厚板；中厚板尺寸分别为 12mm×80mm× 150mm、 16mm× 80mm×150mm和20mm× 80mm×150mm，材质采用Q345B，其具有良好的机械性能、可焊性和加工工艺性。焊接方式为CO2气保护焊，坡口角度为45°，分4道焊；抗拉强度σb为490～665MPa，屈服强度σs≥325MPa，伸长率δ5≥21%，冲击度20；采用具体焊接参数如下: 焊接电流为170～550A，焊接速度为5mm/s，焊丝采用直径为4mm的H10Mn2焊丝。

2.2有限元模型的建立

在焊接过程ANSYS数值模拟过程中，拟采用PLANE13和SOLID5单元，其中PLANE13平面单元用于焊缝横截面的网格划分，SOLID5为PLANE13面单元拖拉成体方式生成的三维实体单元。这2种单元相互对应，同阶且具有相同的自由度。PLANE13和SOLID5单元均为结构和热耦合单元，在应力分析中，不需要再次转换单元，能一次性完成热结构耦合的分析计算。但在前处理中划分面的网格后要进行单元转换，即把PLANE13单元转换为SOLID5单元。由于假设焊条与母材材料性能的一致性，因此焊缝和母材均采用SOLID5单元。焊缝处的网格长度控制为4mm，母材的网格尺寸适当加大为10mm。焊接中厚板的三维模型简图和三维对接焊缝有限元模型分别如图1和图2所示。

图1 焊接中厚板三维模型简图

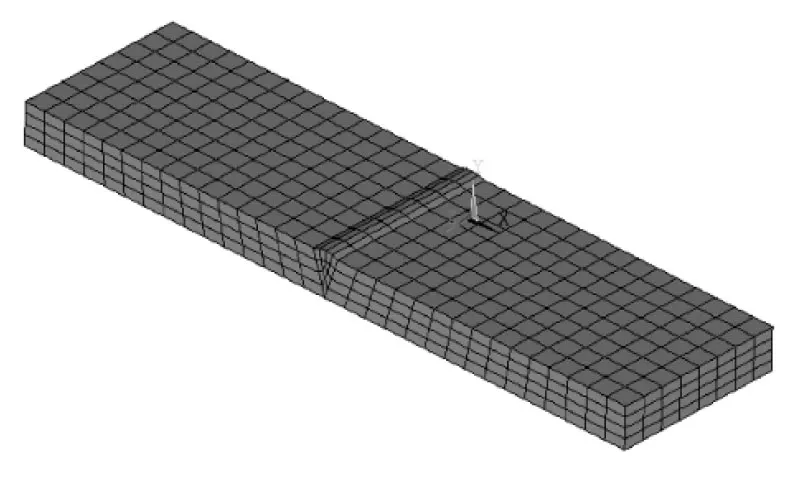
图2 三维对接焊缝有限元模型

2.3频率分析

对板厚为12、16和20mm的无残余应力中厚板和有残余应力中厚板分别在不同的边界条件下进行频率分析，并在不同边界条件下对各阶频率进行比较。考虑到该模型收敛速度和计算精度, 利用子空间迭代法进行模态分析，并采用波前求解器。对比分析无残余应力中厚板和有残余应力中厚板的前10阶频率。2边简支和4边简支边界条件下无残余应力中厚板和有残余应力中厚板的频率值分别如表1和表2所示。

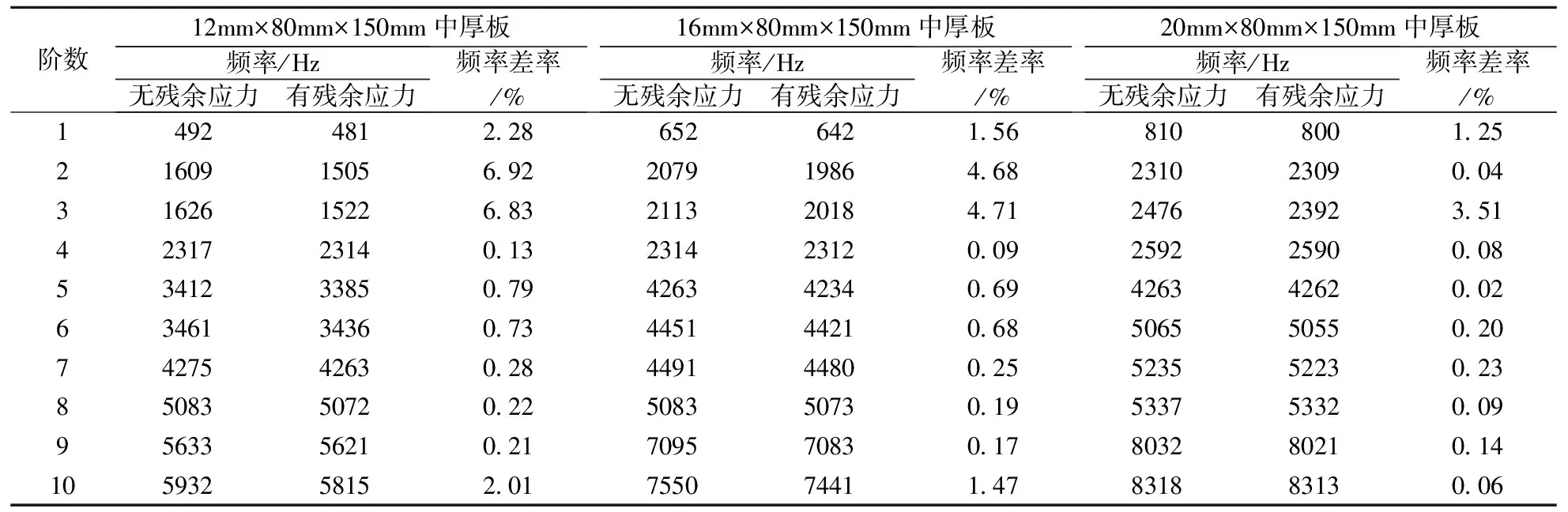
表1 2边简支边界条件下中厚板的频率值

表2 4边简支边界条件下中厚板的频率值

从表1和表2 可知，在2边简支和4边简支的边界条件下，板厚为12mm、16mm以及20mm的有残余应力中厚板各阶频率比相应的无残余应力中厚板各阶频率小，但各阶频率差值不大。2边简支边界条件下进行不同宽厚比的中厚板频率对比分析，可知无残余应力和有残余应力频率差最大百分比为6.92%；4边简支边界条件下进行不同宽厚比的中厚板频率对比分析，可知无残余应力和有残余应力频率差最大百分比为6.67%；2种边界条件下频率差最大百分比均不到7%。

由2边简支和4边简支边界条件下的频率对比分析可知，随着约束的增加，4边简支边界条件下无残余应力和有残余应力中厚板频率均比2边简支边界条件下相应的各阶频率大。

3 结 论

1)在相同边界条件下，有残余应力中厚板比无残余应力中厚板的相应的各阶频率小，但差值不大；随着板厚的增加，焊接中厚板与非焊接中厚板的各阶频率差异可忽略不计。

2)相同尺寸的中厚板，4边简支边界条件下比2边简支边界条件下各阶相应频率值大。

3)在2边简支和4边简支的边界条件下，焊接残余应力对中厚板频率差率的影响随着板厚的增加而减小，当板厚增加到一定厚度时，可不计焊接残余应力对中厚板频率的影响。

[1]陈永利，罗登，杨来铭，等. 中厚板市场的发展现状及趋势[J]. 钢铁研究学报, 2009,21 (7) :22-24.

[2]王国强. 实用工程数值模拟技术及其在ANSYS上的实践[M] . 西安: 西北工业大学出版社, 1999.

[3]张力，林建龙，项辉宇，等. 模态分析与实验 [M] . 北京: 清华大学出版社, 2011.

[编辑] 李启栋

10.3969/j.issn.1673-1409(N).2012.02.037

TU375.2； TG404

A

1673-1409(2012)02-N113-03

2011-11-18

陶承伟(1986-)男, 2009年大学毕业, 硕士生，现主要从事结构工程方面的研究工作。