函数极值在经济管理中的应用

姜 雪

(沈阳工业大学 基础部，辽宁 辽阳 111003)

函数极值在经济管理中的应用

姜 雪

(沈阳工业大学 基础部，辽宁 辽阳 111003)

运用极值理论，从经济管理决策中常遇到的需求分析问题、利润最大化问题、库存管理问题、成本最小化问题和复利问题着手，通过具体实例对导数等相关知识在经济中所表示的的实际意义进行了阐述和说明。

极值;经济管理;成本函数

0 引言

高等数学是经济管理类专业的重要课程之一，是学习专业课的必备知识，对学生思维的训练和能力的培养起着至关重要的作用。然而，受传统教学的影响，大部分学生对数学的感觉是枯燥的、无用的，不同程度的带有一定的抗拒心理，导致了在运用数学工具来解决实际的经济问题时，由于数学基础不牢固而显得束手无策。所以新时代下的教学要彻底改变学生的思维意识，让学生切身体会到数学的实用性，从而自觉地去学习。引导其应用数学知识及相应理论去解决实际的问题［1－4］无疑是很好的途径之一，文中以极值在经济管理决策中常遇到的需求分析问题、利润最大化问题、库存管理问题、成本最小化问题和复利问题等着手［5－6］，引用实例进行了说明。

1 极值的定义

设函数f(x)在区间(a，b)内有定义，x0∈(a，b).如果在x0的某一去心邻域内有f(x)＜f(x0)，则称f(x0)是函数f(x)的一个极大值；如果在x0的某一去心邻域内有f(x)＞f(x0)，则称f(x0)是函数f(x)的一个极小值。

2 经济管理中的应用

2.1 需求分析

恩格尔(Engel)函数:商品的需求量同商品的价格，消费者的收入情况及地域差别等诸多因素具有相关性。若考虑将消费者的收入定为主要因素，视其他因素固定，则商品需求量依消费者收入变化的函数关系称为恩格尔函数，记为Q=f(x)(Q为需求量，x为消费者收入)。

明它的经济学意义。

2.2 最大利润

2.2.1 产量由生产商规定的最大利润

设R(x)和C(x)均表示可导函数，分别为总收入和总成本函数(x表示产量)，称R'(x)为边际收益

函数;C'(x)为边际成本函数。

总利润可表示为L(x)=R(x)－C(x)，欲使总利润最大，其一阶导数等于零，即

这表明:总利润最大时边际收益等于边际成本。

从(1)式与(2)式可知，边际收益等于边际成本时，是获得最大利润的产量处。同时若有边际收益对产量的微商小于边际成本对产量的微商，则该产量也能获得最大利润。

2.2.2 生产商规定价格下，需求关系决定生产量下的最大利润

将产量看作价格P的函数x=φ(P)，总收入函数为R=R(x)=x·P=Pφ(P)，

总成本函数为C=C(x)=C(φ(P))，在价格为P时的总利润为L=R－C=P·φ(P)－C(φ(P))，欲达到总利润最大，根据极值的充分条件需满足:

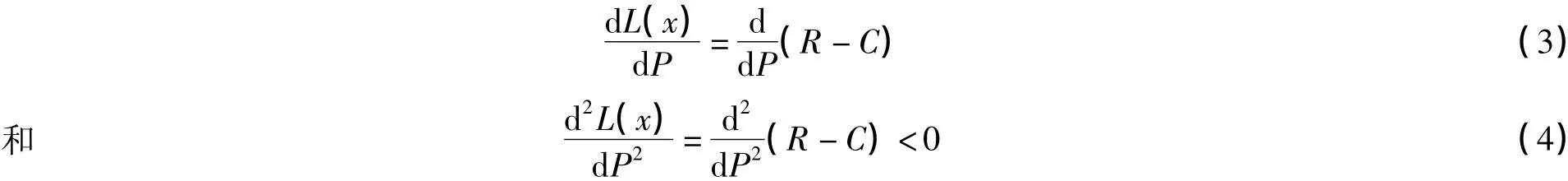
最优产量将由x=φ(P)确定。

例2.某农场有50间独立鸡舍要出租，当租金定为每月2000元时，鸡舍会全部租出去.当租金每月增加100元时，就有一间鸡舍租不出去，而租出去的鸡舍每月需花费200元的维护费.试问租金定为多少可获得最大收入?

解:设租金为每月x元，获得的收入为y，则有

所以，每套公寓租金定为3600元，可获得最大收入，最大收入为115600元。

2.3 库存管理

企业只有保证进行正常生产所必须的材料，才能完成生产任务。而材料需要一定的保管费用，在总需要量一定的条件下，订购批量和订购次数直接影响费用。订购批量小、订购次数多，保管费就少。因此如何确定订购批量使总费用最少的问题成为库存管理的主要问题之一。这里以整批间隔进货为例来讨论。整批间隔进货是指某物资的库存量下降到零时，随即订货、到货，库存量由零恢复到最高库存量Qmax，在每天保证等量供应生产需要，使之不发生缺货。

例3.设某快餐店每年对一次性餐具的需求量为40000套，每套餐具价格为2元，年保管费10%，每次订购的费用10元，试求最优订购批量、最优订购次数、最优进货周期和最小总费用。

解:设订货批量为Q，进货周期为T，总费用为C，则全年订购次数为

2.4 成本最低的生产量问题

生产实际中，常会研究在既定的生产规模及其相应的条件下，如何使成本最低，保证利润最大的问题。

例4.设某企业生产某产品的成本函数为C(x)，求平均成本最小的生产量水平。

解:由题意知，边际成本为C'=C'(x)，

由极值存在的必要条件知道，使平均成本为极小的生产量x0应满足g'(x)=0，故C'(x0)=g(x0)这表明:使得平均成本为最小的生产水平正是使得边际成本等于平均成本的生产水平。

2.5 复利问题

例5.某企业根据现有技术与资源条件，原计划所作投资使今年所得为x元，明年所得为y元，y与x满足:y=φ(x)，设年利率为r，每年计算复利一次，那么该厂应如何调整投资，使所得的现值最大?

由于1+r＞0，当φ″(x)＜0，即φ(x)为上凸函数时，可调整投资使今年所得的x满足φ'(x)=－(1－r)，这时，明年所得y可由y=φ(x)算出。

［1］ 葛云飞，李云友.高等数学教程［M］.北京:北京交通大学出版社，2006.

［2］ 周学勤.例说导数的应用［J］，牡丹江教育学院学报，2009，3(1):12－16

［3］ 彭文学.经济数学基础［M］.武汉:武汉大学出版社，2007.

［4］ 顾静香.经济应用数学［M］.北京:高等教育出版社，2007.

［5］ 滕勇，史俊贤.大学数学［M］.北京:高等教育出版社，2010.

［6］ 同济大学数学系.高等数学［M］.北京:高等教育出版社，2007.

The Application of Function Extremum in Economic Management

JIANG Xue

(Department of Basic Course，Shenyang University of Technology，Liaoyang 111003，China)

Based on extreme value theory，this paper，starting from the problems of demand analysis，profit maximum，inventory management，cost minimum and compound interest，discusses and explains the practical meaning of derivative and relevant knowledge in economy through some examples.

extremum;economic management;cost function

F224.9

A

1009－3907(2012)08－0986－03

2012-05-09

姜雪(1978-)，女，黑龙江明水人，讲师，硕士，主要从事教学方法，生物数学方面的研究。

责任编辑:程艳艳