DIF值和样本量对SIBTEST检测方法的影响研究

朱乙艺 韦小满

1 引言

近年来，项目功能差异（differential itemfunctioning，简称DIF）是心理与教育测量领域的一个研究热点。到目前为止，有很多的方法可以用于检测DIF，检测DIF的方法包括MH方法、STND方法、LRDIF方法、基于IRT的方法、MIMIC方法和SIBTEST方法等。不同的DIF检测方法的检验力（即正确识别率）是不尽相同的，即便对于特定的某种检测方法而言，其检验力也不是固定不变的，有一系列因素影响着其检验力。影响DIF检测方法检验力的因素包括样本量、测验长度、被试的能力分布、DIF项目的比例、DIF值的大小等。国外学者对这些检测DIF的方法进行了很多比较研究，也做了很多探讨这些检测方法的影响因素的研究。通过这些研究，国外学者探讨了各种DIF检测方法的效率及优缺点，为实践者选择合适的DIF检测方法提供了很好的依据。在国外学者的启发下，我国学者利用现实存在的成就测验数据进行了一些DIF检测方法的比较研究，也对影响DIF检测方法的因素进行了研究。董圣鸿等认为采用1000人左右的样本进行DIF分析是完全可取的，如果要更为谨慎的话，那么选用2000人左右的样本就可以了[1]。李付鹏以某年度6000名考生普通高考文科综合选择题的作答数据为样本，探讨了能力水平分组对MH方法检验敏感性的影响[2]，研究结果表明：不同能力水平分组的检验结果均具有较好的一致性；检验结果对能力水平分组组数的敏感性较小，MH方法具有较好的稳定性。

应该说，国内对DIF检测方法的研究有助于对国外的相关研究结论进行验证，是对DIF检测方法研究的有益补充。但是国内的研究基本上都是基于实测数据，这就决定了国内的研究和国外的模拟研究相比存在以下两点不足：

第一，国内的研究由于基于实测数据，所以只能在实测数据的基础上对变量进行一定程度的操纵。例如，从现有的样本中随机抽取一定比例的被试从而实现对样本量的操纵，但是诸如被试的能力分布、测验长度等变量则无法自由进行操纵。

第二，国内的研究由于是利用实测数据，因而无法事先知道哪些题目存在DIF，所以无法给出检验力和I型错误（即错误接受率）指标，只能进行相对的比较。在方法的比较研究中，国内的研究一般会观察若干种检测方法共同检测出来的题目个数和每种方法各自检测出来的题目个数，然后进行相对比较，显而易见，这样的相对比较是存在问题的，因为检测出来的题目并不一定是事实上存在DIF的题目，有可能是错误标记为DIF的题目。在方法的影响因素研究中也存在类似的问题，由于事先不知道哪些题目存在DIF，所以无法分离正确识别的题目和错误接受的题目。

因此，为了能够自由地操纵实验变量并且给出令同行信服的检验力和I型错误指标，国内的学者有必要基于模拟数据进行DIF检测方法的研究。本研究探讨了DIF值和样本量对SIBTEST检测方法的影响效应，以期一方面探明DIF值和样本量对SIBTEST检测方法的检验力和I型错误之间的关系，另一方面为国内学者未来开展模拟研究时选取DIF值提供参考。

2 SIBTEST方法概述

SIBTEST方法（Simultaneous Item Bias Procedure）是由Shealy和Stout于1993年提出的一种DIF检测方法。SIBTEST方法采用潜在能力作为匹配变量，用回归校正方法来估计匹配分数（Bolt&Stout，1995）。SIBTEST方法的DIF指标为[3]：

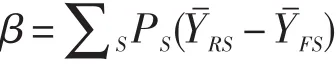
其中，PS为第S能力水平组中答对该项目的人数比率，、分别是第S能力水平组中参照组和目标组被试在该题上的平均得分。

SIBTEST还包括一个显著性检验：Z=β/σ（β）来检验项目的功能差异量是否显著：

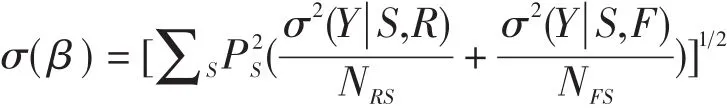
其中，σ2（Y|S，G）是匹配测验分数为S的G组（G=R或F）被试在所研究的项目上得分的方差。Z近似于N（0，1）的正态分布（Hua-Hua Chang&Jhon Mazzeo，1996），如果Z大于1.96或小于-1.96时（α=0.05，双侧检验），则拒绝零假设，即认为该项目存在DIF。

SIBTEST设计了一个迭代程序，把被怀疑存在功能差异的项目排除在匹配标准之外。此外，SIBTEST不仅可以对单个项目进行项目功能差异检验，还可以对一批项目进行项目束功能差异检测[4]。

3 研究方法

3.1 数据产生

题目的作答数据是利用三参数逻辑斯蒂克项目反应模型（3PLM）来产生的，在该模型中，单维能力为θ的被试正确作答题目i的概率为：

其中，ai为题目i的区分度参数，bi为题目i的难度参数，ci为题目i的伪猜测系数，D为量尺化系数（一般取D=1.7）。

难度参数b是从N（0，1）正态分布中随机选取的，区分度参数a是从N（0.5，0.2）正态分布中随机选取的，伪猜测系数c设定为0.2，具体的题目参数见表1。能力θ是从N（0，1）正态分布中随机选取的。测验的长度为40，即测验包含40道题目。

两级记分的题目作答数据是通过以下的过程得到的：首先通过上面的方程分别计算每个被试在每道题目上的正确作答概率，然后从U（0，1）一致性分布中随机选取一个数字，如果该数字小于Pi（θ），则将该被试在题目i上的作答记为1，如果该数字大于Pi（θ），则将该被试在题目i上的作答记为0。

目标组和参照组的能力分布均为N（0，1）正态分布，即目标组和参照组的能力是一致的。选取第5题来产生DIF，第5题的难度为-0.208，为中等难度；区分度为0.808，为中等区分度。DIF的引入是通过改变目标组的题目难度参数来实现的，即有利于参照组的DIF项目是通过bF=bR+来产生的。

表1 用来产生题目作答数据的参照组的题目参数

3.2 研究设计

本研究操纵了两个变量：DIF值和样本量。DIF值指的是目标组和参照组的DIF项目的项目反应函数之间的面积，DIF值包含6个水平，分别是0.24、0.32、0.40、0.48、0.56和0.64，在产生DIF项目时对应的Δb分别是0.3、0.4、0.5、0.6、0.7和0.8。样本量包含6个水平，分别是250、500、1000、2000、5000、7000。因此，总共有6×6=36种条件，每个条件产生100个复本。

3.3 分析过程

SIBTEST方法的DIF检测是通过William Stout和Louis Roussos开发的SIBTEST软件[5]来进行分析的，判定题目存在DIF的标准是p＜0.05，分析过程中分别记录每种条件下的检验力和I型错误。

4 研究结果

在本研究中，SIBTEST方法检测结果的检验力的操作定义是在100个复本中第5题被标记为存在DIF的比例。Cohen（1988）提出在0.05显著性水平上如果检验力＞0.80则可以认为检验力是充分的[6]。

从表2中可以看出，当DIF值较小时（0.24和0.32），在样本量小于2000时，SIBTEST方法的检验力随样本量的增大而增大，当样本量大于等于2000时，检验力达到最大值，不再随着样本量的增大而增大；当DIF值为中等大小时（0.40、0.48、0.56），在样本量小于1000时，SIBTEST方法的检验力随样本量的增大而增大，当样本量大于等于1000时，检验力达到最大值，不再随着样本量的增大而增大；当DIF值很大时（0.64），当样本量大于等于500时，检验力达到最大值，不再随着样本量的增大而增大，样本量对SIBTEST方法的检验力的影响可以忽略不计。

表2 不同DIF值和样本量条件下SIBTEST方法的检验力

表2显示，当样本量小于等于500时，SIBTEST方法的检验力随着DIF值的增大而增大；当样本量为1000时，在DIF值较小时（0.24和0.32），SIBTEST方法的检验力随着DIF值的增大而增大，当DIF值达到中等大小以后，SIBTEST方法的检验力达到最大值，不再随着DIF值的增大而增大；当样本量大于等于2000时，SIBTEST方法的检验力均为最大值。

在本研究中，SIBTEST方法检测结果的I型错误的操作定义是不存在DIF的项目被错误地标记为存在DIF的比例，根据Bradley（1978）提出的严格、保守的检测结果稳健标准，如果I型错误介于0.025到0.075之间，那么可以认为检测结果是稳健的[7]。

从表3可以看出，在所有的DIF水平上，当样本量大于等于2000时，SIBTEST方法的I型错误随着样本量的增大而增大，而样本量小于2000时，SIBTEST方法的I型错误的变化与样本量的变化没有明显的关系。

表3显示，当样本量小于等于1000时，SIBTEST方法检测结果的I型错误的变化与DIF值的变化没有明显的关系；当样本量大于等于2000时，I型错误大致随着DIF值的增大而增大。

5 讨论

5.1 DIF的产生方法

在以往的模拟研究中，基于研究者对DIF产生原因的理解差异，模拟研究中DIF的产生一般有两种思路：第一种思路是基于单维的项目反应理论模型，通过改变目标组的题目参数来引进DIF；第二种思路是基于多维的项目反应理论模型，没有DIF的题目只测量首要维度，存在DIF的题目除了测量首要维度外，还测量到了其他维度。现有的大多数DIF模拟研究是采用第一种思路来产生DIF的，研究者们倾向于采用第一种思路是因为目前单维的IRT理论较为稳健，前人用该思路来产生DIF积累了很多宝贵的经验，用该思路来产生DIF操作较为简单。另一些研究者倾向于采用第二种思路的原因是他们认为多维测验更符合实际情况，并且认为通过引入新的维度来产生DIF是更为合理的。鉴于技术操作上的考虑，为了保证本研究的可行性，采用第一种思路来产生DIF。在第一种思路下，研究者一般根据其需要选取某种项目反应理论模型（Rasch模型、单参数逻辑斯蒂克模型、两参数逻辑斯蒂克模型或三参数逻辑斯蒂克模型），然后通过改变目标组的难度参数或者同时改变目标组的难度参数和区分度参数来产生DIF。本研究采用三参数逻辑斯蒂克模型来产生作答数据。

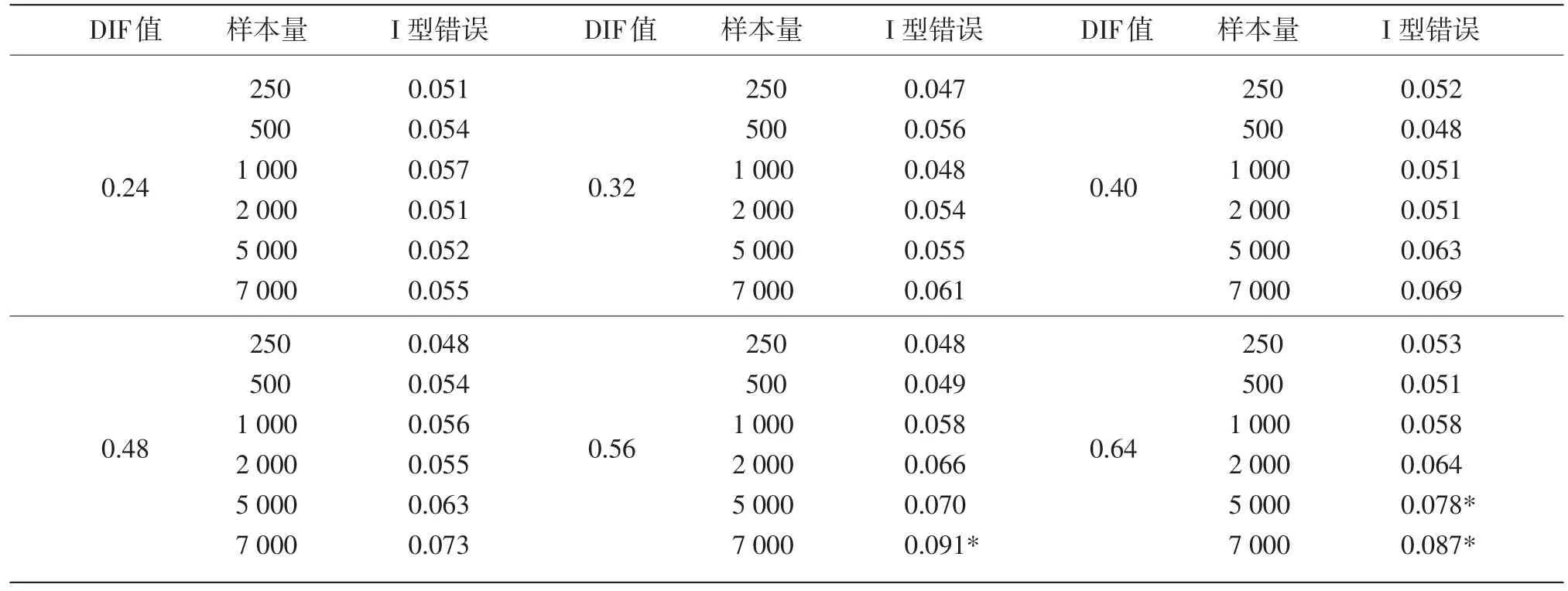
表3 不同DIF值和样本量条件下SIBTEST方法的I型错误

5.2 样本量和DIF值对SIBTEST方法的影响

样本量是DIF检测效果的重要影响因素之一，通过设置不同样本量的实验条件来探讨样本量对SIBTEST检测方法的影响具有重要的理论意义和实践意义。基于第一种思路来产生DIF时，采用多大的DIF值是一个值得认真考虑的问题。当用某种DIF检测方法对模拟的数据进行检测时，DIF值设置得过小或者过大，都可能对DIF检测的效果造成不良影响。因此本研究的DIF值的变化范围设置为0.24～0.64。从研究结果来看，样本量和DIF值确实影响SIBTEST方法的检测效果，并且样本量和DIF值对SIBTEST方法的检测效果的影响存在交互作用。由于本研究所选用的SIBTEST检测软件本身的限制，该软件能检测的最大样本量是7000，如果想要检测更大样本量的数据，则需要对SIBTEST软件进行拓展。从本研究的研究结果来看，当样本量达到5000～7000时，DIF值为中等偏大时SIBTEST方法的检测效果就不太稳健了。可以想象，如果样本量增大到2万或者更大，那么可能DIF值为中等大小时SIBTEST方法的I型错误就不再满足稳健的标准。当样本量很大的时候，在用SIBTEST方法来检测DIF前就很有必要采取一些必要的措施，例如对样本进行随机抽样达到降低样本量的目的，或者在检测时采用效应值来对抗虚假的统计显著性。

6 研究结论

（1）在一定的DIF值和样本量条件下，SIBTEST方法的检验力和I型错误随着样本量和DIF值的增大而增大。样本量和DIF值太小，会导致SIBTEST方法的检验力不充分。样本量和DIF值过大，不仅对检验力的提高没有帮助，反而会使I型错误急剧增大。

（2）当用SIBTEST方法对实测数据进行DIF检测时，1000～2000的样本量是比较合适的。

（3）当用模拟数据进行SIBTEST方法的模拟研究时，如果选用的DIF值较小时（0.24～0.32），那么样本量不能少于2000；如果选用的DIF值为中等大小时（0.40～0.56），那么样本量不能少于1000；如果选用的DIF值为较大时（0.64），那么样本量不能少于500。

[1]董圣鸿，马世晔.三种常用DIF检测方法的比较研究[J].心理学探新，2001（1）.

[2]李付鹏.能力水平分组对Mantel-Haenszel方法检验DIF效应的影响分析[J].中国考试，2011（9）.影响分析[J].中国考试，2011（9）.

[3]Shealy，R.，Stout，W.A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DIF as well as item bias/DIF.Psychometrika，1993，58：159-194.

[4]Clauser，B.E.，&Mazor，K.M.Using statistical procedures to identify differential item functioning test items.Educational Measurement:Issuesand Practice，1998，17：31-44.

[5]William Stout，Louis Roussos.SIBTESTManual，1996.

[6]Cohen，J.Statistical power analysis for the behavioral sciences.Hillsdale，NJ:Erlbaum.1988，2nd ed.

[7]Bradley，J.V.Robustness?The British Journal of Mathematical&Statistical Psychology，1978，31：144-152.