模块化科目考试的分数转换——以香港中学文凭考试为例
温忠麟 罗冠中
试卷中的模块是指一组题目,模块化科目的试卷含有多个模块,其中有一个模块是该科考生必答的,另有若干模块,由学生自行选答。不论是必考科目还是选考科目,都可以设计模块化试卷,成为模块化科目。2012年开始的香港中学文凭考试(HKDSE)①2012年之前,香港的学制和英国的一样,中学5年,预科2年,大学本科3年。2012年开始改为和内地学制一样,即初中3年,高中3年,大学本科4年。之前的会考和高考则合并成一次考试“中学文凭考试”。,许多科目都是模块化科目。例如,英语是必考科目,有4个分卷(阅读、写作、聆听和口语),其中阅读和聆听都是模块化设计。以阅读为例,其中有一个模块是必答的,另有两个模块让考生选择其中一个。两个选答模块中,一个模块比较容易,另一个模块则比较难。显然,这样的模块化设计是不能使用原始分的,一定要解决模块之间的分数等值转换问题。又如,资讯与通讯科技是选考科目,有4个选答模块。虽然事先不知道哪个模块比较难,但可以肯定的是难易程度不会是相同的,除非碰巧。所以,只要有模块化科目或者模块化分卷设计,就需要等值转换。
因为模块化科目有一个模块是必答的,所以等值转换的思路是以必答模块为“桥梁”,实现选答模块的等值,相应的等值设计为通常教科书上说的铆测验—非等组设计(漆书青,戴海崎,丁树良,2002),其中必答模块题目为铆题。相对于整份试卷,每个模块的题目往往较少(甚至只有一个题目),并且是在原始分数处理的早期阶段,所以模块之间的分数通常都不会使用项目反应理论(IRT)进行等值。一种常规方法是等百分位等值(equipercentile;漆书青等,2002)。和其他等值方法一样,等百分位等值也需要假设不同模块都是测试相同的能力。
等百分位等值原理容易理解,简单说就是,比较同一组考生在模块A和模块B的表现,将两个模块中百分等级(percentage rank)相同的分数作为是等值的,这样就实现了模块A和模块B的分数等值。例如,同一组考生在模块A中分数低于25的有40%,在模块B中分数低于30的有40%,则认为模块A的25分与模块B的30分等值。
对于等百分位等值,无论是从统计原理的描述还是对原理的理解都没有多少问题,问题在于针对具体考试中不同的设计,如何实现等值的具体计算。本文以香港中学文凭考试为例,介绍不同设计情况下模块之间的实际等值转换方法,但首先要介绍如何实现等百分位等值的计算。
1 两个模块的等百分位等值转换计算方法
在考虑将两个模块分数等值时,所谓的考生是指同时参加了两个模块考试的考生。下面是等百分位等值的具体步骤,可以实现模块A分数到模块B分数的等值转换:
第1步:频数分析
分别对模块A和模块B做频数分析,得到频数表:
(1)将考生按分数由低到高(升序)排队;
(2)对每个可能的分数(0分到满分),计算得到该分数的考生人数;
(3)对每个可能的分数,计算低于该分数的考生人数。
第2步:计算每个考生的百分等级
分别对模块A和模块B计算每个考生的百分等级。如果有多个考生获得相同的分数,如何计算比其分数低的考生人数呢?如果理解为严格低于该分数的考生人数百分比,可以想到,有时候分数变化一分,百分等级会激烈变化。比较合理的做法是,将同样分数的考生,视为有一半人低于该分数,另一半人则高于该分数。这样,一个给定分数x的百分等级为:

其中B为低于分数x的考生人数,E为等于分数x的考生人数,N为所有考生人数。
第3步:建立模块A到模块B的分数转换公式
为了容易区分,将模块A的分数x的百分等级记为PrA(x),模块B的分数y的百分等级记为PrB(y)。通常,模块A的一个分数x(百分等级为PrA(x),在模块B中未必刚好有现成的一个分数y,其百分等级PrA(y)与PrA(x)正好相等。但我们可以在模块B中找到两个相邻的分数y1和y2(其中y1<y2),使得相应的百分等级满足PrB(y1)≤PrA(x)<PrB(y2),然后用线性插值方法计算与x对应的等值分数f(x)。计算y1、y2和线性插值公式如下:
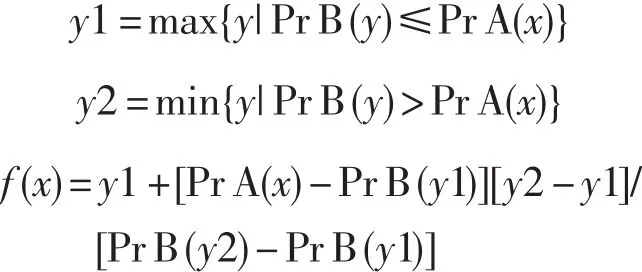
y=f(x)就是模块A的分数x在模块B中的等值分数。显然,当PrB(y1)=PrA(x),f(x)=y1。一些特殊点的转换如下:
(1)f(0)=0;
(2)如果PrA(x)<PrB(0),则f(x)=0;
(3)如果PrA(x)≥PrB(full_B),则f(x)=full_B,其中full_B是模块B的满分值。
第4步:将模块A的每个分数转换到模块B的等值分数
使用上面建立的公式y=f(x),就可以将模块A的每个分数,都转换到模块B中的一个分数,转换后的分数四舍五入后,称为模块B等值分数,以区别于模块B分数。
通过上述步骤,就可以实现一个模块到另一个模块的分数等值转换,这是模块化试卷等值转换的基础。
需要注意的是,零分考生通常只是写个名字什么都不做,反映不了真实能力。如果零分考生不是偶然的一两个,应当先将所有零分考生剔除后再进行等值转换。
2 普通选答模块的分数转换
一般的模块化试卷,两个或多个选答模块处于平等地位,事先不会有意地让某个模块更难或者更易,而是尽可能使不同选答模块的难度相当,这样的选答模块称为普通选答模块,简称为选答模块。例如,香港中学文凭考试选考科目中,“企业、会计与财务概论”有2个选答模块,必答模块占40%,选答模块占60%。“资讯与通讯科技”有4个选答模块,必答模块占55%,选答模块占25%,校本评核占20%。“设计与应用科技”是5个选答模块任选其中2个,必答模块占30%,选答模块占30%,校本评核占40%。这种选答模块进行等百分位等值时,不宜采用通常教科书中的“链等百分位等值”。
所谓链等百分位等值(漆书青等,2002),是将选答模块甲分数等值到必答模块分数(用模块甲考生数据),再将必答模块分数等值到选答模块乙分数(用模块乙考生数据),实现模块甲与模块乙的等值。这种链等百分位等值的缺点是模块甲考生分数需要经过两次转换才能转换到模块乙等值分数,而模块乙考生分数是原来的分数,这样两个模块就不平等。如所知,分数转换其实是一种估计,会有估计误差,两次转换的估计误差还可能会累积。
比较公平的做法是,将每个选答模块分数都转换到必答模块等值分数,做法是将选答模块视为模块A,将必答模块视为模块B,使用同时参加了选答模块和必答模块的考生数据,按上一节的步骤,就可以实现选答模块到必答模块的分数转换。这样做,每个选答模块的分数都转换了一次,然后按预设的权重(必答模块和选答模块权重)计算全卷分数。
3 包含难易选答模块的分数转换
出于特殊的考虑,有的科目可能会有难易不同的选答模块,并且命题的时候就明确了哪个模块易、哪个模块难。例如,香港中学文凭考试的英语,阅读分卷和聆听分卷都有三个模块:必答模块、易模块和难模块。这时,如果还是将易模块和难模块分数都等值转换到必答模块,对于易模块而言,问题不大,但对于难模块,转换的时候就会出现所谓的“天花板效应”,即在难模块排名靠前的许多考生分数,转换到必答模块后都变成了(必答模块的)满分或接近满分,这部分考生在难模块上的不同表现难于区分,设置难模块失去了意义。
较好的做法是,采用链等百分位等值,将易模块分数转换到必答模块等值分数(用易模块考生数据),再将必答模块分数转换到难模块等值分数(用难模块考生数据)。最后,每个考生都有一个必答模块分数和一个难模块分数(或者等值分数),将两种分数按预设的权重(必答模块权重和难模块权重)计算全卷分数。具体步骤如下:
第1步:将易模块的每个分数转换为必答模块等值分数
将易模块作为模块A,必答模块作为模块B,利用同时参加了这两个模块的考生数据,按第一节中的步骤,就可以将每个易模块分数,转换为必答模块等值分数。为了减少误差,转换后的分数暂时不要四舍五入。
第2步:将必答模块的每个分数转换为难模块等值分数
将必答模块作为模块A,难模块作为模块B,利用同时参加了这两个模块的考生数据,按第一节中的步骤,就可以将每个必答模块分数,转换为难模块等值分数。为了减少误差,转换后的分数暂时不要四舍五入。
第3步:将易模块的每个分数转换为难模块等值分数
根据第1步结果,对于易模块的每个分数Ei,都有一个必答模块等值分数Equa_Ei(带有小数),可以找到必答模块的两个相邻分数Ci1和Ci2,使得Ci1≤Equa_Ei<Ci2。而根据第2步结果,必答模块分数Ci1和Ci2在难模块有相应的等值分数,分别记为Equa_Ci1和Equa_Ci2。用线性插值方法,易模块分数转换为难模块等值分数的公式为:
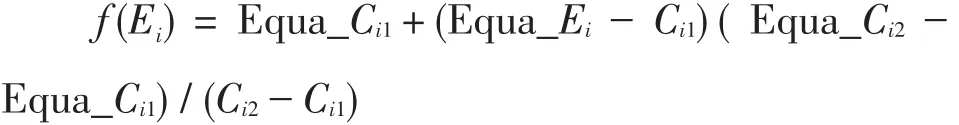
显然,当Equa_Ei=Ci1时,f(Ei)=Equa_Ci1。如果Equa_Ei超过了必答模块的满分值,则f(Ei)等于必答模块满分值对应的难模块等值分数。
和前面说过的一样,链等百分位等值使得易模块分数被转换了两次,误差会累积,但为了将高能力考生区分出来,避免“天花板效应”,将易模块分数转换到难模块等值分数是比较好的做法。此外,易模块排名靠后的一些考生分数,转换到难模块等值分数后都变成了(难模块的)零分或接近零分,出现所谓的“地板效应”,这部分考生在易模块上的不同表现难以区分。不过,根据“两害相权取其轻”的原则,情愿出现“地板效应”也要避免“天花板效应”,因为高考的作用是选拔人才,很有必要区分能力高端的学生,而没有太多必要区分能力低端的考生,无论用什么方法转换分数,这部分考生都会落榜。
说明一下,香港中学文凭考试的每一科,都会按考生分数评级,包括1~5级,其中5级中排名最靠前的10%评级为5**,接下来的30%评级为5*,剩下的60%评级就是5。还有一个规则是,选答易模块的考生,在该分卷最高只能达到4级。这些都是考试设计的政策规定。
4 全科—半科分数转换
香港中学文凭考试的选考科目中,不仅有物理、化学和生物这些人们熟悉的科目,还有一个特殊的科目,叫做组合科学(Combined Science),考生可以选择物理、化学和生物三科中的任何两科,其中的任何一科只是组合科学这个科目的半科,考试范围占了全科的一半左右,即组合科学是由两个半科组成。半科的题目大多数来自全科,这些题目就成了全科(如物理)和相应半科(如组合科学中的半科物理)的共同题,简称为全科—半科共同题。
这种全科—半科设计,还是使用等百分位等值方法进行分数转换。不过,单单用半科考生的数据是不够的,需要用到全科考生的数据。以物理全科—半科为例说明分数转换的步骤。第一步是使用物理半科考生数据,将半科分数转换到共同题分数;第二步是使用物理全科考生数据,将共同题分数转换到全科分数。这样,就将半科分数转换到全科分数了。
不过,因为香港中学文凭考试最后是看等级,所以关键是如何根据物理全科的等级切分点(cut point,即每个级别的最低分数),去确定物理半科的等级切分点。这样,转换分数的问题,变成转换切分点的问题。但转换过程与上面说的刚好相反,因为转换分数是要将每个半科分数转换到一个全科分数,而转换切分点却是要将每个全科切分点转换到一个半科切分点。思路是,先将全科切分点转换到共同题切分点,再将共同题切分点转换到半科切分点。步骤如下:
第1步:得到全科的等级切分点
首先要得到全科(即物理、化学和生物)分数1~5级的切分点。如何得到全科的等级切分点是与模块化科目等值不同的问题,需要从香港中学文凭考试必考科目中文、英语、数学和通识的等级入手,这里不拟涉及。
第2步:将全科切分点转换到全科—半科共同题切分点
使用全科考生数据,将全科切分点转换到全科—半科共同题切分点。这个过程类似于将模块A的一个分数转换到模块B等值分数。
第3步:全科—半科共同题切分点转换到半科切分点
使用半科考生数据,将全科—半科共同题切分点转换到半科切分点。这个过程也类似于将模块A的一个分数转换到模块B等值分数。
第4步:得到组合科学切分点
对于某个等级(如3级),将两个半科的切分点相加,就是该等级的切分点。例如,假设物理半科的3级切分点是70,而化学半科3级切分点是60,则综合科目(物理和化学)的3级切分点是130。
5 讨论
大陆从2004年开始启动的高中新课程改革,让学生从高二起,可以根据自己的爱好和能力倾向选择适合自己的选修课程。本来,作为改革的配套措施,高考科目的模块化可以说呼之欲出。然而,由于还使用原始分数,使得高考模块化科目难以推行。有的科目试卷有少量选答题,在没有分数等值转换的情况下,只能根据经验,在命题的时候尽量使得各选答题的难度相当。但经验有时候是不靠谱的,有模块化设计的科目,应当有配套的分数等值转换方法。
无论什么等值方法,都有其前提假设、适用范围和缺点。没有一种方法绝对比另一种方法好,需要根据具体的考试科目设计,选择缺点较小、操作可行、较易为持分者理解和接受的方法。
理论上说,如果两个模块的分数分布都服从正态分布,则等百分位等值就成了线性等值。其实,只要两个模块的分数分布完全相同,等百分位等值就是线性等值。但在实践中,两个模块的分数分布很难一模一样,也不会刚好是正态分布,有些分数上的频数明显偏多或偏少,结果是百分等级不是随着分数的增加而逐渐上升,而是时快时慢。我们将同样分数的考生,视为一半低于该分数、一半高于该分数,在一定程度上减轻了百分等级波动幅度。
如果是通过样本考生分数建立等值转换关系,但需要对总体考生分数进行等值转换,等百分位等值也可能有问题,因为样本考生分数范围可能比总体考生分数范围窄,因而总体考生的低分段或者高分段,可能无法确定等值关系。不过,我们不是抽样建立等值转换关系,而是使用全体考生分数,除了个别缺考情况外,用来建立等值转换关系的考生就是需要转换分数的考生,即总体和样本是相同的。在香港中学文凭考试英语科有难易模块设计时,用到了链等百分位等值,在建立必答模块到难模块的等值转换时,用的是难模块考生数据,而需要使用该等值转换关系的却是易模块考生,所以可能出现低分段分数无法区分的情况,即“地板效应”,这是为了避免“天花板效应”作出的牺牲。
无论是为了减轻百分等级波动幅度,还是为了使转换关系在低分段或者高分段不会突然失效,都可以预先对频数分布做光滑化(smoothing)处理(Livingston,2004),然后才计算百分等级。这样可以保证等值关系是一条光滑上升的曲线。
[1]Livingston,S.A.Equating Test Scores(Without IRT).Princeton,NJ:Educational Testing Service.2004.
[2]漆书青,戴海崎,丁树良.现代教育与心理测量学原理[M].北京:高等教育出版社.2002:201-214.

