线性代数课堂教学初探

王敬童

(湖南商学院信息学院，湖南长沙410205)

线性代数课堂教学初探

王敬童

(湖南商学院信息学院，湖南长沙410205)

针对线性代数课程的自身特点，结合教学实践，从概念教学、命题教学、解题教学等几个方面，对线性代数课堂教学进行了初步探讨。

线性代数;概念教学;命题教学;解题教学

线性代数是讨论代数学中线性关系经典理论的课程，是高等院校理工类、经管类等各专业的一门重要的基础理论课，它对于培养学生的计算能力、抽象思维能力、逻辑推理能力和工程实践能力有着不可忽视的作用。由于线性代数内容抽象、形式化程度高，而且教材中理论多、应用少，学生在学习这门课程时普遍感到有一定的难度。本文根据线性代数课程的特点，并结合笔者多年的教学实践经验，从概念教学、命题教学、解题教学等几个方面，对线性代数课堂教学进行研究和探讨。

一 概念教学

概念是思维的细胞，是浓缩的知识点。在基本概念的教学中，教师如果能巧妙地引入重要概念，就会淡化数学概念的高度抽象性，充分激发学生的学习兴趣和创造热情。课堂教学中，应充分展现概念的发生发展过程——展示概念的发生和发展的实际背景，引导学生充分运用已有的知识结构弄清概念的来龙去脉，认识概念的本质属性，明确和理解概念的内涵与外延，从而构建起相应的概念。在概念教学实践中，可以通过类比、联想概念之间的异同，找出每个概念的特点，以挖掘出每个概念的关键点。

如n阶行列式概念的引入。在现行的大多数线性代数教材中，行列式是学生接触的第一个概念，也是非常抽象的一个概念。在教学中，我们一般由初等数学中常见的二(三)元线性方程组的简洁公式解入手引入二(三)阶行列式。对于含有n个方程n个未知量的线性方程组:

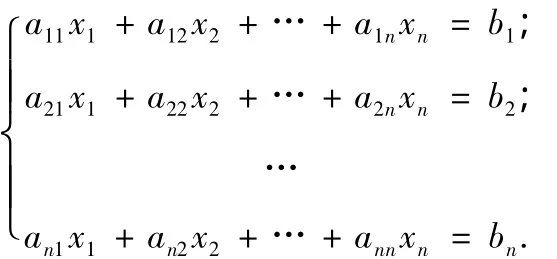
这类方程总可以用消元法来求解，但是消元法没有一个统一的公式，而解的统一公式在很多情况下有很重要的意义(就像一元二次方程公式解的作用)，因而有必要寻求该类线性方程组的公式解。我们一般会考虑，通过定义一般的n阶行列式，来给出它的公式解，进而引导学生，不难发现:二(三)阶行列式有如下共同特征:(1)二阶是2!=2项的代数和，三阶是3!=6项的代数和;(2)它们的每一项都是不同行不同列元素的乘积，并且包含了所有可能的不同行不同列元素的乘积。除符号外，二阶的项可写成:a1j1a2j2，三阶的项可写成:a1j1a2j2a3j3。这样学生就不难发现，从二(三)阶行列式推广至n阶行列式唯一的障碍就是乘积项的符号，从而顺理成章地引入排列及逆序数等概念，进而通过逆序数归纳定义n阶行列式。在教学中，还可以进一步引导学生从二(三)阶行列式及其展开式的结构入手探寻其共同规律，通过引入余子式和代数余子式的概念，进而导出用低阶行列式定义高一阶行列式的思想，即从行列展开的角度定义n阶行列式。这是现行线性代数教材中常用的2种n阶行列式的定义，它们在不同情况下有不同的作用。这样，学生通过自己循序渐进的探究，极大地激发了探求新知识的欲望，同时也为Cramer法则以及矩阵的引入做好了铺垫。

再如矩阵运算的引入。矩阵理论是线性代数的核心内容之一，而矩阵的运算是矩阵理论的主动脉。所以如何巧妙地引入矩阵的运算是非常关键的。在教学中，为加深学生对矩阵运算性质的理解，可引导学生将矩阵与数的运算性质作类比。例如定义了矩阵的加法、减法与乘法之后，学生理所当然地就会思考能不能像数的运算那样定义矩阵的除法运算呢?即这样定义呢?在肯定学生类比意识的同时，我们可以与学生一起探究，在数的运算中，除法可以看成是乘法的逆运算，b÷a=，因为数的乘法满足交换律，因此有确切的含义。但在矩阵运算中，因为乘法不满足交换律，BA－1=A－1B往往不成立，因而B÷A=没有确切的含义，因此不能定义矩阵的除法。进一步指出，数的运算里边，通过倒数的引入实现了除法通过乘法来实现，可以把这种通过倒数来实施除法的思想延拓到矩阵中来。若记b=a－1，则数的倒数由ab=ba=1唯一确定，而矩阵乘法中单位矩阵E相当于数的乘法运算中的1，从而水到渠成地引入逆矩阵的概念，进一步指出，可逆矩阵是一类最重要的矩阵，应用非常广泛，如Cramer的证明、求解矩阵方程等。在教学中，将要学习的知识与学生以前掌握的知识联系起来再深入讲解，这样，一方面使陌生的、抽象的、晦涩难懂的知识在学生心中建立起熟悉、亲切、能学易学的形象;另一方面，可激发学生的知识创造力。

又如线性相关概念的引入。线性相关概念是线性代数课程的一个难点，又是重点，对它的理解如何将直接决定着对该课程中心内容的掌握及应用的程度，这个概念是提升学生数学能力的一个很好凭借。而线性相关性概念的抽象性使得学生对这些概念缺乏感性认识，难以把握概念的本质。因而简短而频繁地返回主题能更好地帮助学生深刻理解，所以在教学内容安排上可以交叉重叠，层层推进。在教学中，可结合二维与三维向量线性相关性的几何直观加深理解，其效果较直接给出定义要好。

二 命题教学

在课堂教学中，应充分展现命题的探究过程——通过实际问题或数学问题的情景展示，使学生在实验观察、主动探索和讨论中获得关于命题的直觉认识，并形成关于命题的猜想，感受命题的发展演变和形成的过程。问题的设计是学生理解和接受新概念的关键点，以及学生学习新内容的兴奋点，从而能达到引发学生思考，引导学生提问题，进一步促使学生很自然地得出并理解结论的目的。

如讲解初等矩阵与初等变换的关系时，可举例用三类初等矩阵左乘与右乘矩阵，引导学生通过观察结果总结出定理的内容。

再如在讲解矩阵乘法的三大特征时，可举例:

容易算得:

如矩阵的秩是矩阵的一个非常重要的不变量，是讨论向量组的线性相关性、深入研究线性方程组等问题的重要工具。学习了其基本性质，以及用初等变换求具体矩阵的秩之后，结合n阶矩阵A可逆的充分必要条件是A可以表示为若干初等矩阵的乘积，引导学生从初等变换的角度去看待可逆矩阵左(右)乘矩阵，不难发现下面的重要性质:

设P、Q为满秩矩阵，则r(A)=r(PA)=r(AQ)=r(PAQ)。

课堂中让学生思考:

三 解题教学

在线性代数的学习中，学生普遍反应课听得懂，但解题却力不从心，没有一把解题的万能钥匙。这是因为学生还不习惯线性代数的高度抽象性，同时这方面的基本思维训练缺失。在教学中，教师应充分展现解题思路的获得过程——不仅要展示如何从题设、结论的等价条件出发，做出具体分析，如何联想、探索、猜想、推理、转化，如何挖掘易被忽视的语义信息及处于隐蔽状态下的已知条件的思维过程，还要展示在解题思路受阻时，如何合理变换策略，另辟蹊径，从而达到目的的思维过程。只有这样，才可以使数学结论生动、鲜活和充实，成为学生易于理解和接受的东西。也只有这样，才能使学生领会到数学的思想内涵，才能使学生的数学思维能力得到培养，才能使学生体会到数学发现和创造的乐趣，使学生感受到数学的美和内在魅力。如初等变换法求矩阵的逆。问题提出:《浅性代数》在第二章第三节中给出了矩阵A可逆的充要条件的同时，也给出了利用伴随矩阵求逆矩阵A－1的一种方法，即A－1=该方法称为伴随矩阵法。但当矩阵A的阶数较大时，求A* 很繁琐，此方法不实用，而分块思想只适应于某些特殊的高阶矩阵，不具普遍性。那么如何找到一种简单的方法呢?由矩阵的分块乘法有:

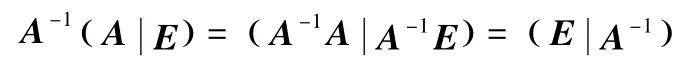
可以发现:n阶矩阵A可逆的充分必要条件是A可以表示为若干初等矩阵的乘积。因此，由初等矩阵与初等变换的关系可知，求矩阵A的逆矩阵A－1时，可构造矩阵n×2n矩阵(A E)，然后对其施以初等行变换将矩阵A化为单位矩阵E，则上述初等变换同时也将其中的单位矩阵E化为 A－1，即

这就是求逆矩阵的初等行变换法。当然也可以利用初等列变换，事实上

进一步引导学生:A行等价于其行最简形F，则存在可逆矩阵P，使得PA=F，如何求这个可逆矩阵P?(提示:(这个可逆矩阵P唯一吗?)随着问题的解决，学生不难发现初等行变换求逆矩阵是其一特殊情况。

进一步铺设问题:求逆矩阵的初等变换法能否求解矩阵方程AX=B、XA=B?

问题分析:其实推导求逆矩阵方法的过程就是求解矩阵方程的过程，因为求A－1就是求解矩阵方程AX=E的解，而对一般的矩阵方程AX=B只要将(A E)中的E换成B，然后利用初等行变换即可。事实上A－1(A B)=(E A－1B)即

这样就给出了用初等行变换求解矩阵方程AX=B的方法。

同理，求解矩阵方程XA=B，等价于计算矩阵BA－1，亦可利用初等列变换求矩阵BA－1．即?

在教学中，可让学生课后思考:①能用初等行变换求解矩阵方程XA=B吗?②能用初等变换求解矩阵方程AXB=C吗?

四 结 语

在大学数学教学中，线性代数教学有着非常重要的基础地位，课堂教学所涉及的细节太多，举凡纲要之本，则是课堂教学设计。教师应在钻研教材的同时，精心设计和组织教学内容，巧妙引入概念，有目的地设计聚合式的问题情景，充分展示知识的发生发展过程，挖掘其思想内涵，引导学生主动获取、发现问题，从有关的概念、定理及其证明的过程中寻找方法、挖掘本质、领悟思想，不仅要关注结果，更要关注过程，从而有效提高学生的综合数学素养。

［1］同济大学数学教研室．工程数学－－线性代数(第五版)［M］．北京:高等教育出版社，2007．

［2］北京大学数学系几何与代数教研室小组．高等代数(第三版)［M］．北京:高等教育出版社，2003．

［3］陈维新．线性代数(第二版)［M］．北京:科学出版社，2008．

［4］梁晓毅．线性代数—题型与方法［M］．西安:西安电子科技大学出版社，2003．

［5］张禾瑞，郝炳新．高等代数(第四版)［M］．北京:高等教育出版社，1999．

［6］赵慧斌．问题驱动是线性代数有效的教学法之一［J］．高等数学研究，2008(4)．

G642．0

A

1674－5884(2012)04－0085－03

2012－03－04

王敬童(1973－)，男，湖南双峰人，讲师，博士，主要从事代数学与信息安全研究。

(责任编校 晏小敏)