似曾相识揭本质 由此及彼促发展
——探求2类递推数列的通项公式
●
(余姚市第七中学 浙江余姚 315450)
似曾相识揭本质由此及彼促发展
——探求2类递推数列的通项公式
●吴建洪
(余姚市第七中学 浙江余姚 315450)
在众多的高三数学模拟试卷中,经常会碰到一些数列求通项an和前n项和Sn的试题.尽管这些试题的已知条件形式各异,但究其本质,最终都可归纳为最基本的递推数列求通项an和前n项和Sn的问题,如:
例1在数列{an}中,Sn为其前n项和,满足Sn=kan+n2-n(k∈R,n∈N*).若数列{an-2n-1}为公比不为1的等比数列,求数列{an}的通项与前n项和Sn.
例2已知数列{an}满足a1=5,a2=2an+1+2n-1(n≥2),求数列{an}的通项与前n项和Sn.
尽管学生对形如
(1)
(其中A,C,a1是非零常数,且A≠1)和
(2)
(其中A,B,C,a1是非零常数)的基本递推数列求通项问题掌握得比较扎实,但由于对问题的本质不是很清楚,使得当学生碰到形如
(3)
(其中A,B,C,a1是非零常数,且A≠1)和
(4)
(其中A,B,C,D,a1是非零常数)等情形时(注意到:式(3)与式(1)相似,式(4)与式(2)相似),常常会感到束手无策,难以为继.
事实上,递推数列求通项问题,一般情况下只需将不同形式的数列递推关系式,运用化归思想,转化为特殊的等差数列或等比数列进行求解即可.若能清楚地知道这一本质特征,再加上一定的变式技巧,不仅能很快地解决一般递推数列求通项的问题,而且对培养学生分析问题与解决问题的能力有较大帮助.本文将围绕2种类型的递推数列问题展开探讨.
类型1已知数列{an}满足
其中p,r,a1是非零常数,且p≠1,求通项公式an.
分析对于众多的递推数列问题,这是一种最基础、最重要的题型.熟练掌握本题最具本质的解法,可为其他递推数列问题的解决奠定坚实的基础.
当n≥2时,由待定系数法得

变式1已知数列{an}满足
其中p,r,a1是非零常数,求通项公式an.
分析变式1将类型1中的常数r变为rn,一种自然而朴素的想法是,将指数rn通过变形转化成常数.
方法1当n≥2时,等式an=pan-1+rn两边同除以rn,得
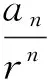
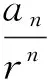

即转化为类型1.
当然,变式1还有一种更妙的解法.
方法2当n≥2时,等式an=pan-1+rn两边同除以pn,得

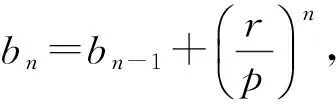
变式2已知数列{an}满足
其中p,r,q,a1是非零常数,求通项公式an.
分析对于递推关系式an=pan-1+rn+q,可先转化为等比数列

bn=pbn-1+rn,
即为变式1.
如例2,当n≥2时,由an=2an-1+2n-1得
an-1=2(an-1-1)+2n,
令bn=an-1,得
bn=2bn-1+2n,
即为变式1.进一步计算可得
an=(n+1)2n+1,
Sn=n·2n+1+n.
变式3已知数列{an}满足
其中A,B,C,a1是非零常数,且A≠1,求通项公式an.
分析变式3将类型1中的常数r变为关于n的一次式Bn+C,仿变式2,运用待定系数法将该一次式转化成常数.
当n≥2时,由an=Aan-1+Bn+C得
an+λn+μ=Aan-1+Bn+C+λn+μ=
Aan-1+(B+λ)(n-1)+C+μ-B-λ=

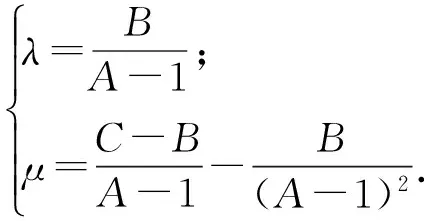
不妨设
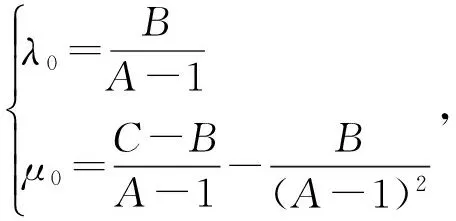
则当n≥2时,
an+λ0n+μ0=A[an-1+λ0(n-1)+μ0],
从而将数列{an}化归为以a1+λ0+μ0为首项,以A为公比的等比数列{a0+λ0n+μ0}.
变式4数列{an}满足
求通项公式an.
分析相邻3项间的递推数列问题比相邻2项间的递推数列问题麻烦,但只要抓住解决此类问题的本质,变式4的解决便水到渠成.为了叙述方便,变式4以人教版必修5“数列”复习参考题B组中的习题为例.
例3已知数列{an}满足a1=5,a2=2,an=2an-1+3an-2(n≥3),求数列{an}的通项公式.
(2)2005~2009年城市化与生态环境耦合协调度增长速率有所提高,表明城市化子系统和生态环境子系统进一步协调,协调类型逐步过渡为低水平协调阶段。这一时期的城市化综合水平持续增加,城市经济发展保持稳定速率,而这一时期的生态环境综合水平从2005年开始回升。通过查看各项指标情况可以发现,这一时期在环保等投资与GDP的比值,生活垃圾无害化处理率,人均公共绿地面积,工业固体废弃物综合利用率这部分生态环境响应指标的带动下,生态环境质量有较明显的改善,这些变化与湖南省的工作计划也密切相关,计划中提出发展循环经济,倡导生态文明,在发展中保护环境,实现速度与质量、效益的有机统一。
教参上的参考答案如下:
通过观察得
(5)
(6)
由式(5),式(6)得到2个等比数列

从而

分析从参考答案看,要求学生观察得出式(5)比较容易,但要求学生同时得到式(6)则有点困难.事实上,运用待定系数法,可以用以下2种方法求解.
方法1由an=2an-1+3an-2得
an+an-1=3(an-1+an-2).
令bn=an+1+an,则数列{bn}是以3为公比,以b1=a2+a1=7为首项的等比数列,从而
an+1+an=bn=7·3n-1,
即
an+1=-an+7·3n-1,
即转化为变式1.
方法2由an=2an-1+3an-2,运用待定系数法得
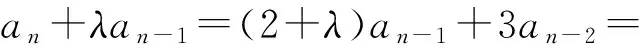

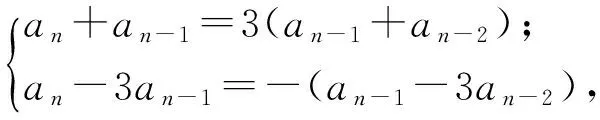
下与参考答案同.
解决数列问题不仅仅只是待定系数法的灵活运用,关键是运用化归的数学思想,将不具有规律的原数列递推关系式转化为具有特殊规律的递推关系式.因此,在日常教学过程中,教师应注重突出通性通法,渗透数学思想,理清思维的本原,抓住问题解决的本质,提高学生的数学能力.
类型2已知数列{an}满足
其中A,B,C,a1是非零常数,求通项公式an.
分析从形式上看类型2是一次分式结构,对于分式结构,一种行之有效的方法是取倒数.
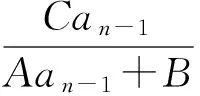
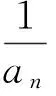



即转化为类型1.
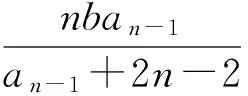
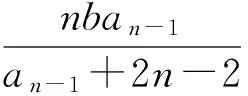

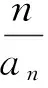
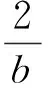
即为类型1.进一步计算可得
变式1若数列{an}满足Aan-Ban-1=Canan-1(n≥2),其中A,B,C是非零常数,求通项公式an.
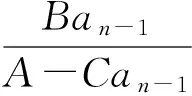

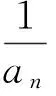

即转化为类型1.
变式2已知数列{an}满足
其中A,B,C,D,a1是非零常数,求通项公式an.
分析前面多次运用化归的数学思想,结合待定系数法顺利解决多种变式的递推数列求通项问题,对此变式仍可继续为之,以例5为例加以说明.
例5已知数列{an}满足
求通项公式an.

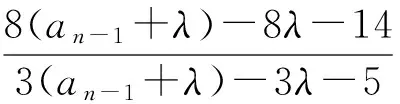
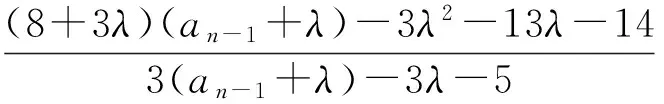
令 -3λ2-13λ-14=0,
(7)
得
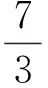
不妨取λ=-2,得
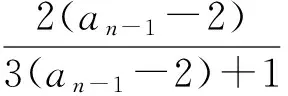
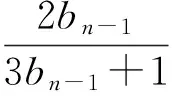

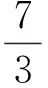
由于式(7)是关于λ的二次方程,相对于类型1,运用待定系数法求解相对复杂.但只要设计合理,还是可以顺利解决的.
数学问题的解决过程,其根本是从未知逐步向已知转化的过程,特别是对似曾相识的问题,往往需要透过表面研究本质,揭示规律,清楚推理,从而达到理想的教学效果.在教学过程中,教师应帮助学生真正理解和掌握数学基础知识和基本技能,合理运用数学思想,注重通性通法,这对于学生学好数学非常重要.

