一次、二次方程与不等式竞赛题赏析
●
(台州初级中学 浙江临海 317000)
一次、二次方程与不等式竞赛题赏析
●王飞兵
(台州初级中学 浙江临海 317000)
方程与不等式是数学学科的重要基础,它们内容丰富、形式灵活,具有很强的应用性.因此,以方程与不等式为载体的试题常常成为各种数学竞赛试题的考查热点之一.这些试题不仅考查了学生应该掌握的数学知识与解题技巧,更渗透了重要的数学思想,展示了学生的数学品质与素养.纵观近几年的各类数学竞赛题,方程与不等式类试题的考查重点已从知识点本身向知识点的应用方向发展.
1 一次方程或不等式(组)
1.1 一次方程(组)
例1母亲节到了,小红、小莉、小莹到花店买花送给自己的母亲.小红买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;小莉买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元;小莹买了上面3种花各2枝,则她应付______元.
(2010年全国初中数学联赛天津赛区初赛试题)
分析设玫瑰、康乃馨、百合花的单价分别为x元,y元,z元,根据已知条件,列出方程组

x+y+z=10,
因此小莹应付20元.
说明这是一个典型的一次不定方程应用题,消元与整体思想是解题的关键.
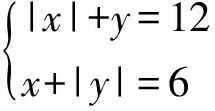
( )
A.1 B.2 C.3 D.4
(2007年《数学周报》杯全国初中数学联赛试题)

说明对于含绝对值的二元一次方程(组),依据绝对值的意义进行分类讨论是关键.
1.2 一次不等式(组)
例3已知关于x的不等式组
(1)
(2)
其整数解为1,2,3, 则整数对(a,b)的组数是
( )
A.32 B.35 C.40 D.48
(第21届希望杯全国数学邀请赛初中试题)
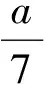

即

从而
0 得 a=1,2,3,4,5,6,7,b=16,17,18,19,20. 故整数对(a,b)可能的取值有35组. 说明本题求解的关键是对不等式组的整数解仅为1,2,3的全面理解,要熟练掌握不等式的基本性质,利用数轴研究不等式组的解会更直观. 1.3 一次方程与不等式(组)结合 例42位八年级同学和m位九年级同学一起参加象棋比赛,比赛为单循环,即所有参赛者彼此恰好比赛一场.记分规则是:每场比赛胜者得3分,负者得0分,平局各得1分.比赛结束后,所有同学的得分总和为130分,而且平局数不超过比赛局数的一半,则m的值为______. (2012年全国初中数学联赛试题) 分析设平局数为a,胜(负)局数为b,可得 2a+3b=130, 2a+2b=(m+1)(m+2), 于是 0≤b=130-(m+1)(m+2)≤43, 即 87≤(m+1)(m+2)≤130, 由此得 m=8或m=9. 说明本题整合了一次方程与不等式知识,具有一定的综合性与探究性. ( ). (2009年《数学周报》杯全国初中数学联赛试题) 分析当2a-b=0时,方程组无解;当2a-b≠0时,方程组的解为 由已知得 即 由a,b的实际意义为1,2,3,4,5,6,可得 共有5×2=10种情况; 或 共3种情况. 说明本题首先要理解二元一次方程组有无数多组解、无解、有唯一解的条件,再结合不等式组、概率相关知识解题. 2.1 一元二次方程 例6已知x1,x2是关于x的一元二次方程x2+(3a-1)x+2a2-1=0的2个实数根,使得(3x1-x2)(x1-3x2)=-80成立,求其实数a的可能值. (2011年全国初中数学联赛四川赛区试题) 分析由条件知 Δ=(3a-1)2-4(2a2-1)=a2-6a+5≥0, 解得 a≥5或a≤1. 又由根与系数的关系知 x1+x2=-(3a-1),x1x2=2a2-1, 于是 (3x1-x2)(x1-3x2)= 3(x1+x2)2-16x1x2= -5a2-18a+19. 由-5a2-18a+19=-80,解得 说明根的判别式与韦达定理是实系数一元二次方程的重要基础知识,也是解决有关方程根的性质、方程参变量的范围及代数式的值等问题的重要工具. 例7已知实数x,y,z满足x+y=4及xy=z2+4,求x+2y+3z的值. (2009年全国初中数学联赛预赛试题) 分析构造以x,y为根的一元二次方程t2-4t+z2+4=0,其中 Δ=16-4(z2+4)=-4z2≥0, 于是z=0,代入求得x=y=2,从而 x+2y+3z=6. 说明利用韦达定理构造以t为未知数的一元二次方程,再用判别式及解的意义求解. 例8边长为整数的直角三角形,若其2条直角边长是方程x2-(k+2)x+4k=0的2个根,求k的值并确定直角三角形3条边之长. (2010年全国初中数学联赛江西赛区初赛试题) 分析设直角边为a,b(a a+b=k+2,ab=4k. 因方程的根为整数,故其判别式为平方数,设 (k+2)2-16k=n2, 即(k-6+n)(k-6-n)=1×32=2×16=4×8. 因为 k-6+n>k-6-n, 所以 当k=15时, a+b=17,ab=60, 得 a=5,b=12,c=13; 当k=12时, a+b=14,ab=48, 得 a=6,b=8,c=10. 说明本题实际上是一个含参系数的一元二次方程的正整数根问题,这类题一般可用因式分解法将问题转化为二元一次方程组或二元一次不定方程求解,但要注意Δ为完全平方式. 2.2 可化为一元二次方程的问题 例9若方程x2-3x-1=0的2个根也是方程x4+ax2+bx+c=0的根,则a+b-2c的值为 ( ) A.-13 B.-9 C.6 D.0. (2010年全国初中数学联赛试题) 分析设m是方程x2-3x-1=0的一个根,则 m2-3m-1=0, 即 m2=3m+1. 由题意,m也是方程x4+ax2+bx+c=0的根,因此 m4+am2+bm+c=0, 把m2=3m+1代入此式,整理得 (9+a)m2+(6+b)m+c+1=0, 从而方程x2-3x-1=0的2个根也是方程 (9+a)x2+(6+b)m+c+1=0 的根.这2个方程实质上应该是同一个一元二次方程,从而 (9+a)x2+(6+b)x+c+1=k(x2-3x-1), 其中k为常数,故 即 b=-3a-33,c=-a-10, 因此 a+b-2c=-13. 说明本题通过降次将高次方程转化为一元二次方程,再根据同解方程根的意义解题. 例10整数a使得关于x,y的方程组 对于每一个实数b总有实数解,求整数a的值. (2008年全国初中数学联赛武汉市CASI杯选拔赛试题) 分析消去x,得关于y的方程 2y2+(3a-b)y-(b2-2a2+3b+4)=0. 根据题意得Δ≥0,即 (3b-a+4)2-(8a2-8a-16)≥0, 则 8a2-8a-16≤0, 即 8(a-2)(a+1)≤0, 得 -1≤a≤2, 从而整数a的值为-1,0,1,2. 说明本题通过消元将二元方程组转化为一元二次方程,再用方程根的判别式及不等式知识解题. 方程与不等式为解决数学问题(包括实际问题)提供了重要思想与方法,除了本文所讨论的常见试题类型外,还有分式方程、无理方程、应用题等其他类型的试题.方程与不等式类试题的解法没有固定的模式,需在熟练掌握各知识要点的基础上,根据试题本身的特点,灵活运用加以解决.
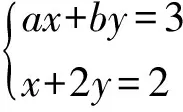

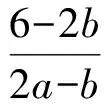

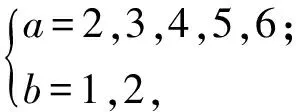
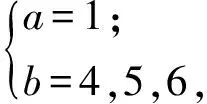
2 二次方程