巧用构造法证明不等式竞赛题

●

(东阳市外国语学校高中部 浙江东阳 322100)

巧用构造法证明不等式竞赛题

●厉军萍

(东阳市外国语学校高中部 浙江东阳 322100)

不等式的证明，凭借其简单的知识基础、独特的解题构思、发散的证明方向、奇妙的推理过程成为数学竞赛中永恒的热点之一.构造法，作为技巧性特别强的一种解题方法，主要通过构造适当的变量、等式、函数、图形、数列、模型等辅助手段，使问题转化，揭示出直观和本质的形式，从而有助于问题的解决.构造法与不等式证明的结合，往往能相得益彰，迸发出令人赞叹的思维火花.本文拟通过具体例子，分类阐述如何巧用构造法证明不等式竞赛题.

1 构造函数关系证明不等式

例1已知a,b,c∈(-2,1)，求证：abc>a+b+c-2.

分析此不等式2边关于a,b,c对称，且a,b,c都是一次的，可以尝试构造一次函数.

证明设f(x)=(bc-1)x-b-c+2，则

因为b,c∈(-2,1)，所以

故

从而

f(1)=bc-b-c+1=(1-b)(1-c)>0,

当x∈(-2,1)时，f(x)恒大于0，于是f(a)>0，即abc>a+b+c-2.

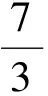
分析从条件和结论的形式看，a,b,c呈轮换对称，因此构造的函数也应当是轮换对称型.

证明由a2+b2+c2=(a+b+c)2-2(ab+bc+ca)=1-2(ab+bc+ca)，可知原不等式等价于

(1)

令f(x)=(x-a)(x-b)(x-c)=x3-x2+(ab+bc+ca)x-abc，则

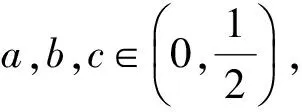
因此

整理即得式(1).故原不等式得证.

2 构造数列证明不等式

从数列的定义上看，数列可以看作一个定义在自然数集或其有限子集上的函数当自变量从小到大依次取值时的一系列函数值，因此可以从数列的角度理解函数或不等式.利用数列的通项公式和求和公式以及利用数列的特殊性质证明不等式，与一般证明相比较，常常显得新颖独特，别具一格.

(第19届莫斯科数学竞赛试题)

故原不等式成立.

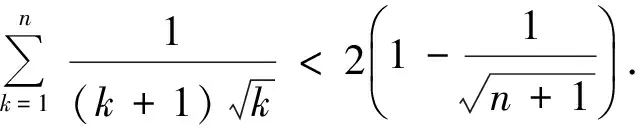
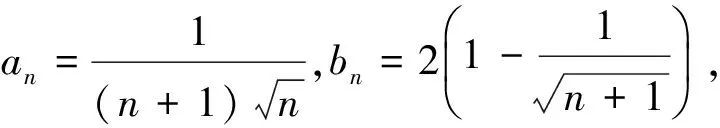
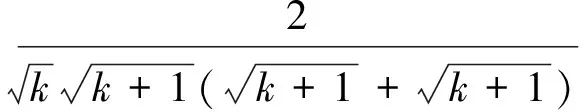
故

3 构造图形证明不等式

数形结合是最重要的数学思想之一，也是解决数学问题的有效方法之一.不等式的证明也是如此，如果问题条件中的数量关系有较为明显的几何意义或以某种方式可与几何图形建立联系，那么可以通过构造图形，将题设的条件及数量关系直接在图形中得到体现，然后在构造的图形中寻求所证的结论.

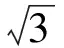
分析根据题意，本题的证明离不开三角形的知识，但怎样的三角形可以使解题更为方便，是首先应当思考的.

证明如图1所示，构造圆外切△ABC，使得3条边a,b,c满足a=y+z,b=z+x,c=x+y,则原不等式等价于

(2)

图1

(yz+zx+xy)2≥3xyz(x+y+z),

即证明

(yz)2+(zx)2+(xy)2≥xyz(x+y+z)，

而此式显然成立，故原不等式成立.

例6设x,y,z>0，求证：

分析三角形是最基本的平面图形，三角形中存在许多结论，如三角形的边角不等关系、正余弦定理和面积计算公式等是最基本的解题工具，巧妙利用这些知识解题往往能收到事半功倍的效果.

图2

证明如图2所示，∠APB=∠BPC=∠CPA=120°,设PA=x,PB=y,PC=z,则P为△ABC的费马点.易知

在△APB,△BPC,△CPA中，由三角形两边之和大于第三边，并将所得的3个式子相加，即得左边的不等式.

另一方面，在△ABC中，由例5的结论

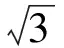
可得

(3)

从而

(4)

又ab+bc+ca≤a2+b2+c2，由式(4)可得

式(3)+式(5)×2得

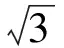
故

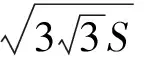
4 构造分布列证明不等式竞赛题

若随机变量ξ的分布列如表1所示，则方差

Dξ=P1(x1-Eξ)2+p2(x2-Eξ)2+…+pn(xn-Eξ)2+…=Eξ2-(Eξ)2≥0.

通过构造随机变量的概率分布列，可以证明一类不等式竞赛题.

例7如果正数x1,x2,…,xn的和为1，证明：

(第24届全苏数学竞赛试题)

分析构造分布列证明的关键在于构造适当的随机变量及其概率.本题可以用多种不同方法证明.

证明构造随机变量ξ的分布列如表2所示.

表2 随机变量ξ的分布列

则

由Eξ2-(Eξ)2≥0得

例8设a,b,c,d>0，且ab+bc+cd+da=1，求证：

(第31届IMO备选试题)

分析本题的证明关键仍然是如何根据题给条件和所证结论构造适当的随机变量及其概率.

证明构造随机变量ξ的分布列如表3所示.

表3 随机变量ξ的分布列

其中m=2(ab+bc+cd+da+ac+bd),则

由Eξ2-(Eξ)2≥0得

5 构造代换模型证明不等式竞赛题

代换法是证明不等式的常用方法，通过代换往往能将一个复杂的不等式转化为一个简单的或可直接运用公式证明的不等式问题.代换的方法很多，如均值代换、三角代换、线性代换、分母代换等，如何寻找一种合适的模型进行代换是解决问题的关键.

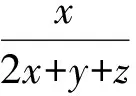
分析对于一类齐次型的分式不等式，可以通过分母代换，将原不等式转化为基本不等式证明问题.

证明令a=2x+y+z,b=x+2y+z，c=x+y+2z,则

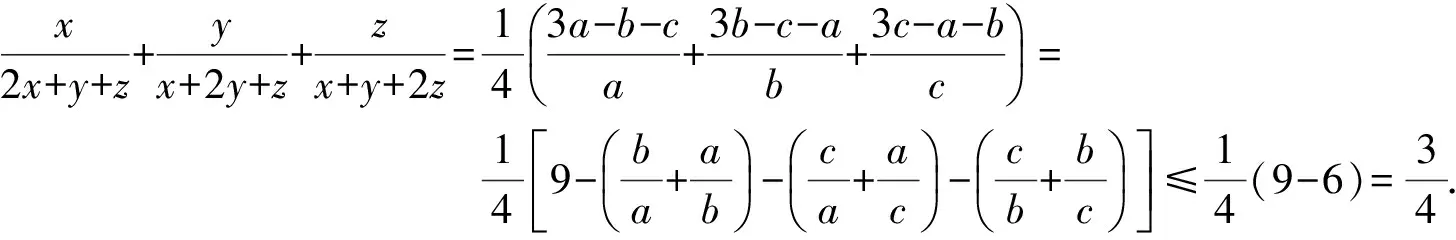
例10设x,y,z是大于-1的实数,证明:

(2004年IMO中国国家队培训试题)

分析本题x,y,z呈轮换对称形式，但每一个分式都不是齐次型，因此，先通过基本不等式将分式化为齐次型(含常数)是证明的第一步.

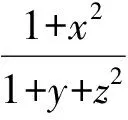
设p=2c+b,q=2a+c，r=2b+a,则

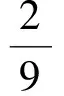
故原不等式得证.