六面体单元预应力钢束等效刚度计算研究

王晓宁 王维民

(中交第二公路勘察设计研究院有限公司，湖北 武汉 430056)

对于具有复杂形状的桥梁，用体单元进行有限元分析具有得天独厚的优势。在应用有限元进行结构分析时，预应力孔道和钢束对体单元刚度的影响一般不予考虑或通过经验得出，这必然会造成计算上的误差。本文从有限元方法的基本原理入手，推导得到体单元的等效刚度的计算方法，该方法可以适应各种不同形状的预应力钢束，经过算例检验，该方法具有较高的精度。

1 混凝土和钢束共同作用下单元刚度矩阵的计算

在应用有限元进行结构分析时，预应力孔道和钢束对体单元刚度的影响一般不予考虑，这样就造成单元的计算刚度小于单元实际刚度。混凝土构件在总体上是比较规则的，划分为混凝土单元后，在单元各边上的应力应变变化是比较均匀的，故可选用8结点六面体单元等参数单元，来计算考虑预应力钢束刚度影响的单元等效刚度。

1.1 基本单元特性

8结点等参数单元是一个直棱六面体，如图1所示。在参考坐标系下，这个六面体被变换为边长为2的正方体，参考坐标系ξηζ的原点位于它的形心处。

图1 等参变换示意图

以下是坐标变换模式和位移模式:

其中，n为结点个数，n=8时，是8结点等参数单元，它的形函数是:

其中，ξi，ηi，ζ为结点i的局部坐标，对于角结点它们分别为1或 －1，即:

在上式中，右端的三项均是距离为2的平面方程。

1.2 考虑预应力孔道和钢束的单元(计算单元)刚度矩阵计算

1.2.1 单元特性分析

现在我们考虑在一个正六面体单元中间取出一个预应力孔道后的新单元的计算方法。对于单元刚度矩阵[K]e=∫V[B]T[D][B]dV，定义V1，V2和V3代表的体积如图2所示。

图2 含孔道的六面体单元

则单元刚度矩阵(扣除预应力孔道后)可表示为:

现在令:

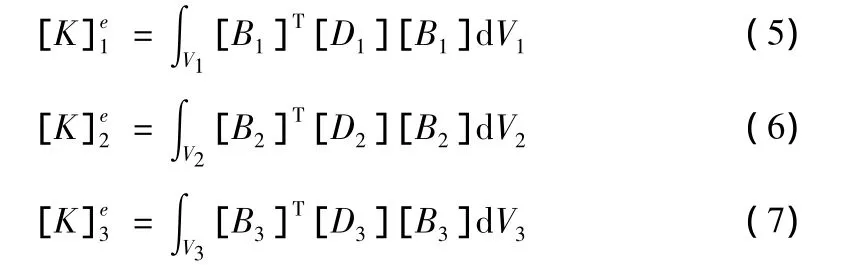
其中，V1，V2，V3均为部分相对于 V1的刚度矩阵;B1，B2，B3为各部分的几何矩阵;D1，D2，D3为各部分的弹性矩阵。

求得新的单元刚度矩阵为:

用这种方法就可以计算出包含预应力钢束的六面体单元的单元刚度矩阵。

1.2.2 V2，V3部分单元刚度矩阵

由于钢束材料具有均质，各向同性的特点，通常情况下其断面面积又是一定的，对其单元刚度的计算可以适当简化。

令μ∈[0，1]为孔道中心线上一点的弧长参数，有:

应用高斯积分进行积分(这里用2点高斯积分)。

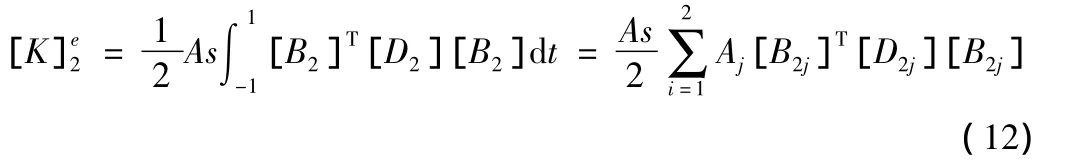
通过计算机方法可用上式计算出单元的刚度矩阵。

同理可以计算出预应力钢束部分的单元刚度矩阵，只是断面面积A和弹性矩阵[D]不同，这里不再赘述。

2 计算方法的应用与验证

2.1 实例

现在用一简单的预应力悬臂梁具体实现这一计算方法，见图3。

图3 悬臂梁单元划分示意图

xoy平面为固定端约束，尺寸为300 mm×600 mm×4 000 mm。经过多次试验，确定将悬臂梁划分为100 mm×100 mm×100 mm的正方体单元。根据上节计算公式可通过计算机方法计算出悬臂梁所有结点在各个方向上的位移。由于建立有限元模型是为了计算预应力钢束对混凝土单元刚度的影响，所以在计算过程中没有考虑结构自重和预加应力产生的挠度。在《桥规》里，用式(13)计算非开裂截面受弯构件在正常使用极限状态下的挠度:

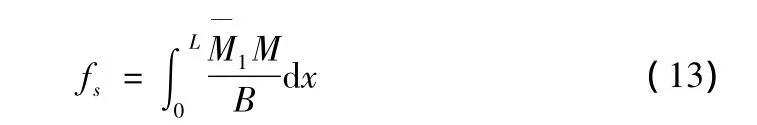
用图乘法得到计算构件任意截面处的挠度为:

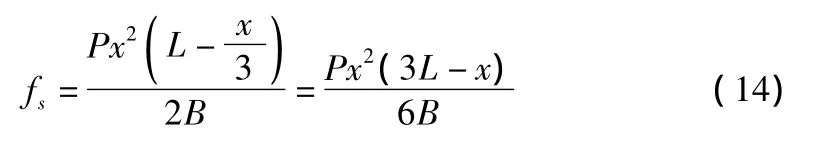
由此，可以计算出悬臂梁任意截面处的挠度。

2.2 计算结果和结论

1)两种方法的比较。

为了检验计算方法的正确性，把用有限元程序的计算方法与《桥规》的计算方法进行一下对比，有限元解和《桥规》解的结果基本一致。

2)结论。

本文推导出了在六面体单元中考虑空间预应力钢束的等效刚度的计算方法，为运用实体单元对具有复杂形状几何形状的提供了一种可靠的方法。所用的计算方法精度较高，有明显的应用价值。

[1] 李亚智，赵美英，万小朋.有限元法基础与程序设计[M].北京:科学出版社，2004.

[2] [德]P.L.Kattan.Matlab有限元分析与应用[M].北京:清华大学出版社，2004.

[3] JTG D62-2004，公路钢筋混凝土与预应力混凝土设计规范[S].