特大跨度小净距隧道中间岩柱可靠度分析及其加固处理措施

胡金海，宋英龙，邹伟彪

(1.福州机场二期高速公路有限公司，福建福州 350002;2.同济大学地下建筑与工程系，上海 200092)

特大跨度小净距隧道中间岩柱可靠度分析及其加固处理措施

胡金海1，宋英龙2，邹伟彪2

(1.福州机场二期高速公路有限公司，福建福州 350002;2.同济大学地下建筑与工程系，上海 200092)

魁岐2号隧道位于福州国际机场高速公路二期工程A3标段，隧道跨度达到19.9 m，中间岩柱最小净距为11.7 m，为国内首座双向八车道小净距隧道工程。针对魁岐2号隧道工程的特殊性，利用离散单元法对节理岩体中特大断面小净距隧道的受力情况进行了分析，根据可靠度理论，通过对魁岐2号特大断面小净距隧道中间岩柱的可靠性分析发现，对于特大断面小净距隧道，中间岩柱最薄弱的部位主要集中在岩柱上部，因此，对于特大断面小净距隧道施工过程中宜重点对岩柱上部进行加固处理。同时，根据不同围岩级别中中间岩柱的可靠度值显示，魁岐2号特大断面小净距隧道的净距取值基本上是合理的，整体上能满足稳定性的要求。

大跨度隧道;小净距;中间岩柱;节理;可靠度;离散元;UDEC;加固措施;魁岐2号隧道

0 前言

结构可靠性是用可靠度来度量的。结构可靠度定义为在规定的时间内和规定的条件下结构完成预定功能的概率，表示为Ps，相反，如果结构不能完成预定的功能，则称相应的概率为结构失效的概率，表示为Pf。结构的可靠与失效为两个互不相容事件，因此，结构的可靠概率Ps与失效概率Pf是互补的，即:Ps+Pf=1，用概率来描述工程结构的可靠性既科学合理，又能得出定量指标。

自A.M.Freudenthal［1］将可靠度分析方法正式引入工程结构领域以来，结构可靠度分析的理论及方法得到了很大的发展，已出现多种计算可靠度的方法［2］:全概率法、矩法、数值模拟方法、随机有限元法、响应面法、结构体系可靠度计算方法等。

对于大断面小净距隧道，支护参数设计的一个非常重要方面，就是对中间岩柱进行加固支护设计。其目的主要是为了最大限度的保证中间岩柱的完整性，以提高开挖过程中围岩的自承自稳能力。故一定程度上，小净距隧道设计、施工成功与否的关键就在于对中间岩柱加固处理的方法和效果。因而，对施工过程中岩柱的力学性态、加固支护方案，对中间岩柱结构可靠度的研究，自然成了研究人员关注分析的重点对象。

隧道中间岩柱结构系统可靠度当前仍然是结构可靠度分析中的难题。目前国内外所研究的结构系统可靠度分析方法都是将真实结构的原型受力情况作了相当程度的简化，对真实结构原型受力情况进行可靠性分析非常困难，目前还无法实现，另外，在已提出的系统可靠度分析方法的实用性方面，还有失效模式的建立(破坏准则)、寻找主要失效模式及相关性等方面还存在许多问题。因而，隧道系统可靠度分析比之地面结构更为困难，需要进一步研究以便解决这些存在的问题。

目前，常用的非连续岩体数值分析方法有两种:离散单元法DEM(Distinct Element Method)和非连续变形分析方法DDA(Discontinuous Deformation A-nalysis)。非连续变形分析方法DDA是基于岩体介质非连续性发展起来的，以模拟复杂加载条件下离散块体系统的不连续大变形的力学行为为目的的平行于有限元法的一种数值方法。离散单元法DEM将所研究的区域划分成一个个分立的多边形块体单元，单元之间可以看成角－角接触、角－边接触或边－边接触，而且随着单元的平移和转动，允许调整各单元之间的接触关系，最终，块体单元达到平衡状态，也可能一直运动下去。王贵君等［3］应用离散单元法对节理裂隙岩体中不同埋深无支护暗挖隧洞的稳定性及其变形机理进行了数值分析;廖巍等［4］用离散单元法模拟分析了围岩节理不同方位组合对巷道稳定性的影响及破坏形式;王贵君［5］采用离散单元法，对节理裂隙岩体中大断面隧洞围岩及支护结构的共同作用及施工过程力学状态，进行数值分析;荣冠［6］在分析彭水地下厂房地质条件的基础上，采用3DEC程序建立了三维离散元数值计算模型，对地下厂房开挖支护全过程进行了计算，详细分析了围岩变形情况、应力状态、塑性区分布及稳定性影响因素。

本文依托福州长乐国际机场高速公路二期工程魁岐2号双向八车道特大跨度小净距隧道工程，结合其复杂的节理岩体及其非连续性的特点，利用离散元软件对节理岩体中不同围岩级别中隧道施工后的应力状态计算结果以及岩体强度参数定义其破坏度，进而求得其可靠度指标。由于中间岩柱在施工过程中的力学行为特征，对围岩稳定性和支护结构参数选取起着决定性作用，保证小净距隧道中间岩柱的稳定是小净距隧道设计、施工的关键，故根据可靠度分析结果提出岩柱加固处理的建议。

1 工程概况

魁岐2号隧道位于福州国际机场高速公路二期工程A3标段，隧道长度为746 m，该隧道最大开挖跨度约19.9 m、拱高10.94 m、含仰拱总高度12.84 m，单洞标准断面内轮廓面积(路面以上)128.97 m2，含仰拱面积为159.49 m2。开挖毛洞中间岩柱净距11.7～15.3 m，即(0.59～0.77)B(B为隧道最大开挖跨度)［7］，图1为隧道设计断面尺寸示意图。按照《公路隧道设计规范》(JTG D70－2004)［8］中分离式独立双洞的最小净距规定以及国际隧道协会断面划分标准［9］，该隧道属于特大断面小净距隧道，同时类似于本隧道断面之大、结构之复杂，在国内外隧道工程中也是极为罕见。

图1 隧道设计断面尺寸

隧道场址区属低山丘陵地貌，地形起伏大，基岩大多直接裸露。洞身围岩以微风化花岗岩为主，围岩级别为Ⅲ～Ⅱ级;进出洞口的围岩以强、弱风化花岗岩为主，围岩级别为Ⅳ～Ⅴ级。本文针对性的选取出口段Ⅴ级围岩浅埋隧道部分代表性进行分析。

勘探资料［10］表明，隧道修建区域节理裂隙发育，通过对隧道Ⅴ级围岩掌子面节理进行调查、统计和拟合分析发现围岩中共存在如下3组优势节理［11］:(1)节理组1:节理倾角约为61°，平均间距为0.74 m;(2)节理组2:节理倾角约为53°，平均间距为0.85 m;(3)节理组3:节理倾角约为73°，平均间距为1.26 m。

2离散元计算模型

离散单元法是专门用来解决不连续介质问题的数值模拟方法，该方法把节理岩体视为由离散的岩块和岩块间的节理面所组成，允许岩块平移、转动和变形，而节理面可被压缩、分离或滑动。因此，离散元法比较适合用来研究节理岩体中相关工程问题。

根据魁岐2号特大断面小净距隧道的赋存条件，采用离散元数值分析软件UDEC4.0［12］对其破坏过程进行数值计算分析。计算模型中隧道埋深约为50 m，围岩级别为Ⅴ级。依据隧道开挖尺寸的影响范围，模型的左右边界约为隧道开挖跨度的5倍，上边界至地表自由面，并假设地表为水平状态，下边界至开挖洞底距离约为5倍洞高，两侧边界条件采用水平方向单向位移约束，底部边界条件采用水平方向和垂直方向双向位移约束。并根据工程地质概况建立如图2所示的数值计算模型。

图2 平面计算模型

模型中岩块假定为理想弹塑性介质，符合Mohr－Coulomb弹塑性模型，由于岩体的抗拉强度远低于其抗压强度，因此在离散元UDEC中Mohr－Coulomb弹塑性模型集合了Mohr－Coulomb强度准则和拉破坏屈服准则，即当岩体所承受的拉应力超过其抗拉强度时，岩体材料即发生拉破坏。模型中节理采用Coulomb平面接触滑动模型，岩石和节理的变形强度参数根据魁岐2号隧道地质资料选取［10］，如表1所示。

表1 岩石及节理力学性质参数

3 可靠度指标的计算

隧道作为地下结构，其真实的受力情况非常复杂，影响受力的各种随机变量的统计特征没有收集全，对各种失效模式的认识还较初步，因而隧道系统可靠度分析比之地面结构更为困难。因此，本文结合节理岩体特点及上述离散元模型的计算结果，可靠度计算过程如下。

(1)利用离散元对节理岩体中不同围岩级别中隧道施工后的应力状态计算结果以及岩体强度参数定义其破坏度为:

其中:σf可根据式(2)和式(3)求得。

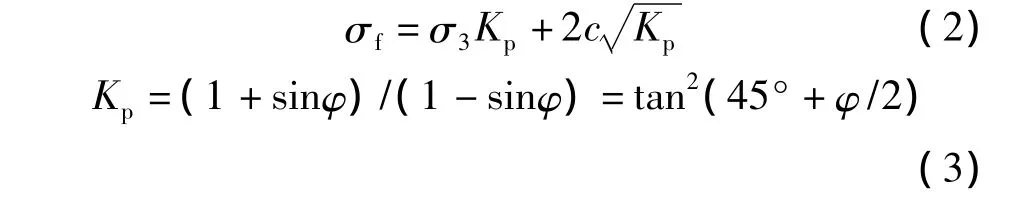
式中:σ1——计算所得到的最大主应力;σ3——计算所得到的最小主应力;c——岩体的粘聚力;φ——岩体的内摩擦角。

(2)由于η是表示围岩的接近破坏度的量值，所以称其为破坏接近度。一般认为当η=1时，中间岩柱已破坏;当η＜1时，中间岩柱未破坏。而如果把中间岩柱净距减小到破坏度完全贯通即η=1时作为评判中间岩柱是否破坏的标准，显然是不合理的，因为，此时中间岩柱已处于破坏的临界状态，若仅仅依靠外界加固的作用，必定会大大增加工程造价。因此，认为小净距隧道中间岩柱的破坏接近度应避免η=0.7的区域贯通［9］。

(3)由于破坏接近度和可靠度之间的关系，即: Ps+Pf=1，从而可以得出中间岩柱的可靠度，根据小净距隧道中间岩柱的破坏接近度应避免η=0.7的区域贯通的原则可知中间岩柱可靠度标准为Ps≥0.3。

在对魁岐2号隧道中间岩柱可靠度分析时，仍然采用在中间岩柱中布置监测点的方法对小净距隧道中间岩柱的状态进行监测，同时为了比较全面掌握中间岩柱的赋存状态，在对依托工程魁岐2号中间岩柱可靠度分析时，选取中间岩柱中心处及其距中心处左右各3 m处特征点为研究对象，具体特征点选择如图3所示。

图3 中间岩柱可靠度分析特征点布置图

4 计算结果及其分析

用离散元数值分析软件UDEC4.0对其破坏过程进行数值计算，通过对小净距隧道中间岩柱布置的监测点的状态进行监测，得出依托工程魁岐2号特大断面小净距隧道不同围岩级别条件下中间岩柱特征点的可靠度值如表2、图4所示。

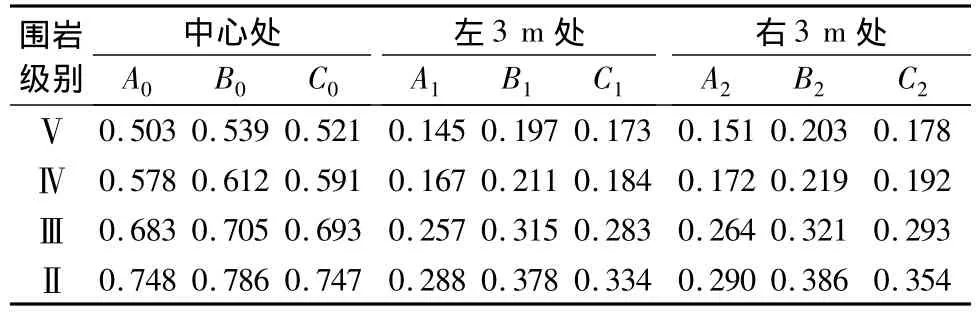
表2 中间岩柱特征点的可靠度值

图4 不同围岩级别中特征点可靠度

分析以上对依托工程魁岐2号特大断面小净距隧道不同围岩级别中中间岩柱特征点的可靠度数值，可以得出如下规律:

(1)随着隧道围岩岩性的改善，中间岩柱的可靠度逐渐提高;对于同一级别围岩，中间岩柱的上部可靠度最低，中间岩柱的底部可靠度次之，而中间岩柱的中部可靠度最高，这也说明了对于特大断面小净距隧道，中间岩柱最薄弱的部位主要集中在岩柱上部，因此，对于特大断面小净距隧道施工过程中宜重点对岩柱上部进行加固处理，这也是特大断面小净距隧道受力状况的一个重要特征。

(2)中间岩柱中心处的可靠度最小值为0.503，满足应避免中间岩柱的可靠度0.3的贯通标准，说明依托工程魁岐2号特大断面小净距隧道的净距取值的设计是合理的。

5 岩柱合理加固方案分析

根据已有的工程实践和经验，针对中间岩柱所采用的加固措施主要有:超前注浆预加固、加长锚杆、对拉锚杆加固以及他们的组合等。

注浆预加固是广泛采用的一种方法，既可以单独应用于较大净距隧道(通常大于1B)中间岩柱的加固，也可与对拉锚杆、预应力锚杆结合应用于近距离的小净距隧道的岩柱加固。对于质量较差的围岩，岩柱进行注浆加固可以起到较好的效果，这主要与注浆对提高围岩参数效果明显有关，注浆后围岩抗拉、抗剪强度显著提高，尤其对于裂隙发育的岩体，注浆后浆液充填裂隙及软弱结构面，可以避免或减小应力波在岩体内反射及折射引起岩体内部拉伸破坏，起到了很好的加固作用。对于质量较好的围岩，由于可注浆性要差，提高围岩力学性质参数较为困难，因此采用注浆加固要慎重。

水平对拉锚杆通常用于隧道净距在6 m以下的中间岩柱，且可适当施加预应力，超过6 m时可用系统锚杆替代，且在岩柱部分可适当加长。水平预应力对拉锚杆对裂隙可起到闭合的作用，并可有效阻止岩体内部质点的相对位移，避免造成拉伸破坏，提高其抗拉、抗剪强度。对于质量较差的围岩，由于其变形较大，若采用预应力锚杆会产生较大的预应力损失，与一般普通锚杆效果相差不大;相反，对于质量较好的围岩，由于其变形较小，采用预应力加固效果较好。

因此，根据对特大断面小净距隧道岩柱可靠度分析结果，随着隧道围岩级别的差异，也仅从定性的角度按质量较差的围岩、质量较好的围岩分别对加固措施进行探讨和说明。

对于Ⅳ～Ⅵ级等质量较差的围岩，岩柱加固以注浆方式为主，辅以锚杆支护综合选取。在此种围岩中，大断面小净距隧道其岩柱上部即雁形部应力状态相对最差，因此，对该部位进行相关加固处理是非常必要的，可以较好的改善和提高岩柱及隧道的整体稳定性。

需要说明的是，岩柱底部拱脚部位应力状态也相对较差，如果把注浆范围扩大至拱脚，显然可以较好的改善其应力状态，但是一般来说它对洞室的整体稳定性影响不大，而且仰拱开挖支护回填后，拱脚的变形、塑性区的发展均可以得到非常有效的抑制和控制，而从注浆加固的工程实践和经济性方面考虑，一般也很少对拱脚部进行注浆加固。重点是对岩柱雁形部采用注浆加固和预应力锚杆加固等方式，加固示意如图5所示。

图5 岩柱注浆加固区范围及雁形部锚杆支护示意图

6 结语

福州长乐国际机场高速公路二期工程魁岐2号隧道为特大断面小净距隧道，且隧道修建区域节理极其发育，本文通过离散元软件对特大跨度小净距隧道中间岩柱可靠度分析，得到如下结论。

(1)随着隧道围岩岩性的变好，中间岩柱的可靠度逐渐提高;对于同一级别围岩，中间岩柱的上部可靠度最低，中间岩柱的底部可靠度次之，而中间岩柱的中部可靠度最高，说明了对于特大断面小净距隧道，中间岩柱最薄弱的部位主要集中在岩柱上部，这也是特大断面小净距隧道受力状况的一个重要特征。

(2)中间岩柱中心处的可靠度最小值满足中间岩柱的可靠度的标准，说明依托工程魁岐2号特大断面小净距隧道的净距取值的设计是合理的。

(3)通过对可靠度计算结果分析，提出了中间岩柱加固的合理建议:重点是对中间岩柱雁形部采用注浆加固和预应力锚杆加固等方式，而可靠度同样相对较低的岩柱下部则没有必要进行注浆加固。

［1］A.M.Freudenthal.Safety of Structures［J］.Trans.ASCE，1947，112.

［2］谢圣纲.大跨度隧道施工围岩稳定性及可靠度研究［D］.重庆:重庆大学，2006.

［3］王贵君.节理裂隙岩体中不同埋深无支护暗挖隧洞稳定性的离散元法数值分析［J］.岩石力学与工程学报，2004，23(7): 1154－1157.

［4］廖巍，徐海清，刘贵应.岩体结构面组合对巷道围岩稳定性的影响［J］.安全与环境工程，2004，11(2):65－67.

［5］王贵君.节理裂隙岩体中大断面隧洞围岩与支护结构的施工过程力学状态［J］.岩石力学与工程学报，2005，24(8):1328－1334.

［6］荣冠.彭水地下电站围岩稳定性分析［J］.岩土力学，2007，(S1):855－859.

［7］福建省交通规划设计院.福州长乐国际机场高速公路二期工程(A3标段)两阶段施工设计［R］.福建福州:福建省交通规划设计院，2007.

［8］JTG D70–2004，公路隧道设计规范［S］.

［9］龚建伍.扁平大断面小净距公路隧道施工力学研究［D］.上海:同济大学，2008.

［10］福建省交通规划设计院.魁岐2号隧道工程地质评价［R］.福建福州:福建省交通规划设计院，2007.

［11］陈孝湘.特大跨度隧道岩体节理精细化采集描述及其块体稳定性研究［D］.上海:同济大学，2009.

［12］Itasca Consulting Group，Inc.UDEC universal distinct element code(Version 4.00)user’s guide［R］.Minneapolis，USA: Itasca Consulting Group，Inc.，2004.

Reliability Analysis on Middle Rock Pillar in Small Clear Space Tunnels with Super Span and the Reinforcement Measures

HU Jin-hai1，SONG Ying-long2，ZOU Wei-biao2(1.The Second Phase Project of Fuzhou International Airport

Highway Corporation，Fuzhou Fujian 350002，China;2.Department of Geotechnical Engineering，Tongji University，Shanghai 200092，China)

Kuiqi No.2 tunnel is belonged to tender section A3 of the phase II project of Fuzhou International Airport Highway.It is the first small clear space tunnel project for 8 lanes in China with the span of 19.9 meters and with the middle rock pillar of minimum clear distance about 11.7 meters.According to the specialty of Kuiqi No.2 tunnel and based on discrete element method，some numerical simulation analysis is conducted to analyze the initial surrounding rock stress to the tunnel.The results show that the worst position of mechanical state in large-section tunnel is in the upper portion of middle rock pillar in weak surrounding rock，so special reinforcement measures should be used there.According to the reliability value of middle rock pillar in different rock mass，the net distance between Kuiqi No.2 small clear space tunnels with super span is reasonable to satisfy the stability requirement.

super span tunnel;small clear space;middle rock pillar;joint;reliability degree;DEM;UDEC;reinforcement measures;Kuiqi No.2 tunnel

U443.15

A

1672－7428(2012)03－0077－05

2011－08－22

胡金海(1966－)，男(汉族)，福建仙游人，福州机场二期高速公路有限公司董事长，公路与城市道路专业，从事工程建设管理工作，福建省福州市，fz.hjh@163.com。