光行差对恒星时的影响分析

郭思远，林 翔

(北京环球信息应用开发中心，北京 100094)

光行差对恒星时的影响分析

郭思远，林 翔

(北京环球信息应用开发中心，北京 100094)

光行差是观测者的运动速度与星光的运动速度相结合(相对运动)产生的一种光学效应。各种光行差对恒星的观测均会产生影响,本文阐述了周日光行差和周年光行差对恒星坐标(主要是赤经)的影响，并进一步分析光行差对地方恒星时产生的影响。

周日光行差；周年光行差；地方恒星时

在天文测量中，天体的坐标会由于自然界某些因素的影响而发生一些不明显的微小变化，产生这些变化的主要因素有大气折射、视差、光行差、岁差、章动等。任一瞬间测站的地方恒星时等于该瞬间天体的赤经与时角之和，即为该瞬间春分点的时角。由于光行差对天体观测的坐标变化，因此也会产生时间观测的变化。

1.地方恒星时的计算

星时是以地球自转周期为基准建立的一种时间系统。天体的周日视运动周期是地球自转的反映，若测定地球自转的周期，可在天球上选一天体或某一特殊点作为参考点，并以观测站的子午圈作为量度参考点的周日视运动周期的参考(或起算)方向。显然，参考点连续两次通过该地子午圈的时间段，即为地球自转的一个周期。现选取春分点γ作为参考点，用它的周日视运动周期所确定的时间计量单位，称为恒星时，简称恒时，常用S表示。

1.1恒星时(s)与春分点时角(tγ)的关系

春分点γ与天体σ同时做周日视运动(见图1)，当春分点γ上中天(在上点Q)时，其时角tγ=0h，测站恒星时s=0h；之后，tγ随着γ的周日视运动而逐渐增大，恒星时S也相应地增大，直到γ第二次上中天又在Q点时，t=24h，此时s=24h。由此可知，任一瞬间的恒星时s在数值上等于这瞬间春分点的时角tγ，即s=tγ。

图1

1.2 恒星时与天体的赤经和时角的关系

春分点的时角tγ等于某天体的赤经与时角之和，即

tγ=α+t

(1)

s=α+t

(2)

若已知某一恒星的σ的赤经为α，则只要测定它在某一瞬间的时角t，则可用(2)求出观测瞬间的恒星时s。当恒星σ上中天时，t=0h，则

s=α

(3)

由此可知，任何瞬间的恒星时正好等于该瞬间上中天恒星的赤经。

2.光行差的概念

在观测天体时,天体的光线是沿着直线方向按照一定的速度(光速)射进望远镜的视野。光行差就是观测者的运动速度与星光的运动速度相结合(相对运动)而产生的一种光学效应。

在图2中，假设观测者在E点用望远镜EO观测一个不动的天体σ0，若观测者在空间也是静止不动的，则看到天体σ0的方向Eσ0的方向是它的真方向，真方向指向天球上的一点σ就是这天体的真位置。如果观测者以速度v沿EA方向运动，则此时天体σ0相对于观测者而按速度-v沿着与EA相反的σ0F方向运动；与此同时，天体的光线又以光速c沿着σ0E的方向射向观测者。因此，这两种运动的合成使天体的光线变为沿σ0H方向运动，从而使观测者此时看到天体的方向不是真方向Eσ，而是与σ0H平行的视方向Eσ′。这种由于星光的运动和观测者的运动相结合而使天体的方向发生变化的现象，称为光行差现象。而由此所得的天体视方向Eσ′与其真方向Eσ之差α=∠σ′Eσ，称为天体的光行差。由于光行差使天体在天球上的位置由σ移至σ′，这一光行差位移的方向是朝向观测者的运动方向EA与天球相交的A点。这个A点称为光行差位移的奔赴点或向点。

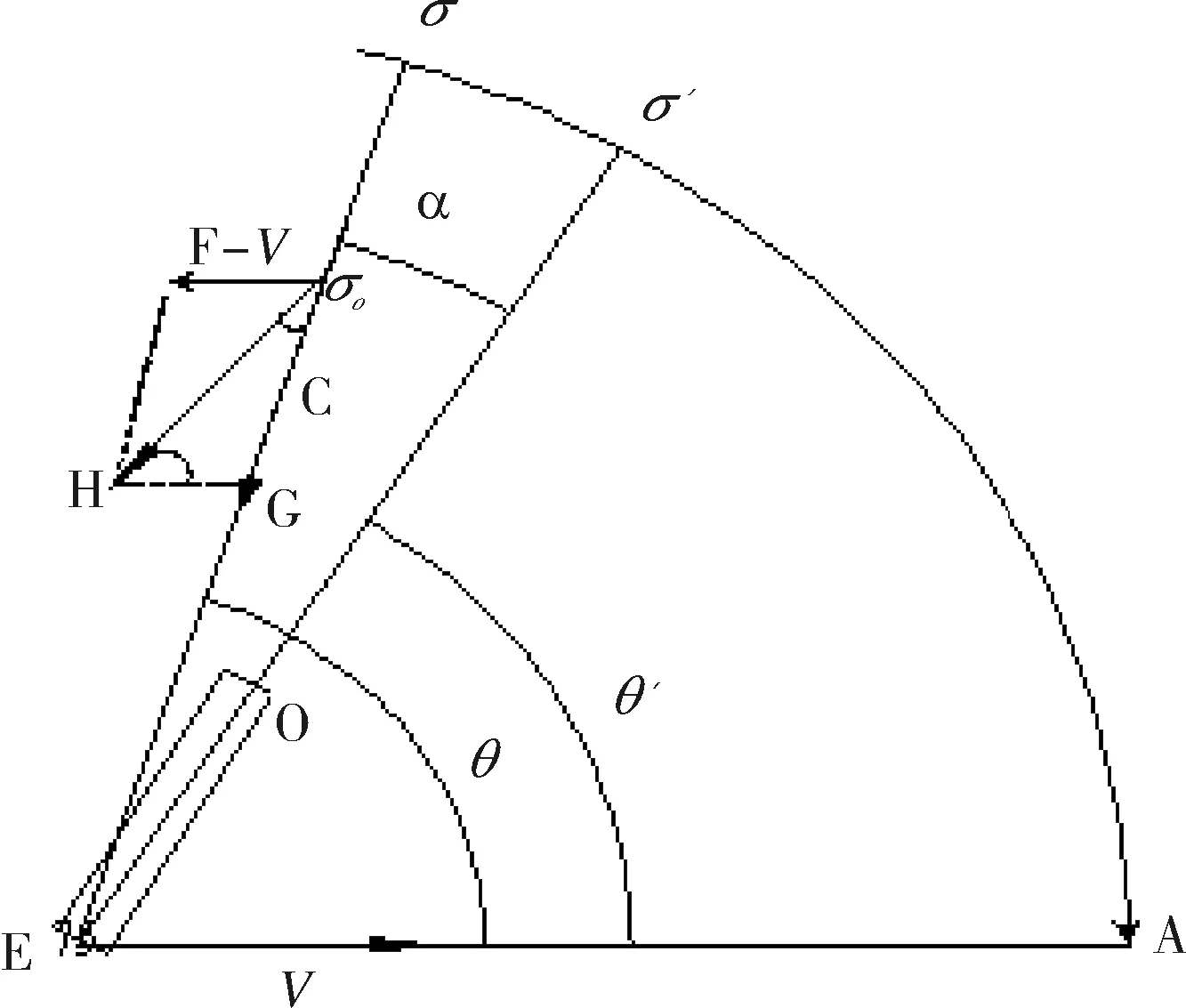
图2

为了推出求α的一般表达式，设天体的视方向Eσ′和真方向Eσ分别与观测者运动方向EA的夹角为θ′和θ，于是在三角形σ0HG中，按正弦定律得：

sinα=(v/c)sinθ′

(4)

因α很小，可取sinα=α″/ρ″，并取θ(或σA)代替θ′，则(4)式可写为：

α=σσ′=ρ″(v/c)sinσA

(5)

令K=(v/C)ρ″=206265″(v/c)

(6)

K称为光行差常数，于是(5)式变为

α=σσ′=KsinσA

(7)

(7)式就是计算光行差a及光行差位移σσ′的一般表达式。由上讨论可知，光行差使观测天体的视方向总是向前倾斜了一个a角，从而使天体σ在天球上沿着通过该天体和奔赴点A的大圆弧朝向奔赴点A的方向位移了一段弧σσ′，这是光行差位移的一般规律。由(5)式也可看出，若光速c为无穷大或观测者在空间静止不动，即v=0，则光行差a=0。这说明光行差只有在光速c为有限值和观测者以一定的速度在运动的条件下才会发生。若取光速c为一常数，则观测者的速度越大，光行差a值也越大，即视方向向前倾斜得越大。

观测者在空间随地球的运动主要有三种：(1)地球自转；(2)地球公转；(3)地球随太阳系向武仙座方向的运动。因地球自转而产生的光行差称为周日光行差；因地球公转而产生的光行差称为周年光行差；因太阳系的运动所产生的光行差称为长期光行差，这种光行差对各恒星均有同样的影响，而且在几千年内太阳系运动的方向可视为不变，故这种光行差可不考虑。下面将分别讨论周日光行差，周年光行差以及从它们对恒星坐标的影响来分析对恒星时的影响。

3.光行差对地方恒星时的影响

恒星受光行差的影响而在天球上产生视位移，因此用来表示其位置的各种坐标也随之发生相应的变化，当恒星的赤经α发生变化时，其地方恒星时也将发生相应的变化。下面将分别讨论周日光行差和周年光行差对恒星赤经α的影响和由此产生的对地方恒星时计算的影响。

3.1 周日光行差对地方恒星时的影响

观测者随地球的自转运动与星光的运动相结合而引起的天体视位移，即为周日光行差。在图3中，P为北天极，Z为天顶，观测者的运动方向总是指向天球上的东点，因此东点E即为周日光行差的奔赴点。地球自转的方向是由西向东，观测者的运动方向总是指向天球上的东点，因此东点E即为周日光行差的奔赴点。在周日光行差的影响下，天体的真位置σ将沿通过天体的东点的大圆σE向东点位移σσ′。σ′为天体的视位置。设v为纬度为φ的测站M随地球自转的线速度，则按(6)式知周日光行差常数K=(v/c)×206265″，设地球半径为R，测站BMA的半径为r(r=R·cosφ)，则v=2πg/T=(2π·R·cosφ)/T，取地球自转周期T=86164平时秒(即一个恒星日)，地球半径R=6378km，可得v=0.465 cos φ km/秒，于是测站M的光行差常数为

K=(0.465cosφ/299792.5)×206265″=0″.3199cosφ

或K=0s.0213cosφ

(8)

在图4中，设σ(α,δ)为恒星在某一瞬间的位置，σ′(α′,δ′)为该星受周日光行差影响向东点E位移后的位置。σσ′为周日光行差位移。PT和PT′分别为σ和σ′的时圈。过σ′作大圆弧σ′D垂直时圈PT，在直角三角形中Pσ′D中，因α-α′和σ′D很小，按正弦公式并用secδ代替secδ′，则得

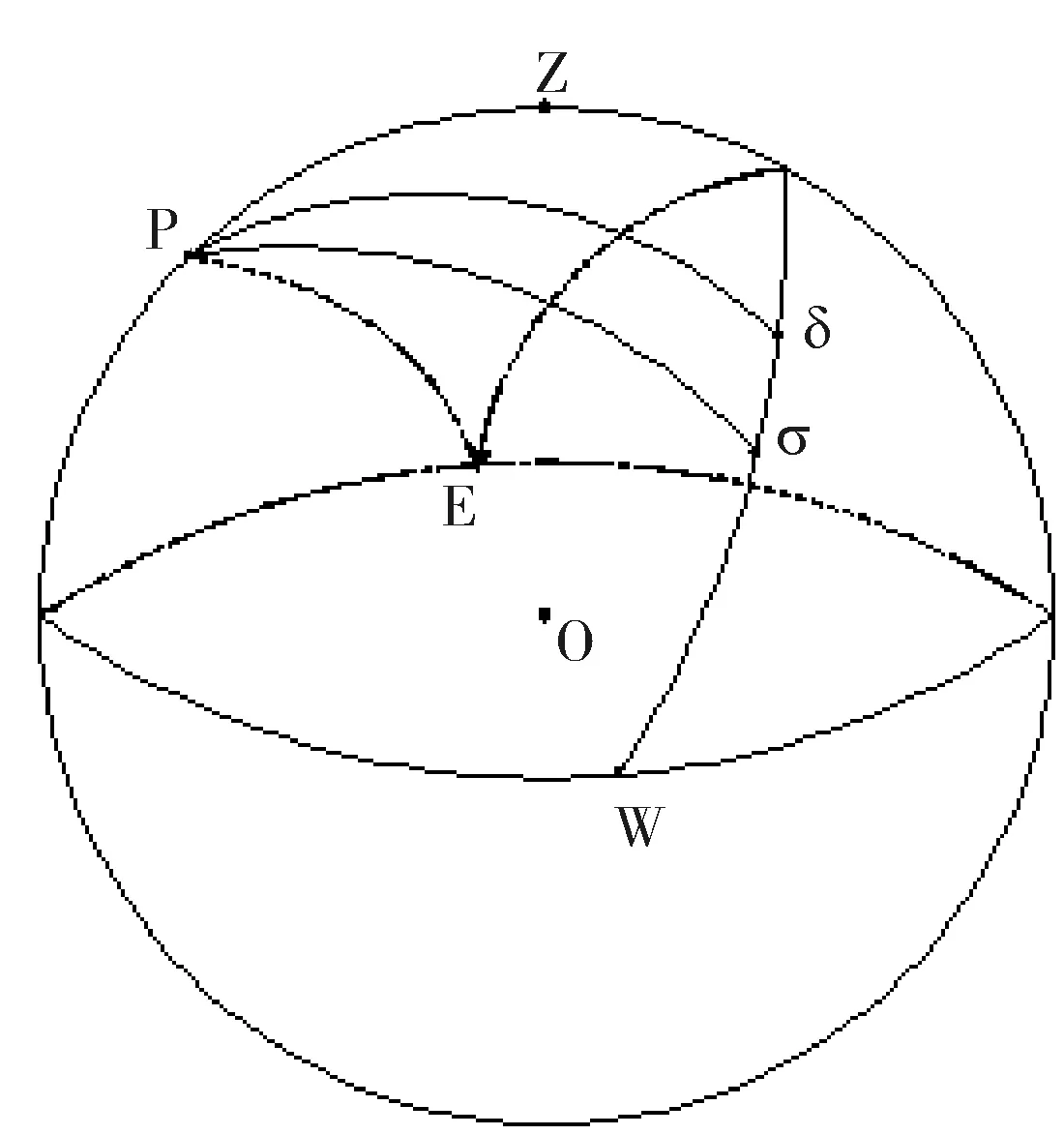
图3

图4

α-α′=σ′Dsecδ

(9)

又因σ′D很小，可视它为平行赤道的一段小圆弧，于是有

δ-δ′=σD

(10)

为了求得σD和σ′D，可视σσ′D为平面直角三角形，由(7)式和∠Dσσ′=∠PσE，可得：

σ′D=σσ′sinDσσ′=0″.32cosφ·sinσE·sinPσE

σD=σσ′cosDσσ′=0″.32cosφ·sinσE·cosPσE

将以上二式分别代入(9)和(10)式，于是得：

α′-α=0s.021cosφ·sinσE·sin PσE·secδ

δ′-δ=0″.32cosφ·sinσE·cosPσE

(11)

又在球面三角形Pσ中，PE=90°，Pσ=90°-δ，∠σPE=90°+t，根据正弦公式和五元素公式可写出下二式：

sinσE·sinPσE=cost

sinσE·cosPσE=sinδ·sint

于是得到计算光行差对恒星赤经α影响的公式为

Δαd=α′-α=0s.021cosφ·cost·secδ

(12)

因此，在周日光行差的影响下，恒星的赤经变化使地方恒星时的计算变为：

s=α′+t=α+Δαd+t

(13)

即s=α+0s.0.21cosφ·cost·secδ+t

(14)

3.2 周年光行差对地方恒星时的影响

(15)

式中T为恒星年，等于365.256366平太阳日，e为地球轨道偏心率，a为日地平均距离。式中T=31558150s.0，c=299792.48km/秒，a=1.000000236天文单位，1天文单位A=149600000km，e=0.016722。按(14)式算得周年光行差常数K=20″.496。在图5中，S为太阳，K为黄级，LL′为黄道，E为地球在某一瞬间的位置，其运动方向即该点的切线方向EA，这个方向在天球上的投影为A点，则A点就是周年光行差的奔赴点。如图5所示。

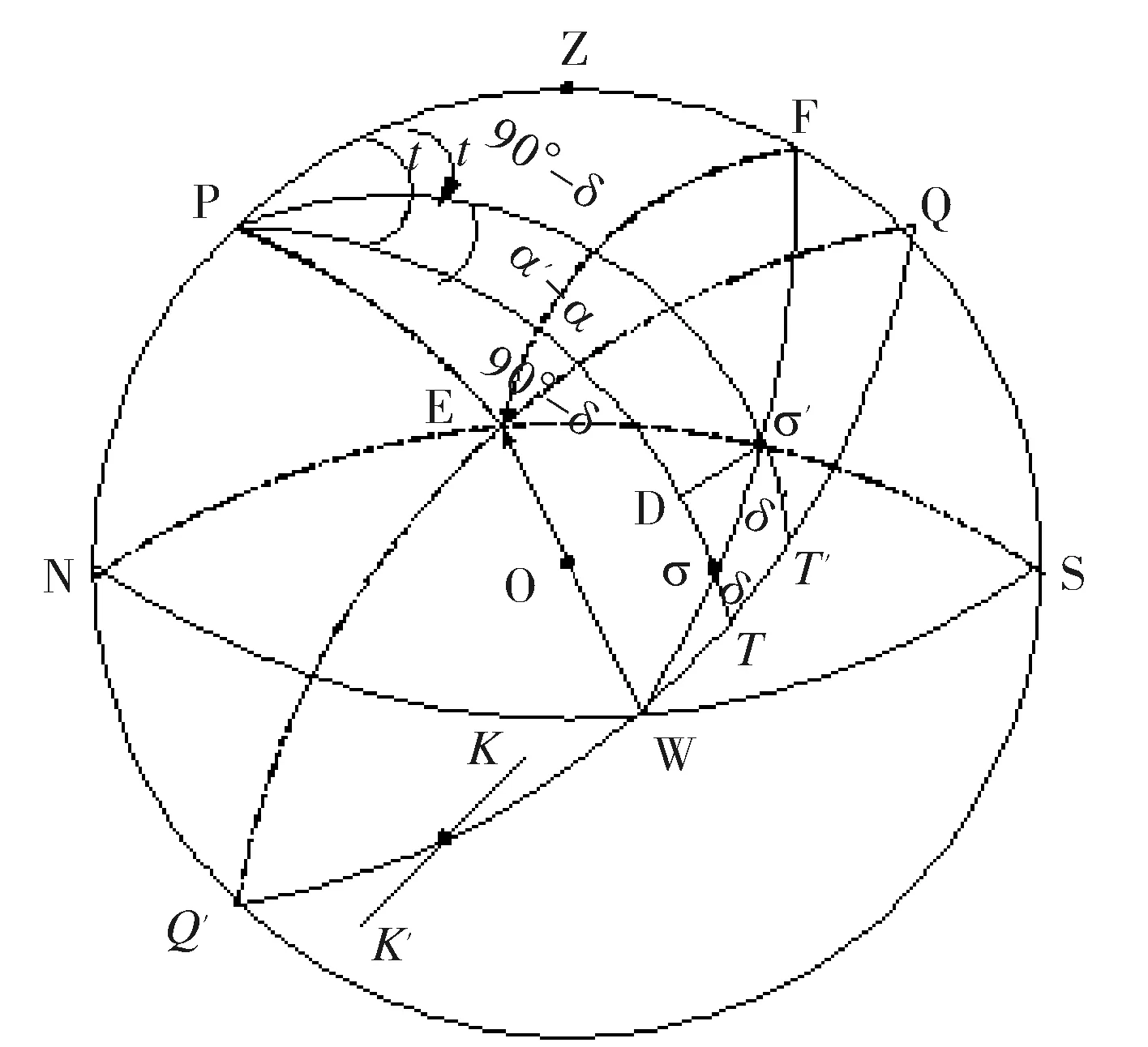
图5

图6

恒星受周年光行差的影响而在天球上产生视位移，因而其在天球上的坐标也随之发生相应的变化。在图6中，设σ(α,δ)为恒星在某瞬间的真位置，σ′(α′,δ′)为受周年光行差影响位移后的视位置。A为奔赴点，σσ′为恒星的周年光行差视位移。按(8)式知σσ′=KsinσA。过σ作小圆弧σD平行赤道QQ′。令Δαa=α′-α，Δδa=δ′-δ分别表示这一位移引起的恒星赤经，赤纬的变化，则有：

Δαa=α′-α=K·sinσA·cosΨ·secδ

Δδa=-(δ′-δ)=K·sinσA·sinΨ

(16)

又由球面三角形σPA得：

sinσA·cosΨ=cosδA·sin(αA-α)

-sinσA·sinΨ=sinδA·cosδ-cosδA·sinδ·cos(αA-α)

上式可写为：

sinσA·cosΨ=cosδA·sinαA·cosα-cosδA·cosαA·sinα

-sinσA·sinΨ=sinδA·cosδ-sinδ·cosδA·cosαA·cosα-sinδ·cosδA·sinαA·sinα

(17)

再由球面直角三角形γAQA可得：

sinl▯=cosαA·cosδA

sinδA=-cosl▯·sinε

-cosl▯·cosε=sinαa·cosδA

将上三式代入(16)式，则得：

sinσA·cosΨ=-cosl▯·cosε·cosα-sinl▯·sinα

-sinσA·sinΨ=-cosl▯·sinε·cosδ-sinl▯·sinδ·cosα+cosl▯·cosε·sinδ·sinα

=-cosl▯·cosε(tanε·cosδ-sinα·sinδ)-cosα·sinδ·sinl▯

再将二式代入(17)式，则得周年光行差对恒星赤经α的影响计算式为：

Δαa=-K·cosl▯·cosε·cosα·secδ-K·sinl▯·sinα·secδ

上式中l▯为太阳黄经因子，因此在周年光行差的影响下，恒星的赤经变化使地方恒星时的计算变为：

s=α+Δαa+t=α-K·cosl▯·cosε·cosα·secδ-K·sinl▯·sinα·secδ+t

4.结束语

由于受光行差的影响，恒星的坐标在天球上会发生变化，光行差使恒星赤经的变化导致地方恒星时也发生变化。经过分析计算可以得到以下结论：设恒星真位置的赤经为α，受光行差影响位移后的视位置为α′，Δαa为恒星受周日光行差影响位移后的赤经变化，Δαa为恒星受周年光行差影响位移后的赤经变化，在周日光行差和周年光行差的共同影响下，α′=α+Δαd+Δαa，即α′=α+0s.021cosφ·cost·secδ-K·cosl▯·cosε·cosα·secδ-K·sinl▯·sinα·secδ，因此，在进行精确的时间计算时，需加入相应的光行差改正数，以此来减弱光行差对恒星坐标(主要是赤经)的影响，使地方恒星时的计算更为精确。

[1]夏一飞，黄天衣.球面天文学[M].南京：南京大学出版社,1995.

[2]王琦.导航卫星定位系统与产品的市场发展现状与趋势[J].中国航天,2004(4).

[3]干国强,邱致和.导航与定位[M].北京：国防工业出版社，2000.

AnalysisoftheInfluenceofAberrationtoSiderealTime

GUO Si-yuan, LIN Xiang

(Beijing Universal Information Application Development Center, Beijing 100094, China)

Aberration is an optical effect of the combination of observer and stars’ velocity. This paper describes the impacts of diurnal aberration and annual aberration on stellar coordinates and analyzes aberrations’ influence on local sidereal time.

diurnal aberration; annual aberration; local sidereal time

2012-01-12

郭思远(1982—)，女，河南郑州人，硕士，北京环球信息应用开发中心助理工程师。

P12

A

1008-3715(2012)02-0122-04

(责任编辑吕志远)