基于MATLAB的秩亏自由网平差研究

周 蕴

(郑州市规划勘测设计研究院，郑州 450052)

基于MATLAB的秩亏自由网平差研究

周 蕴

(郑州市规划勘测设计研究院，郑州 450052)

针对传统经典平差固定基准存在的缺陷，研究基于MATLAB的秩亏自由网平差算法，在分析秩亏自由网平差函数模型和随机模型的基础上，运用MTLAB进行秩亏自由网平差，结果表明克服传统经典平差的不足，对变形监测数据进行更严密的平差，准确地给出所有观测点的误差，对指导变形分析有重要的应用价值。

MATLAB；秩；自由网；平差

MATLAB是由美国MathWorks公司推出的用于数值计算和图形处理的科学计算系统环境。MATLAB的英文全称是Matrix Laboratory，可直译为矩阵实验室。测量数据的处理特别是测量平差主要应用矩阵运算，而MATLAB又特别易于做矩阵运算，因此研究开发基于MATLAB的秩亏自由网平差具有极好的应用价值。

1.秩亏自由网平差数学模型

1.1秩亏自由网平差概述

经典平差中，都是以已知的起算数据为基础，将控制网固定在已知数据上。如水准网必须至少已知网中某一点的高程，平面网至少要已知一点的坐标、一条边的边长和一条边的方位角。当网中没有必要的起算数据时，我们称其为自由网，网中没有起算数据时的平差方法，即自由网平差。

函数模型为：

V=AX-l

(1)

随机模型为：

D=σ02Q=σ02P-1

(2)

在经典平差中，A为列满秩矩阵，而在自由网平差中，R(A)=t-d，d为秩亏数，在最小二乘原则下，求得法方程为：

NX=ATPl

(3)

R(N)=R(A)=t-d。由于N是奇异的，故法方程是相容方程，它可以有无数解。在经典平差里，满足误差方程的V有无数组，选择其中VTPV=min这组。可以运用相似的原理附加一个最小范数条件

XTX=min

(4)

从而得到法方程的唯一解。

X=N+ATPl

(5)

(5)式中，N+为N的伪逆，这就是基于广义逆矩阵原理的直接平差方法(即秩亏自由网平差)。

1.2 边角网秩亏自由网平差数学模型

1.2.1 观测边长误差方程

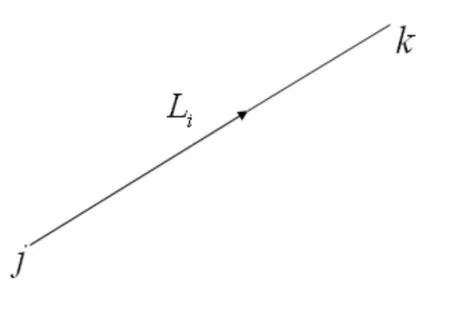
图1 边长观测示意图

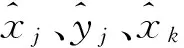
(6)

按泰勒公式展开，得

(7)

式中

令

(8)

可得测边的误差方程为

(9)

(9)式中右边前4项之和是由坐标改正数引起的边长改正数。(9)式就是测边坐标平差误差方程的一般形式，因在自由网中两端都是待定点，所以系数均不为0。

1.2.2观测方向误差方程

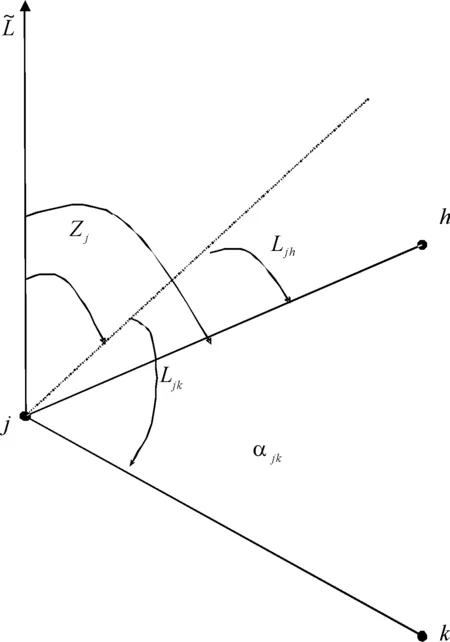
图2 方向观测示意图

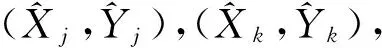
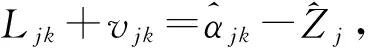
(10)

由近似坐标引起的近似坐标方位角的改正数为δαjk，即

(11)

将方位角改正数表达为坐标改正数可以利用

(12)

将(12)、(11)及

代入(10)式，即得jk方向的误差方程：

(13)

(13)式中常数项

1.2.3 边角网平差随机模型

确定边、方向两类观测的随机模型，主要是为了给定两类观测值的权比问题。边角网中各边长和各方向观测相互之间都是独立的，因此随机模型D=σ02Q=σ02P-1中的权阵是对角阵。设网中有n1个角度观测β1,β2,β3…,βn和n2个边长观测S1，S2，…,Sn,n1+n2=n,则权阵为

P=diag(pβ1,…,pβn1,ps1,…,psn2)

(14)

定权公式为：

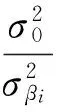
(15)

式中σβ1=σβ2=…=σβ。定权时一般令

(16)

即以方向观测中误差为边角网平差中的单位权观测值中误差，由此可得：

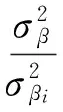
(17)

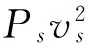
2.基于MATLAB的自由网平差

2.1 控制点的自动获取

为减少用户不干预的情况下进行平差计算，本文采用从原始观测文件获取控制点的方法。具体算法为：在边角网中，把所有点视为测站点或照准点，所以只需对边长和角度观测文件进行遍历并把点号存入相应数组中即可。

2.2近似坐标的计算

考虑到变形监测的边角网大多为边角同测网，在计算近似坐标时采用的是极坐标法，基本思路：若存在已知方位角，首先判断该方位角的起点是否是已知点A、终点是否是所求的待定点P，如果是，搜索边长AP即可按极坐标公式计算坐标；若没有已知方位角或其终点不是P，则搜索与P有方向观测的已知点A，再由A搜索另一个已知点B，且A到B有方向观测值，于是可求出AP的方位角，在搜索AP的边长观测值，由极坐标公式即可计算P点的坐标。

2.3平差计算和精度评定

在边角网的误差方程的线性化的过程中运用的是泰勒级数进行展开的，为保证平差结果的正确性，理论上说近似值应很接近坐标的真实值，这样引起的改正数误差才足够小。本文采用的是迭代趋近，直至坐标改正值小于0.1mm，这就保证了平差坐标的可靠性，为后续的变形分析提供可靠的依据。

3.秩亏自由网平差结果及分析

采用的数据为pad2002边角网算例(原网形如图 3)，进行自由网平差。平差结果见表1，表 2和表 3，验后平面单位权中误差=0.67s，迭代次数为3。

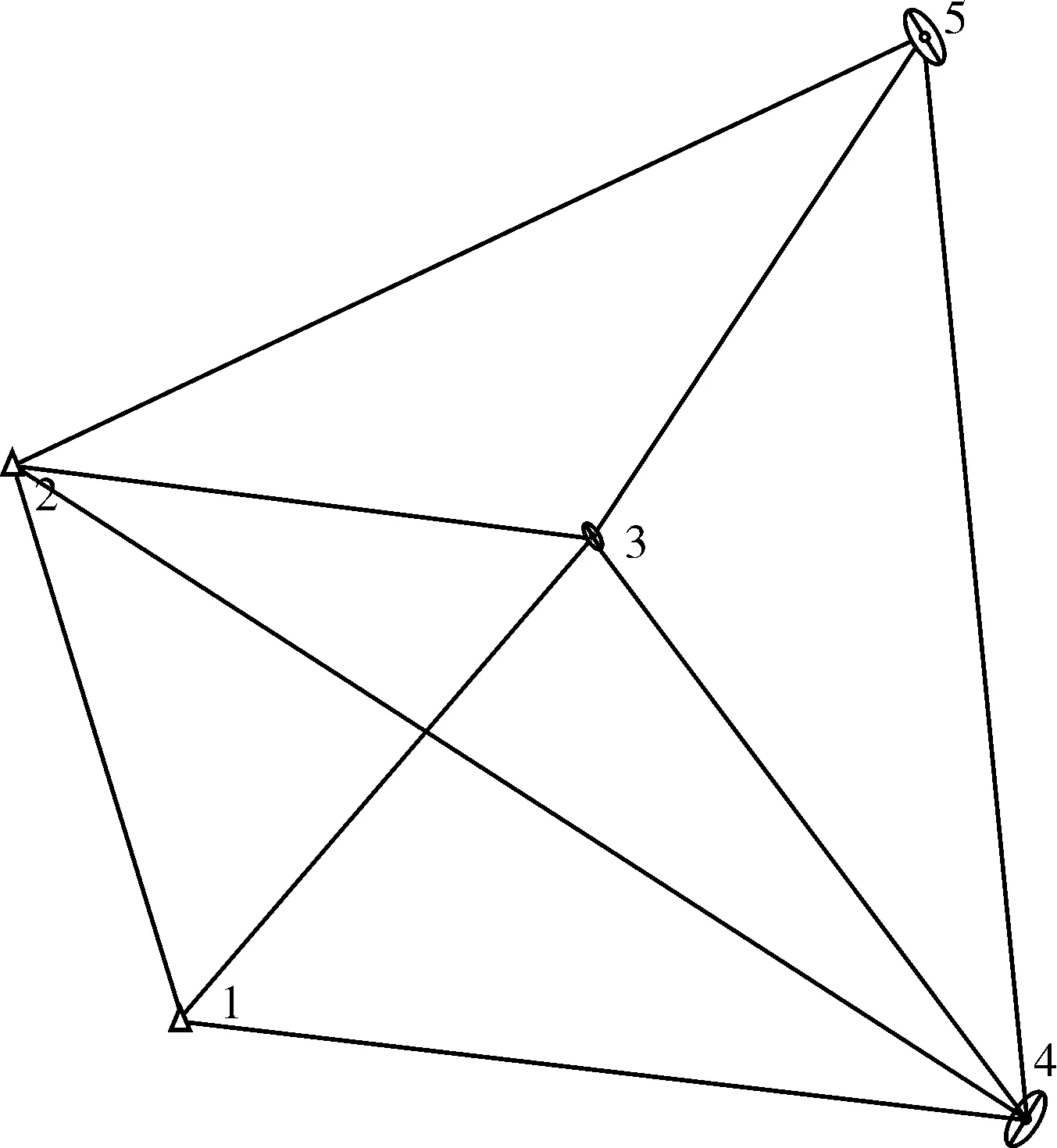
图3 采用算例边角网网形图

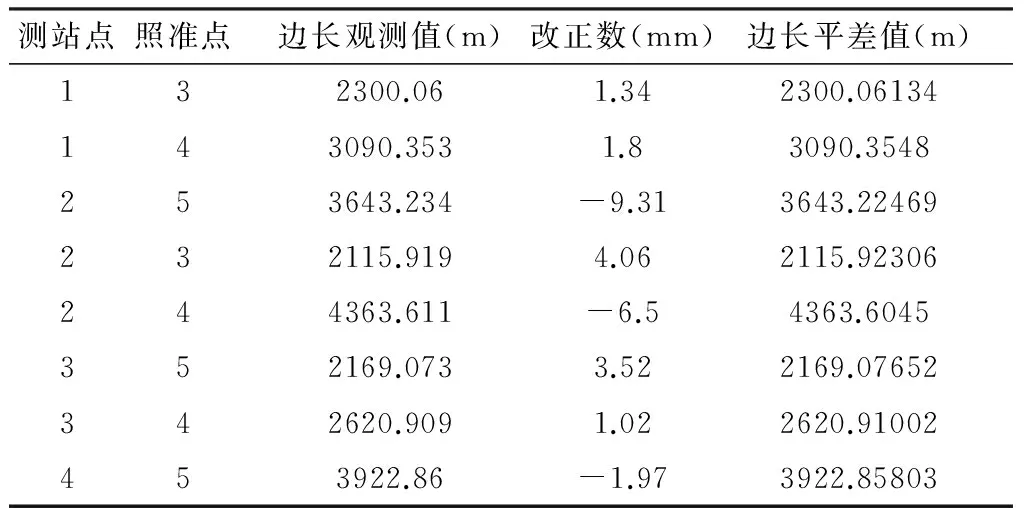
测站点照准点边长观测值(m)改正数(mm)边长平差值(m)132300.061.342300.06134143090.3531.83090.3548253643.234-9.313643.22469232115.9194.062115.92306244363.611-6.54363.6045352169.0733.522169.07652342620.9091.022620.91002453922.86-1.973922.85803

比较图 3和图 4不难看出，采用重心基准进行的秩亏自由网平差算法，有效克服了传统经典平差固定基准的缺陷，准确给出了所有观测点(含固定基准下已知点1，2)的误差并形象绘制了误差椭圆。为变形网的分析和变形监测数据的后处理提供了可靠的数据和准确快捷的图形分析依据。

4.结语

本文采用MATLAB开发的自由网平差程序克服了传统经典平差的不足，对变形监测数据进行了更严密的平差，准确的给出了所有观测点的误差。对指导变形分析和工程应用有着重要的实际意义和应用价值。

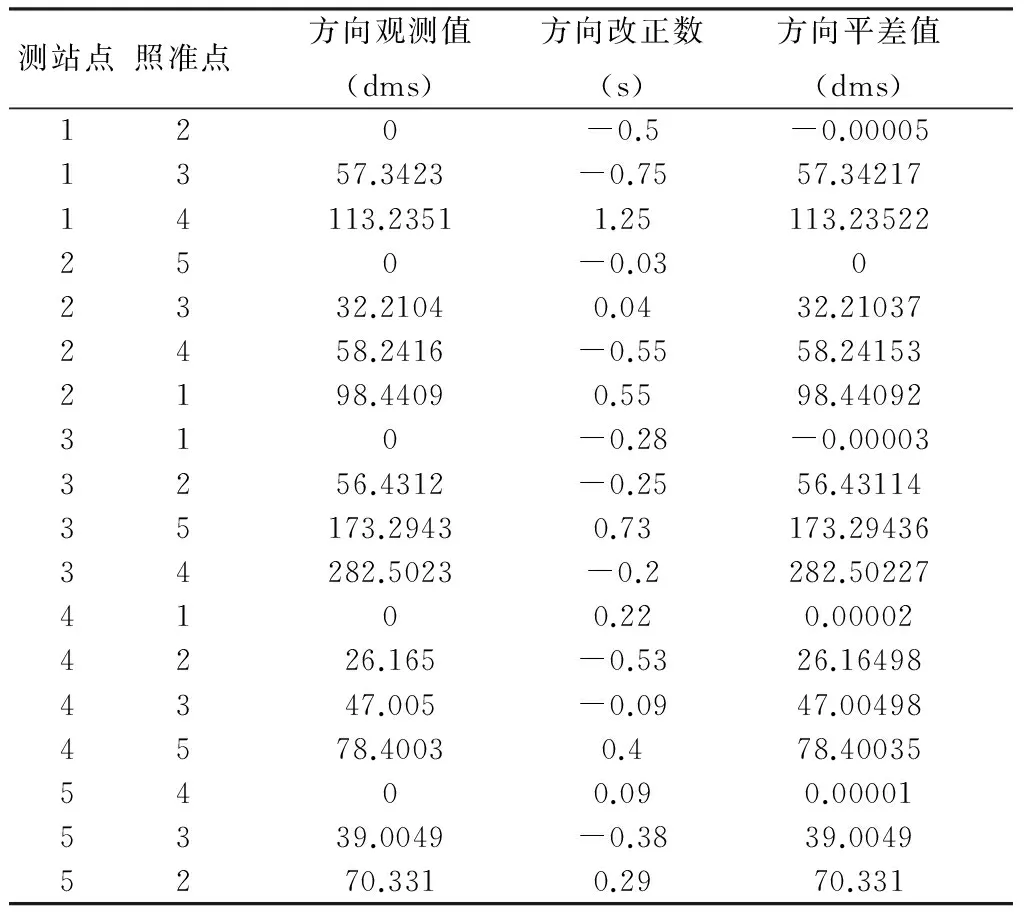
表2 方向平差结果

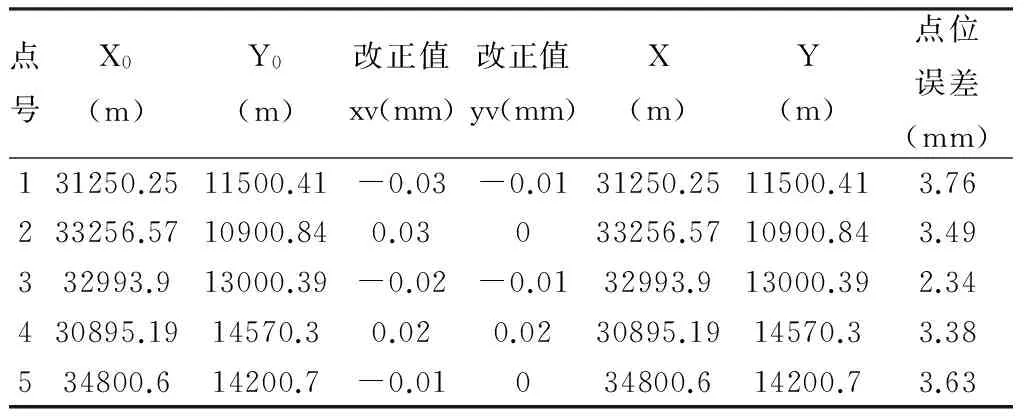
表3 坐标平差结果

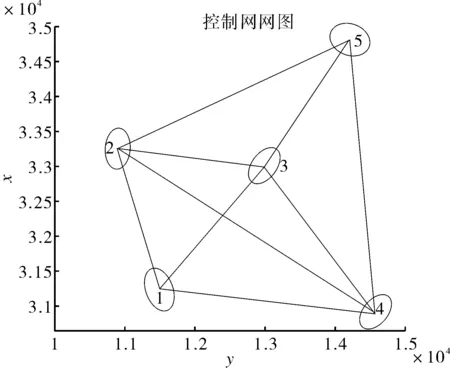
图4 边角网网形图及误差椭圆图(误差椭圆比例为100)

[1]刘卫国，陈昭平，张颖.MATLAB程序设计与应用[M].北京:高等教育出版社，2002.

[2]左廷英，刘庆元.MATLAB在测量控制网优化设计与平差中的应用[J].矿山测量，2003(2)：46-47.

[3]陶忠刚，王宝山，王勇，等.MATLAB软件在测量平差中的应用[J].焦作工学院学报，2002(5)：393-395.

[4]武汉大学测绘学院测量平差学科组.测量平差基础[M].武汉：武汉大学出版社，2003.

2012-01-14

周蕴(1979—)，男，湖南攸县人，郑州市规划勘测设计研究院工程师，主要从事测绘工程技术研究。

P228.4；TP319.9

A

1008-3715(2012)02-0119-03

(责任编辑吕志远)