基于改进粒子群算法的多目标单交叉口信号优化控制*
曹娟娟,邵 维
(长沙理工大学交通运输工程学院,湖南长沙 410004)
基于改进粒子群算法的多目标单交叉口信号优化控制*
曹娟娟,邵 维
(长沙理工大学交通运输工程学院,湖南长沙 410004)
交叉口信号配时优化,对缓解城市的交通拥堵,提高城市道路通行能力具有非常重要的意义.以各相位进道口上的停车次数、总延误和通行能力作为目标进行优化,并依据实时交通量数据来调节对应的权重系数,实现信号控制的自适应调节.模型的求解利用基于克隆选择的粒子群算法,得出信号配时方案,并与传统的webster算法作比较.
单交叉口;信号配时;多目标;克隆选择;粒子群优化算法
伴随着我国国民经济持续、快速发展,机动车拥有量急剧增加,这为交通运输行业带来了繁荣景象;然而,大多数城市的交通却处于相当紧张的状态,交通拥堵已成为大城市突出的社会问题之一.其中提高交通信号控制系统的科学性是城市道路交叉口智能监控系统研究的核心问题,对缓解日趋紧张的交通问题,减少交通事故和交通拥挤现状有着非常重要的意义.
针对城市道路交叉口的交通流特性,提出了多目标自适应优化控制方法,对单个交叉路口的不同优化指标(停车次数、延误时间、通行能力)进行分析建模,采用多目标改进粒子群算法求解,尽量满足单个路口的多个目标优化需求[1,2].
1 交通信号配时优化模型
1.1 信号控制目标分析
交叉口信号控制目标包括延误、饱和度、停车次数、通行能力、油耗、尾气排放、噪音、运营成本等.在这些目标中的基本量仅包括延误、停车次数、通行能力、饱和度、排队长度.其他的量均可以由基本量导出.因此本文仅以停车次数、延误、通行能力三个指标做为目标函数进行优化控制.
延误分析[3]:采用webster延误时间计算公式,总延误时间计算公式为:
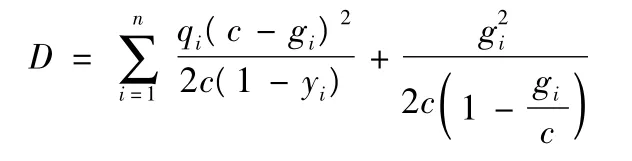
其中:C为信号周期(s);gi为相位i的有效绿灯时间;yi为交叉口第i相位交通流量与饱和流量之比;qi为相位i的车流量(pcu/h).
停车次数分析:交叉口车辆总的停车次数为:
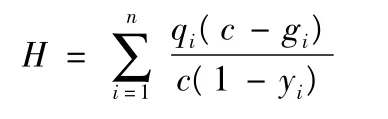
总的通行能力分析:信号交叉口的通行能力是指在一定的道路条件和交通管制条件下,某一入口车道单位时间内所
能通过的最大交通量,以车道为基本单位.
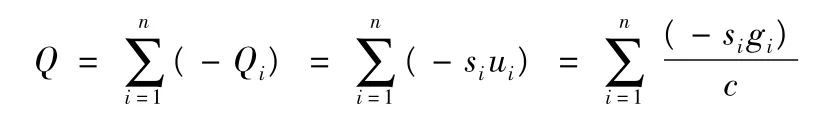
其中:Si为第i相位的饱和流量(pcu/h).
因为一天中交通需求量不断变化,所以对交叉口的信号配时的要求侧重点也不一样,在交通处于闲散或者顺畅的状态时,控制目标侧重于畅通舒适最大,即延误和停车次数最小;在交通处于繁忙或拥堵状态时,控制目标侧重于管理效率最高,即更偏重于通行能力最大.所以根据交通需求量的不同,调节三个目标函数的权重系数(随交通量不同而实时变化的性能指标),期望能使交叉口达到最好的交通状态.三个权重系数为:
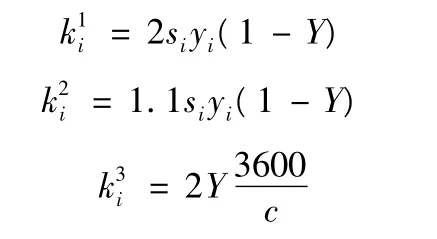
其中:Y为交叉口流率比.
1.2 交通信号配时建模
本文以典型的单交叉口四相为信号控制为例,交叉口有东西南北四个方向,每个方向都有直行、右转、左转三个方向的车流.具体相位信号控制方案如图1:
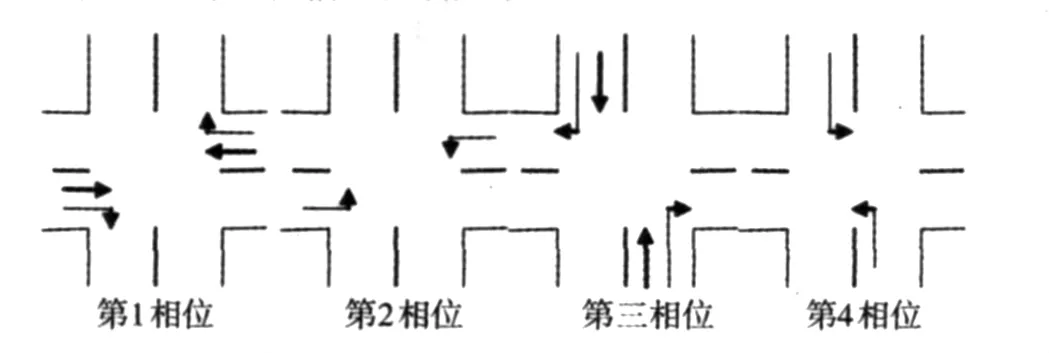
图1 典型四相位图
根据道路交通流数据,以总延误时间、停车次数最小和通行能力最大为目标,利用随交通量实时变化的权重系数,建立相应的目标优化函数如下:
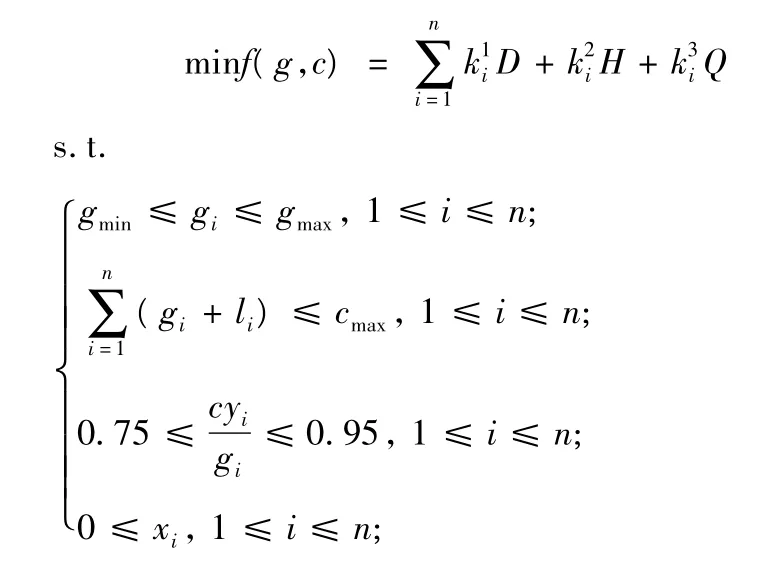
其中:gmin为相位i最小的有效绿灯时间,(s);gmax为相位i最长的有效绿灯时间,(s);li为相位i的损失时间,(s);cmax为最大周期时间,(s).
上述的约束条件约束了道路交叉口的饱和度k.为了避免饱和度过小,我们设定参数0.75,同样为了避免饱和度过大,设定参数0.95,它们的取值是可变的.
2 基于克隆选择的粒子群算法
2.1 粒子群算法基本介绍
粒子群算法(PSO)是一种新发展起来的,进化的优化算法.这种算法最开始是由Eberhart博士和kennedy博士提出来的.在这种算法中,有一种我们称为“粒子”的东西,它类似于鸟类捕食活动中的一只鸟,即我们优化问题中得一个解.每一个粒子都有一个相对应的适应值,这种适应值是被优化的函数决定的.除此之外,每个粒子还有它们飞翔的方向和距离,这个是由一个可变的速度决定的.最后这些粒子就进行搜索,它们的搜索是通过在整个解的空间中跟踪着当前的最优粒子进行的.
PSO首先会产生一些随机粒子(随机解).随后粒子会在整个空间中寻找并且相互之间会进行比较,进行更新,这样通过一次次的迭代寻找到全局的一个最优解.在各次迭代中有两个最优解,粒子会不断地寻找这两个最优解并且更新自己.其中一个是当前在全部群体中可以找到的最优解,这个称为全局最优解gbest,而另外一个是粒子自己找到的最优解,这个称为个体最优解pbest.在粒子寻找最优解时,粒子会自动更新自己的速度和位置,更新的公式如下:
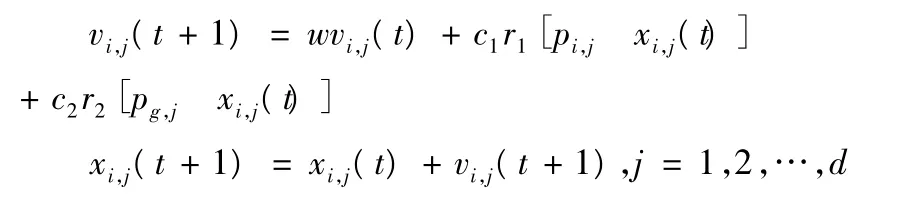
其中:c1和c2为学习因子,取正数;w为惯性权因子,根据需要优化的目标函数取适当的值;r1和r2取0-1之间的随机数,随机数是呈均匀分布的.
2.2 基于克隆选择的粒子群算法
粒子群算法也存在很多缺陷,比如在算法运行中,会出现“聚集”现象.这种现象是指当其中一个粒子找到了一个目前最优解,那么其余的粒子将迅速地向那个聚集.这样会导致群体发散.除此之外,还容易出现搜索精度低,结果是局部最优解的结果,我们称之为早熟收敛现象[4,5].
基于克隆选择的PSO算法的原理:将克隆选择机制融入粒子群算法中,最开始随机产生一些粒子;然后算出各个粒子的适应度值,并且比较得到的适应度值,根据优劣甄选出个体最优解pbest和全局最优解gbest;再来把算法中的粒子看作是克隆选择算法中的抗体并且算出它的亲和度.克隆复制我们挑选出的亲和度高的抗体(粒子),再变异那些复制后的抗体(粒子);最后更新粒子的位置和速度.
算法设计:
(1)初始化
随机初始化整个种群中的各个微粒的原始位置和速度.
(2)适应度
计算各个微粒的适应度值并且比较得到的适应度值,根据它的优劣甄选出个体最优解pbest和全局最优解gbest,判断是否满足条件,若满足结束条件,则停止运行并输出结果.否则继续.
(3)计算抗体(粒子)的偏好度.
由上所得的粒子的位置、速度、适应度等值,把第i个粒子的偏好力定义如下:
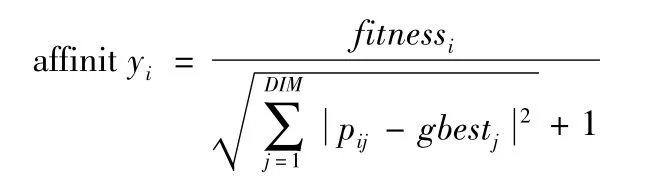
第i个微粒与全局最优微粒在第j维上的位置分别由pij与gbestj表示.因此,粒子的适应度值越小,粒子与与最优解离得越远,所以它的偏好力就越小,相反则越大.
(4)克隆复制
在整个群体中,根据上述所得到的微粒偏好力的大小对各个粒子执行克隆操作,这种操作要求是独立的、按比例的.第i个粒子被克隆(复制)的数量为
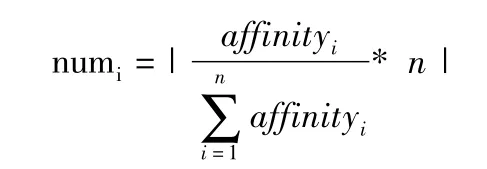
当中n是种群大小.因此,粒子的偏好力越大就越优良,会克隆(复制)出更多的子微粒,以此来保存比较优秀的个体.
(5)变异
对克隆(复制)的各个子微粒,要判断是否执行克隆高频变异,判断的依据为概率大小.进化中加入克隆高频变异,提供了粒子飞出局部极值的可能.
(6)克隆选择
为了避免算法退化,我们需要混合父代粒子与子代粒子.粒子经过克隆复制、变异后,从它的的父代粒子与子代粒子中,挑选出一个适应度值最高的最优粒子作为下一代粒子.
(7)粒子更新
更新粒子的速度和位置.
(8)判断
没有达到结束条件,返回步骤2.达到结束条件,算法结束.
3 仿真实例
以典型的四相位信号交叉口为例(信号控制方案如图1),对其相位的有效绿灯时间进行配时计算.假设交叉口的车流有关数据如表1.
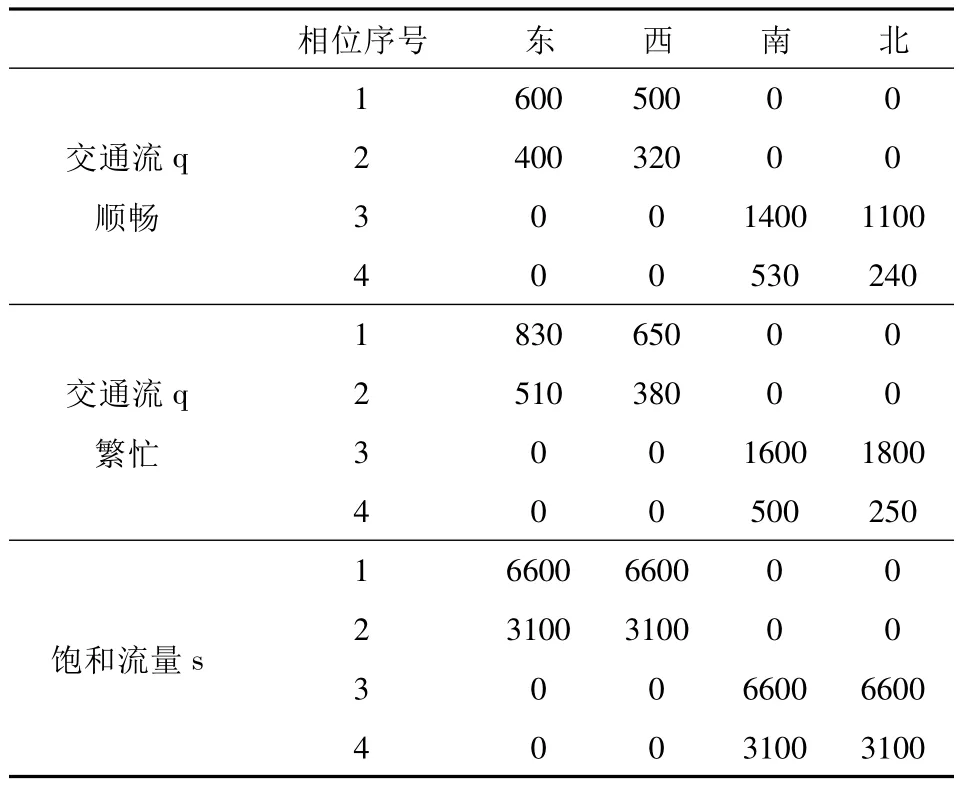
表1 交通状态顺畅、繁忙时各方向交通流数据
参数设置如下:初始群体规模为20,最大迭代次数为500 次,惯性权值为0.65,加速常数为 c1=c2=1.5.
其中,交叉口各相位的最小和最大有效绿灯时间定为10s和90s,最大周期时间为180s,总的损失时间为24s.
采用webster算法和基于克隆选择的粒子群算法求解信号配时方案.计算结果整理得到表2.
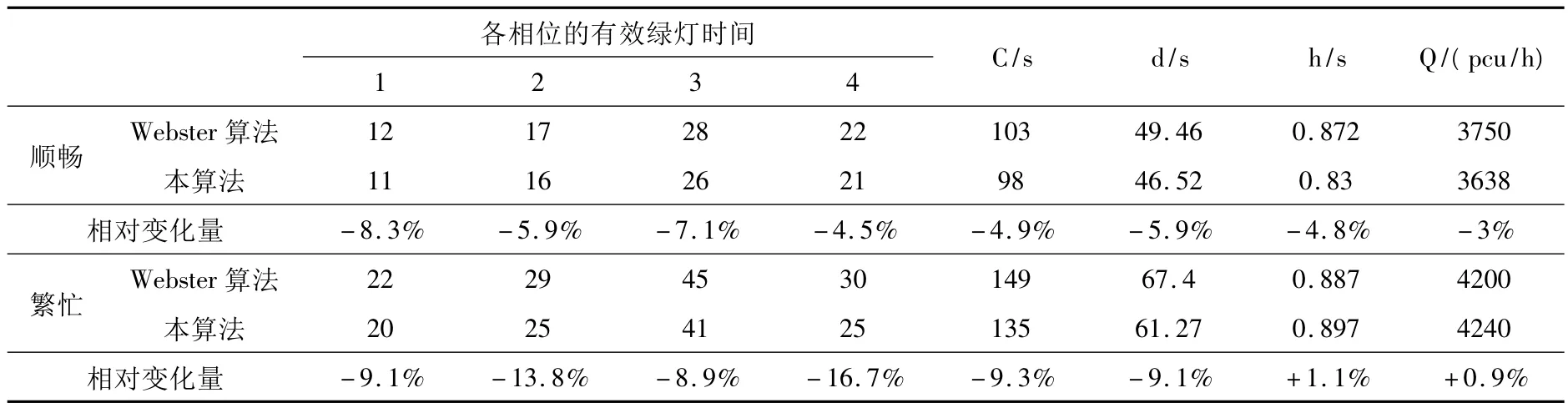
表2 两种算法的优化效果比较
4 结论
从结果可以看出,提出的基于克隆选择的粒子群算法更能实现各状态下减少停车次数和延误,增大通行能力的目标.将本算法与webster算法得出的结果进行比较,车辆的停车次数、延误和通行能力等指标都得到改善,而且针对交通流的到达规律对目标函数进行优化求解,从而得出最优交通信号配时方案,使各个方向到达的交通流能够在最合理的周期时间和最恰当的相位内顺利地通过交叉路口,满足实际的交通控制需求.在算法性能方面,该算法在标准粒子群算法中融合了克隆选择算法思想,增加了种群的多样性,加快算法收敛速度,提高最优解的精度.
[1]李晓娜.单交叉口自适应控制方法的研究[D].大连:大连理工大学硕士学位论文,2006.
[2]万伟,陈锋.基于遗传算法的单交叉口信号优化控制[J].计算机工程,2007,(16):217 -219.
[3]顾怀中.交叉口交通信号配时模拟退火全局优化算法[J].东南大学学报(自然科学版),1998,(3):68 -72.
[4]陈群,晏克非.基于遗传算法的城市交叉口实时信号控制研究[J].交通与计算机,2005,(1):15 -18.
[5]刘丽珏,蔡自兴.基于克隆选择的粒子群优化算法[J].小型微型计算机系统,2005,(9):1708 -1710.
U41
A
1008-4681(2012)02-0069-03
2011-11-08
曹娟娟(1987-),女,重庆人,长沙理工大学交通运输工程学院硕士生.研究方向:交通运输规划与管理.
(责任编校:晴川)

