过驱动飞行器积分滑模容错控制方法
鲍额尔敦, 王小平, 董新民, 陈勇
(空军工程大学 工程学院, 陕西 西安 710038)
过驱动飞行器积分滑模容错控制方法
鲍额尔敦, 王小平, 董新民, 陈勇
(空军工程大学 工程学院, 陕西 西安 710038)
针对过驱动飞行控制系统中执行器故障时的协调分配问题,提出了一种基于积分滑模的容错飞行控制器设计方法。引入虚拟控制思想,构造了多执行器故障条件下飞行器层级结构控制的数学模型。运用小增益定理,推导了系统闭环稳定的充分条件,并基于线性矩阵不等式,建立了最优状态反馈的凸优化模型。以积分滑模面切换函数为变量,选取李雅普诺夫能量函数,设计了渐近稳定的积分滑模控制器。仿真结果表明,该方法可综合考虑执行器完好和故障时的控制效能,能够实现多操纵面容错飞行控制,具有较好的鲁棒性。
过驱动飞行器; 容错控制; 控制分配; 积分滑模
引言
随着现代大型军、民用飞机对安全性、可靠性的要求,以及第四代歼击机对高机动性、高敏捷性和高隐身性的要求不断提高,飞机在结构布局上广泛采用多个独立的操纵面组合,尤其是诸多创新型操纵面和推力矢量技术的引入,使飞机具有较高的控制冗余度,即使在某些执行器发生故障的情况下,仍然可通过其他正常操纵面的重新组合来协同控制飞机,顺利执行任务并成功返航着陆。
控制分配技术[1-11]具有充分考虑操纵面的偏转约束、且在故障情况下进行控制重构时不需改变飞行控制律的优点,是近年来国内外学者用于处理飞行器多操纵面控制问题的关键技术。针对执行器故障情况下的控制分配问题,Ye等[2]采用LMI方法研究了F-16飞机执行器故障自适应容错跟踪控制问题;Zhang等[3]针对ADMIRE飞机的执行器故障分别应用伪逆法和定点法进行了控制重构研究;Casavola等[4]基于序列最小二乘提出了一种自适应容错方案,实现了多执行器轮船的有效控制;Boskovic[5]等研究了F-18飞机操纵面故障情况下的综合控制问题,并应用变结构方法补偿其耦合非线性;Oppenheimer等[6]结合混合优化控制分配方法研究了X-40A的内环自适应重构控制问题;Alwi等[7]结合加权伪逆法和滑模控制理论研究了过驱动飞控系统的在线容错控制分配问题。
滑模控制作为一种特殊的变结构非线性鲁棒控制方法,具有对不确定性和外界扰动的不敏感性和鲁棒性,国内外学者已经将其用于处理部分执行器故障时的控制问题[7]。本文基于积分滑模方法与控制律分配技术研究过驱动容错飞行控制问题,提出了一种闭环稳定的控制方案。该方法的优点是:当舵面有故障或失效时,不需要改变积分滑模控制器的结构,且具有良好的鲁棒性。
1 问题描述
考虑包含多个操纵面的过驱动飞行控制器小扰动数学模型为:
(1)
式中,A∈Rn×n为状态矩阵;x∈Rn为飞行状态;B∈Rn×m为输入矩阵;uc∈Rm为伪指令向量;y∈Rp为输出变量;C∈Rp×n为输出矩阵;D∈Rp×m为传输矩阵。在实际执行器系统中,期望的伪指令由操纵舵机实现。
通常,执行器-力矩线性化模型可描述为:
uc(t)=Wu(t)
(2)
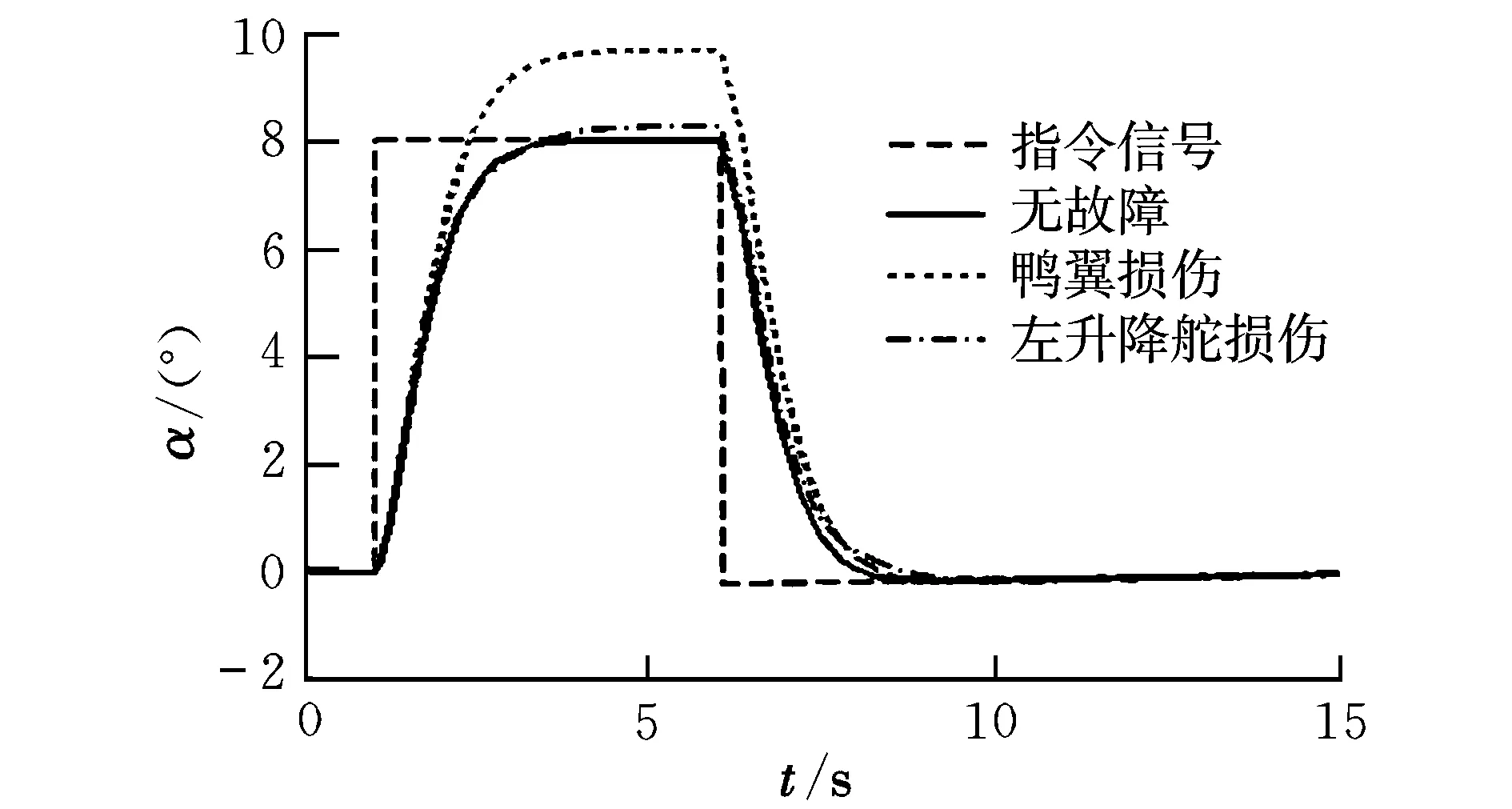
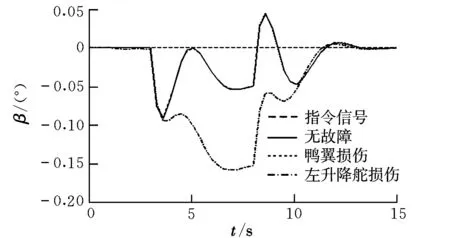
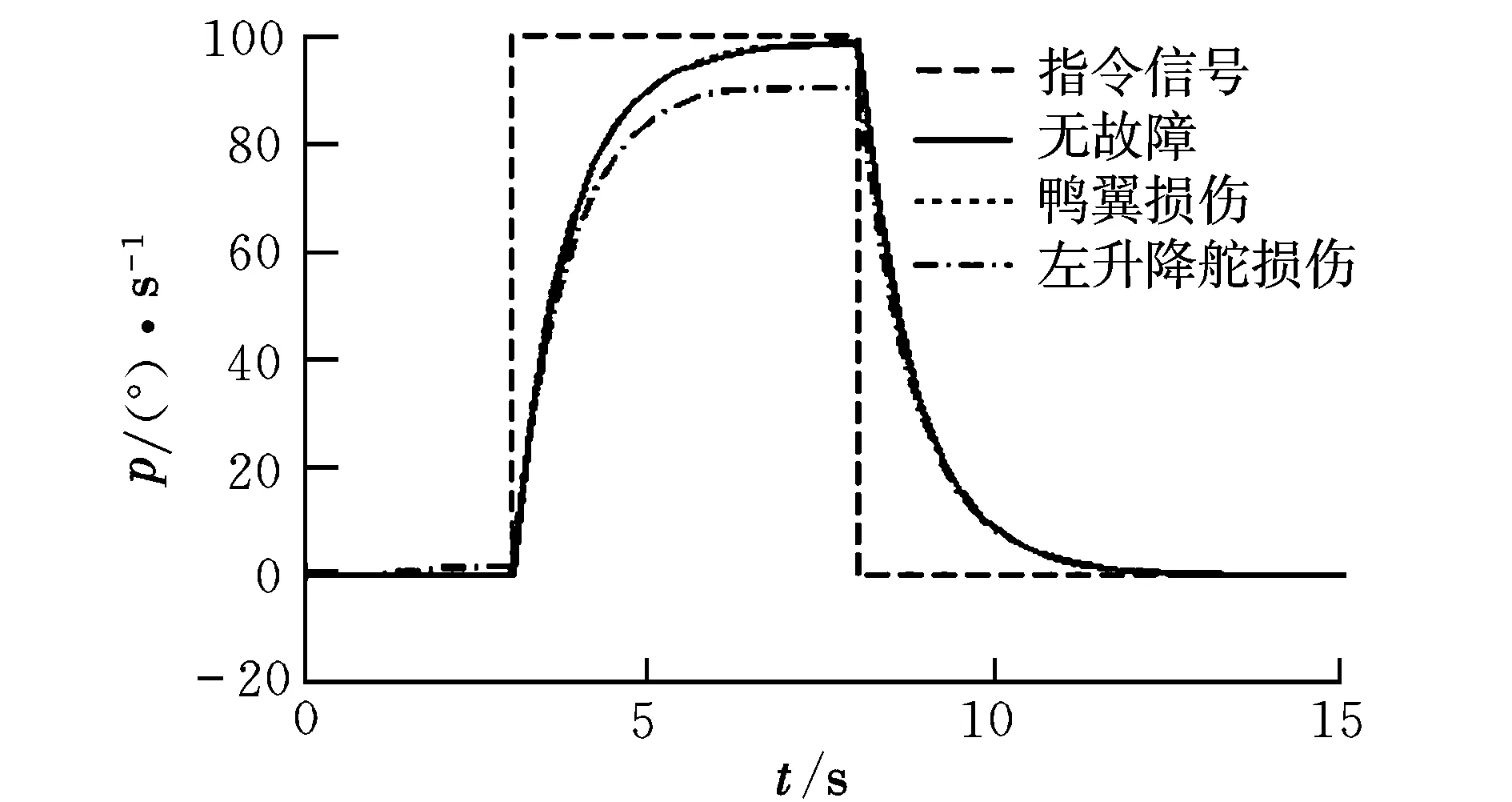
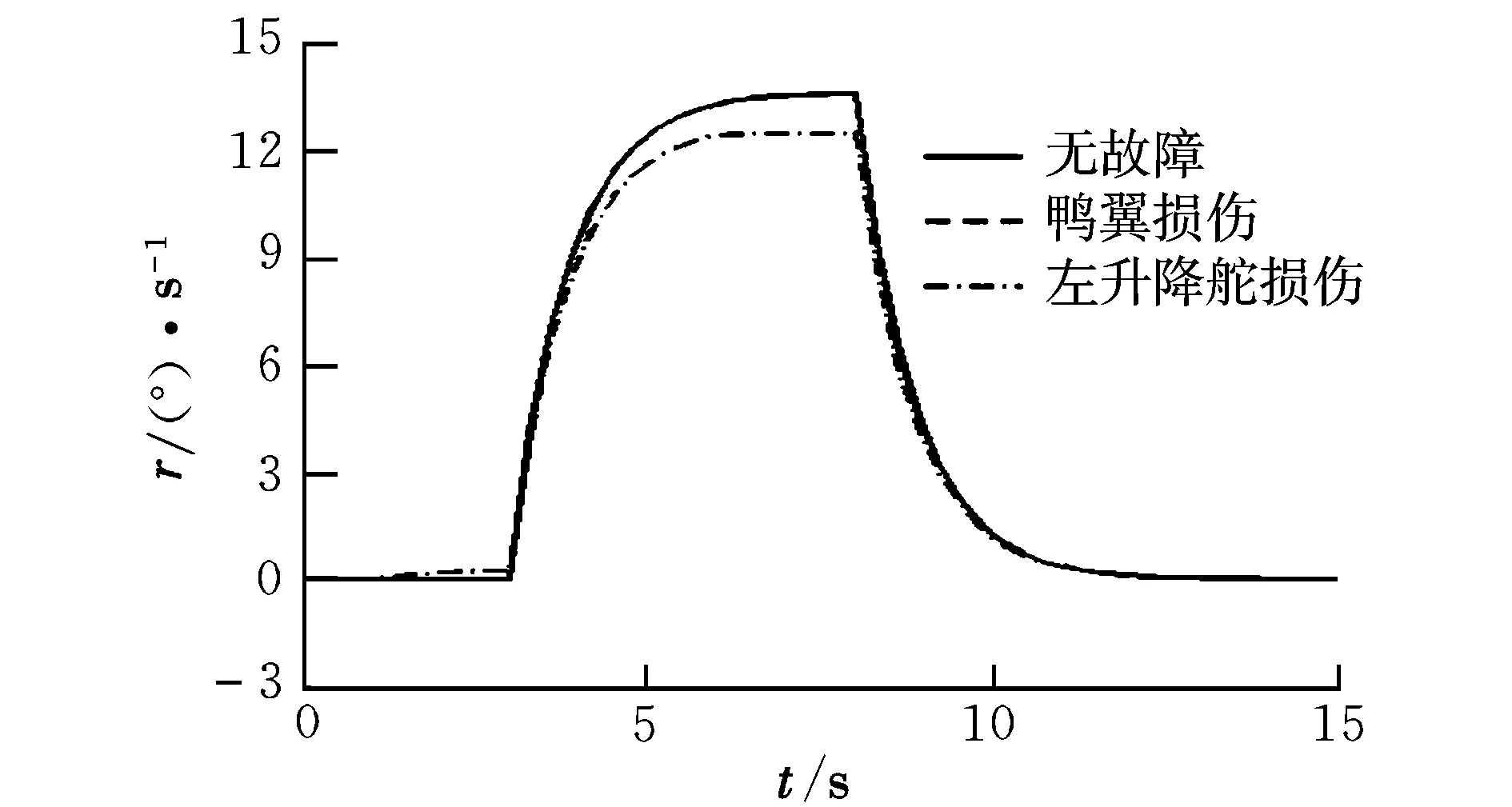
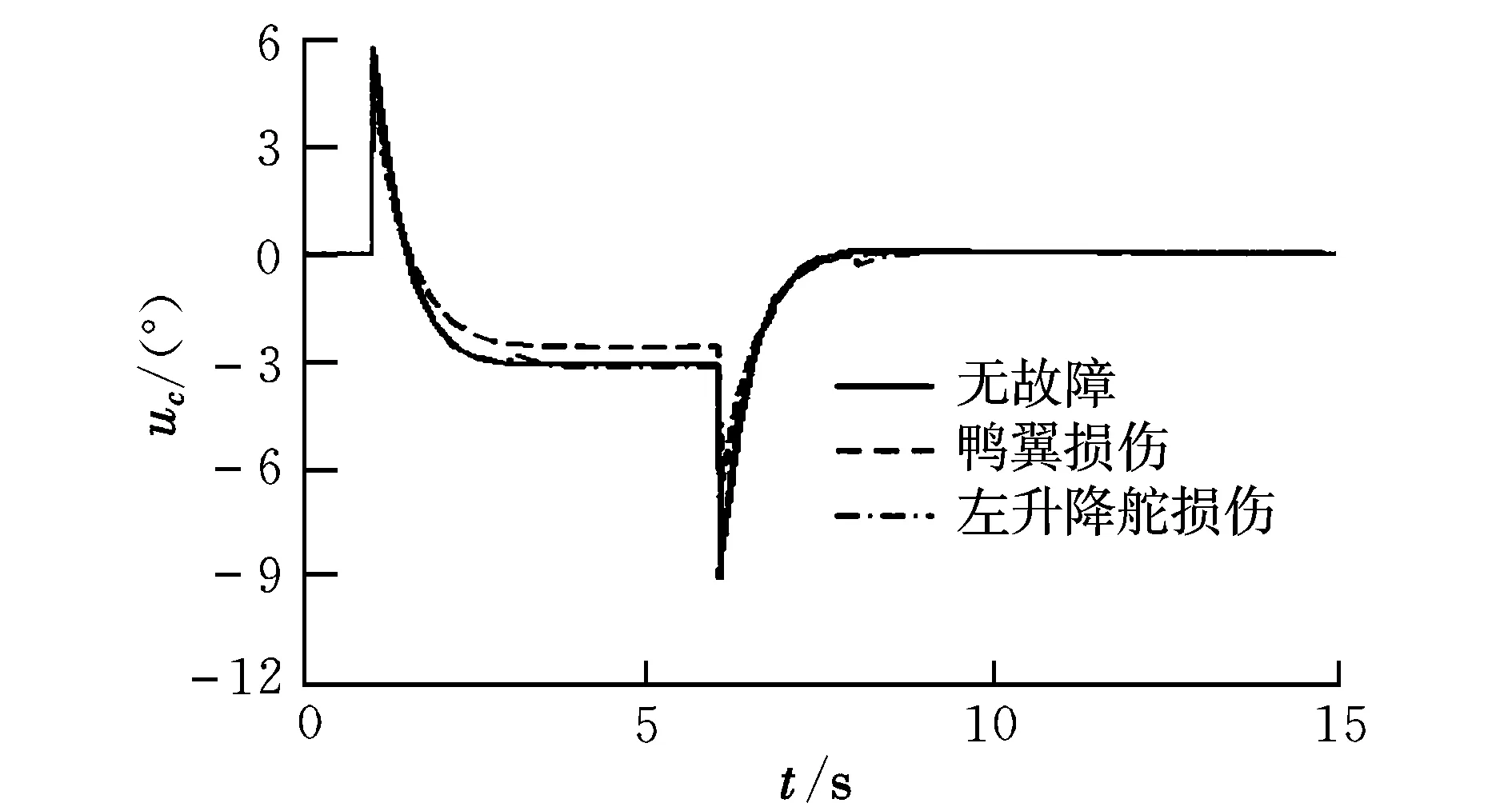
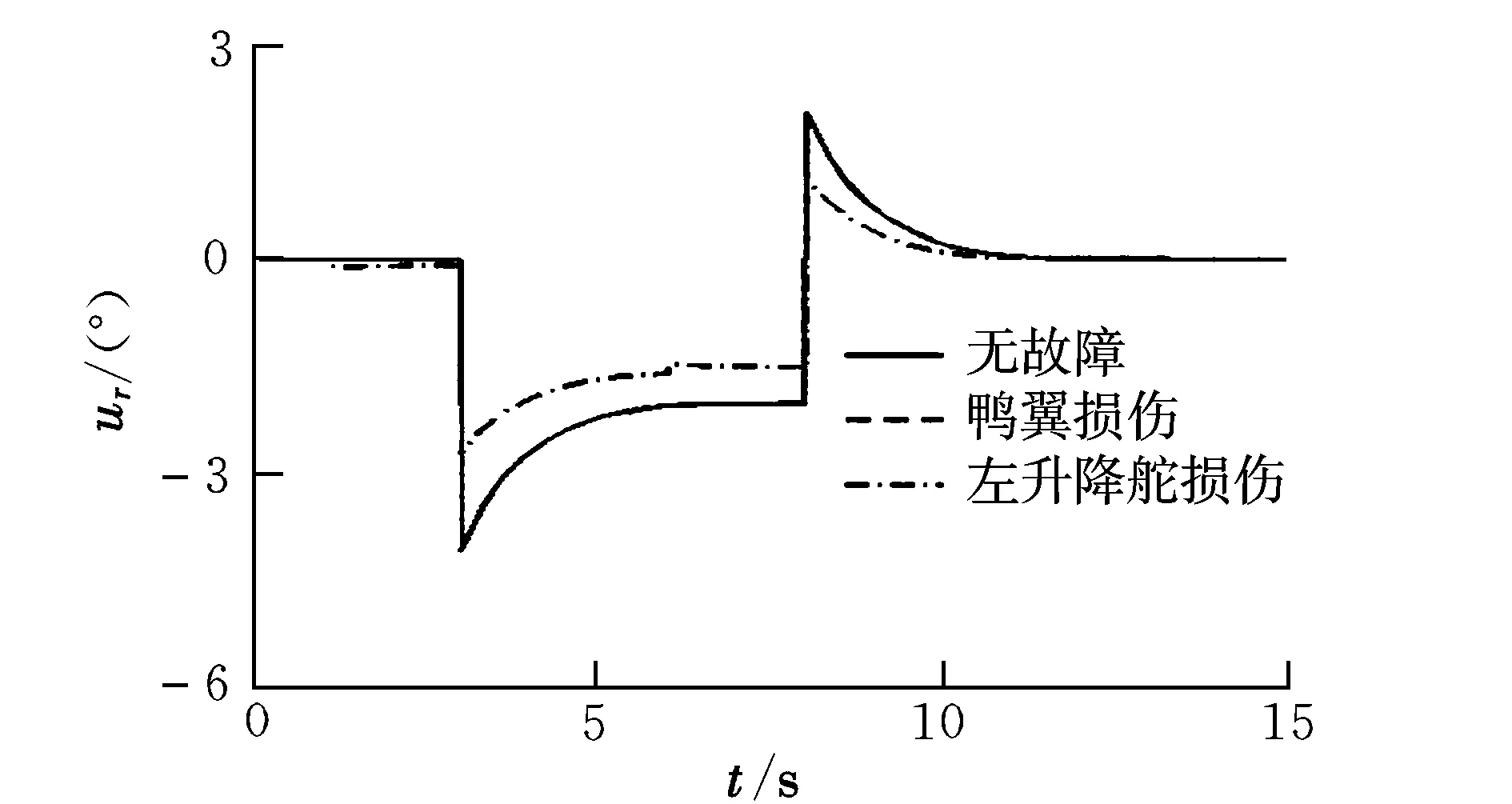
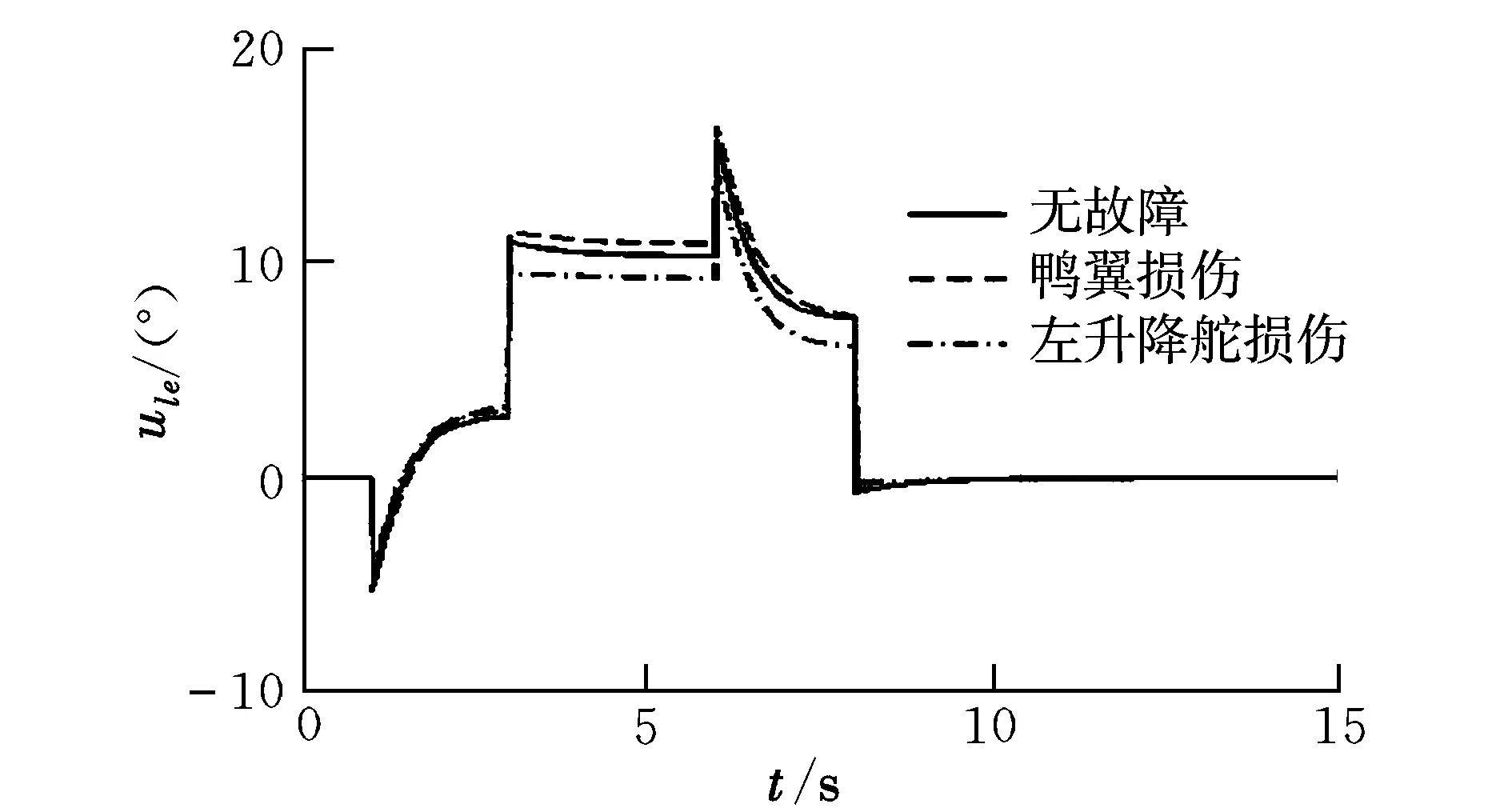
式中,u(t)为执行器输入指令;W=diag[w1,…,wm],为执行器故障矩阵,当wi=1时,表示相应的第i个执行器无故障;当0 将式(2)代入式(1)可以得到执行器故障情况下的线性化数学模型为: (3) 引入文献[7]的变换思想,可将B矩阵划分为: (4) 定义虚拟控制输入为: v(t)=B2u(t) (5) (6) 结合式(3)~式(6),可以将系统式(1)转化为具有层级结构的数学模型: (7) 其中: (8) 记 (9) 则包含执行器故障的系统转化为: (10) 进一步可知,当执行器无故障时,系统可写成: (11) 其中: (12) (13) 能够稳定。 2.1 积分滑模面的设计 根据最优二次型理论的相关结论[8],为保证控制器具备对给定指令的跟踪性能,针对系统式(11)可定义前馈增益矩阵为: Lr=C(BvF-A)-1Bv (14) 由此,给定跟踪的参考信号r(t),构建积分滑模面 {x∈Rn:σ(x,t)=Gx(t)-Gx(t0)- (15) 式中,σ(x,t)为切换函数;G∈Rl×n可以改善系统不确定性的影响,在此选取 G=B2(BTB)-1BT (16) 明显地,存在 于是对σ(x,t)=0求导可得: (17) (18) 将式(18)代入式(10)可得: Bw(GBw)-1Lrr(t) (19) 进一步可将式(19)转化为: Bw(GBw)-1Lrr(t) (20) 其中: (21) (22) 给定的跟踪指令r(t)必然有界,为此闭环积分滑模系统的稳定性取决于 (23) 设: (24) (25) (26) 则式(23)可写成: (27) (28) 根据小增益定理[12],如果 (29) 则系统是稳定的。因此,如果满足 ‖Φ(t)‖<γ1 (30) (31) 则对于任意执行器故障时,即满足0 γ1γ2<1 (32) 2.2 积分滑模控制律设计 将式(10)代入式(17)可得: (33) 为了构建稳定的积分滑模控制律,选取李雅普诺夫函数为: V(t)=(1/2)σT(t)σ(t) (34) 对V(t)求导数可得: (35) 下面分两种情况讨论: (1)当σ(t)=0时 (36) 从而系统稳定,且 (37) (2)当σ(t)≠0时,不妨假设 (38) 即系统渐近稳定。根据式(33)和式(38)可知: (39) 由此可得: (40) 综上可知,基于虚拟变量的积分滑模控制律为: (41) 进一步结合式(5)、式(6)、式(9)和式(40)可得过驱动执行器的控制律为: (42) 2.3 控制器增益设计 对于系统式(11),使闭环系统稳定的控制器增益F[8]可通过最优二次型设计实现。由于(A,Bv)可控,选择优化目标: (43) 式中,Q和R为对称正定矩阵。 由文献[12]可知,要使系统存在最优状态反馈控制器,当且仅当存在矩阵Y∈Rl×m和对称正定矩阵X∈Rn×n,使得 (44) X>0 (45) 成立,进而可知F=YX-1。 同时,对于闭环系统函数式(27),根据有界实引理[12],要使系统满足式(32)的小增益稳定性条件,当且仅当存在矩阵Y∈Rl×m和对称正定矩阵X∈Rn×n及常数γ,使得 (46) 成立。 综上,建立同时满足优化性和稳定性的线性矩阵不等式优化模型为: (47) 式中,α1>0,α2>0,为加权系数。 引入对称正定矩阵Z∈Rn×n,可将其转化为如下线性矩阵不等式凸优化模型: (48) 为了验证该方案的有效性,采用某多操纵面飞机[13]为对象进行研究。状态变量x=[α,β,p,q,r]T;控制量u=[uc,ure,ule,ur]T,分别表示鸭翼、右升降舵、左升降舵、方向舵的偏角;选择参考指令为r(t)=[α,β,p]T。在高度h=3 500 m,Ma=0.3的飞行状态下,过驱动飞行控制器模型式(1)的系数矩阵为: B= 在Matlab/Simulink环境下建立飞行控制系统仿真模型。选择参数为:Q=diag(15,15,1,3,10),R=diag(10,10,10)。求解凸优化模型式(48)可知,γ=4.941 7。进一步可以得到:γ1=0.169 8,γ2=0.949 6。显然满足γ1γ2<1。 假设在1~6 s对飞机施加8°的迎角指令,在3~8 s施加100 (°)/s的滚转角速率指令,侧滑角参考指令始终为0°。分别对操纵面健全、鸭翼故障及升降舵故障三种情形进行仿真。图1~图9为操纵面无故障、鸭翼控制效能损伤30%及左升降舵控制效能损伤20%的情形下,闭环系统和操纵面的响应过程。 图1 α响应曲线 图2 β响应曲线 图3 p响应曲线 图5 r响应曲线 图6 uc响应曲线 图7 ure响应曲线 图8 ur响应曲线 图9 ule响应曲线 由图1~图9可知,在操纵面健全的情况下,该方案可以基本无稳态误差地跟踪给定的参考指令,并且仅产生很小的侧滑角响应。 当鸭翼损伤30%时,该方案将控制律重新分配到左升降舵、右升降舵和方向舵,但降低鸭翼的控制指令,整体上操纵面偏转协调。在迎角、俯仰角速率控制上虽有所损失,但损失不大并且很快补偿到与无故障时相当的效能水平,表现出良好的跟踪性能和良好的容错能力。 当左升降舵损伤20%时,本文方案同样能够较好地实现左升降舵条件下的容错控制。尽管通过鸭翼、左右升降舵和方向舵的协调偏转实现了滚转控制缺失的补偿,但滚转角速率仍然出现了一定的损失,侧滑角也存在小量的补偿误差。总体来看,该方案基本能够实现左升降舵故障时的飞行控制,保证了系统的稳定性。 本文基于积分滑模控制方法,提出了一种容错飞行控制器设计方案,以解决过驱动飞行控制系统中故障执行器的协调分配问题。将积分滑模与控制律分配技术相结合,建立了层级飞行控制结构中的容错控制器凸优化模型,并利用线性矩阵不等式求解综合考虑优化性和稳定性的折中解,同时根据设计的李雅普诺夫函数证明了系统的渐近稳定性。以某多操纵面飞机为对象的仿真结果表明,该方法可综合考虑执行器完好和故障时的控制效能,能够在不改变控制器结构的情况下实现多操纵面容错飞行控制,保证了闭环系统的稳定性,具有较好的鲁棒性。 [1] 马建军,郑志强,胡德文. 包含执行器动力学的子空间预测动态控制分配方法[J]. 自动化学报,2010,36(1):130-138. [2] Ye Dan,Yang Guang-hong.Adaptive fault-tolerant tracking control against actuator faults with application to flight control[J].Transactions on Control Systems Technology,2006,14(11):1088-1095. [3] Zhang Y M,Suresh V S,Jiang B,et al.Reconfigurable control allocation against aircraft control effector failures[C]//16th IEEE International Conference on Control Applications.Singapore,2007:1197-1202. [4] Casavola A,Emanuele G.Adaptive fault tolerant actuator allocation for overactuated plants[C]//Proceedings of the 2007 American Control Conference.USA,2007:3985-3990. [5] Boskovic Jovan D,Nathan Knoebel,Raman K Mehra.An integrated approach to damage accommodation in flight control[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit. USA,2008:1-25. [6] Oppenheimer M W,Doman D B.Reconfigurable control design for the X-40A with in-flight simulation results[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Rhode Island,2004:1-9. [7] Alwi H,Edwards C.Fault tolerant control using sliding modes with on-line control allocation[J].Automatica,2008,44(4):1859-1866. [8] Ola Harkegard,Glad S T.Resolving actuator redundancy-optimal control vs control allocation[J].Automatica,2005,41(1):137-144. [9] 陈勇,董新民.多操纵面优化控制分配新方法[J].飞行力学,2009,27(2):72-76. [10] 陈杰,李志平,张国柱.不确定非线性系统的高阶滑模控制器设计[J].控制理论与应用,2010,27(5):563-569. [11] Johannes T,Johansen T A.Adaptive control allocation[J].Automatica,2008,44(11):2754-2765. [12] 俞立.鲁棒控制-线性矩阵不等式处理方法[M].北京:清华大学出版社,2002: 23-140. [13] Forssell L,Nilsson U.Admire the aero-data model in a research environment version 4.0 model description[R].Techical Report,Swedish Defence Agency (FOI),2005. Integralslidingmodefaulttolerantcontrolforover-actuatedvehicle BAO E-er-dun, WANG Xiao-ping, DONG Xin-min, CHEN Yong (Engineering Institute, Air Force Engineering University, Xi’ an 710038, China) To solve the coordination and assignment problem of over-actuatated flight control system for the actuator failure, a fault tolerant flight control method based on integral sliding mode is proposed.Through introducing virtual control concept, aircraft hierarchy structure control mathematical model is constructed in the case of the redundancy actuator failure. This paper utilizes the small gain theorem to derive the stable sufficient condition of the closed loop system and establishes the convex optimization model with optimal state feedback via using the LMI optimization simultaneously.By taking the integral switching function of sliding surface as a variable and selecting the Lyapunov energy function, the design of integral sliding mode controller with the asymptotic stability is proposed.Simulation results show that this method considers comprehensively the control performance of the actuator with health and failure, achieves fault tolerant for flight control with more control surfaces and has good robustness. over-actuated vehicle; tolerant control; control allocation; integral sliding mode 2011-05-11; 2011-09-21 鲍额尔顿(1984-),男(蒙古族),内蒙古阿盟人,硕士研究生,研究方向为故障诊断、控制重构。 V249.1 A 1002-0853(2012)01-0038-05 (编辑:姚妙慧)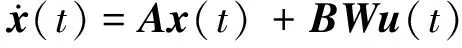
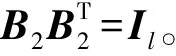
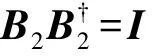
2 积分滑模控制律设计


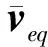
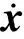
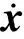
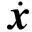

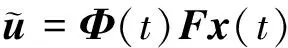
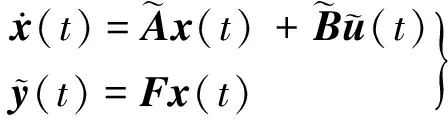
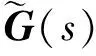
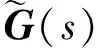
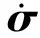


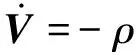


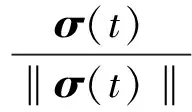
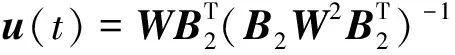
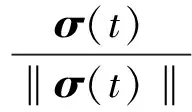
3 仿真验证




4 结束语

