地空导弹三点法三维运动学弹道建模与仿真
张大元, 赵玉芹, 雷虎民, 吴一鸣
(空军工程大学 导弹学院, 陕西 三原 713800)
地空导弹三点法三维运动学弹道建模与仿真
张大元, 赵玉芹, 雷虎民, 吴一鸣
(空军工程大学 导弹学院, 陕西 三原 713800)
针对三点法三维运动学弹道仿真问题,建立了两种仿真模型。第一种模型采用数值积分算法求解三点法运动学方程组,求解过程较为复杂;第二种模型利用三维空间相关几何知识,将求解三点法三维运动学弹道的图解法转化为求解一元二次方程的问题,使求解过程简单直观。最后,对两种模型进行了仿真,并将其应用到地空导弹制导控制系统的仿真研究中,将理想弹道与控制弹道进行了对比。结果表明,两个模型均解决了一般情形下三点法三维运动学弹道求解的问题,为三点法三维制导律以及弹道特性研究提供了一种方法。
地空导弹; 三点法; 三维运动学弹道; 仿真
引言
三点法因实现较为简单,一直是采用遥控制导体制的地空导弹常用的导引方法,绘制其三维运动学弹道不仅是研究该导引规律以及弹道特性的需要,而且在地空导弹全弹道仿真中,需要绘制理想运动学弹道来为仿真弹道提供参考,是进行制导控制系统仿真的一个环节。
针对三点法的运动学弹道,许多有关导弹飞行力学的文献中都有描述,也有许多学者研究了三点法弹道的绘制方法,如文献[1]给出了在铅垂平面内三点法运动学方程组,并详细描述了三点法运动学弹道的图解法;文献[2]对三点法原理进行了详细的分析,并给出了铅垂平面内采用三点法抗击匀速直线运动目标情形下,运动学弹道的解析方法;文献[3]也给出了垂直平面内目标匀速直线运动情形下的三点法运动学弹道的解析解。但是,即使在铅垂平面内,当目标机动时,运动学弹道的求解就比较困难了,更不用说三维空间中目标机动的情形。所以,研究三点法三维空间拦截机动目标的运动学弹道是很有意义的。
本文从求解导弹三维运动学方程组入手,建立了两种模型,第一种是适用于三维运动空间和目标机动情形的三点法运动学弹道仿真模型;第二种是参考三点法图解原理,结合三维空间相关几何知识,使弹道求解过程简单、直观。
1 参考坐标系
1.1 测量坐标系
研究地空导弹三点法导引规律,通常采用测量坐标系Oxjyjzj,该坐标系原点选在地面制导站上,Oxj轴在制导站和目标的连线上,指向目标为正;Oyj轴在通过Oxj轴的铅垂平面内,垂直于Oxj轴向上为正;Ozj轴按右手定则确定。测量坐标系可由地面坐标系经由两次旋转得到,如图1所示。图中,ε为高低角,β为方位角。
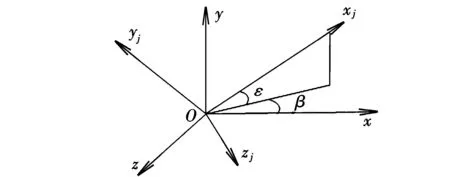
图1 测量坐标系和地面坐标系
测量坐标系相对地面坐标系的转换矩阵为:
(1)
1.2 弹道坐标系
弹道坐标系Oxcyczc,该坐标系原点选在飞行器质心上,Oxc轴与飞行器速度矢量重合,向前为正;Oyc轴在通过Oxc轴的铅垂平面内,垂直于Oxc轴向上为正;Ozc轴按右手定则确定。弹道坐标系可由地面坐标系经由两次旋转得到,如图2所示。图中,θ为弹道倾角,φc为弹道偏角。
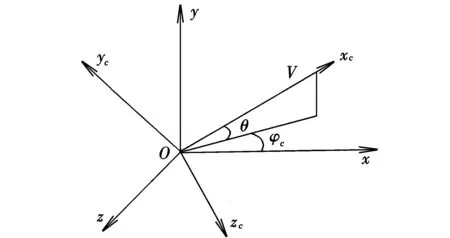
图2 弹道坐标系和地面坐标系
弹道坐标系相对地面坐标系的转换矩阵为:
(2)
2 三点法导引规律运动学方程组的建立
所谓三点法导引规律是指:导弹在攻击目标的飞行过程中,使导弹、目标和制导站始终在一条直线上。其导引原理如图3所示。图中,R,Rm代表导弹和目标的斜距。

图3 三点法理想导引示意图
根据运动学规律,在测量坐标系中,制导站与导弹之间的运动学关系为:
(3)
式中,Vxj,Vyj,Vzj分别为导弹运动速度在测量坐标系沿各坐标轴的分量。
下面分别求解式(3)所需的3个速度分量。首先,将导弹速度从弹道坐标系分解到地面坐标系,依据式(2),得:
(4)
式中,V为导弹速度;Vxd,Vyd,Vzd为导弹速度在地面坐标系各坐标轴的分量。
再利用式(1),得:
(5)
化简式(4)、式(5)得:
(6)
这样,由式(3)和式(6)可得导弹相对制导站的运动学方程为:
(7)
同理可求得:
(8)
式中,Vmxj,Vmyj,Vmzj分别为目标运动速度在测量坐标系沿各坐标轴的分量;Vm为导弹速度;θm,φcm分别为目标的弹道倾角和弹道偏角;βm,εm分别为目标的偏航角和高低角。
同式(7),可求得目标相对于制导站的运动规律为:
(9)
这样,式(7)和式(9)就构成了求解三点法运动学弹道所需的6个方程。为求解该方程,要求的已知量包括目标运动参数(Vm,θm,φcm,εm,βm)和导弹速度V,另外,还需要三点法的导引方程:
(10)
这样,方程组(7)、(9)、(10)共8个方程,8个未知数,方程组可以求解。
3 仿真模型
3.1 仿真模型1
仿真模型1采用四阶龙格库塔法求解由式(7)、式(9)和式(10)构成的运动方程组,由于导弹的弹道偏角和倾角不是显式表达的,故需要转化求解。
若是导弹始终按照三点法的导引方程飞行,则有:
(11)
这样,就可以将式(7)和式(9)中的第二、第三个方程联立:
(12)

(13)
考虑到

中没有直接使用弹道倾角和弹道偏角的值,所以没有必要求解θ和φc的具体值,只要将其正弦或余弦值作为一个整体求解即可。
将式(13)代入式(12)得:
(14)
为使方程简洁,作以下换元:
(15)
由式(14)和式(15)可得:
(16)
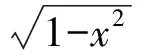
(17)
化简式(17),得:
x2-2mpx-(n2-n2q2-p2)=0
(18)
求解该式,x即为所得正根,将x代入式(16)第一个方程,可得y值,将x,y代入

(19)

采用仿真模型1进行仿真验证的流程如下:
(1)给出目标运动规律(包括初始位置Rm0,εm0,βm0,弹道倾角及偏角变化规律,目标速度Vm);导弹初始位置R0,ε0,β0;导弹速度V;
(2)积分式(9),求解目标位置参数Rm,εm,βm;
(3)求解式(18),利用其结果积分式(19),得到导弹斜距R;
(4)根据导引规律,导弹高低角和方位角与目标一致,即ε=εm,β=βm;
3.2 仿真模型2
三点法导引弹道用图解法更为直观方便,但是图解结果不便于转化为坐标值,仿真模型2把图解法转化为一元二次方程。
参照图3,设导弹初始位置为D(xd1,yd1,zd1),目标初始位置为M(xm1,ym1,zm1),经过时间Δt,目标飞行至M′(xm2,ym2,zm2),导弹在服从导引律的情况下,应该飞行至D′(xd2,yd2,zd2),假设在时间间隔较小的情况下,导弹速度保持匀速,该导弹新坐标即为所求值。
由导引规律知,导弹新坐标满足以下条件:
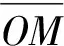


由条件(1)和(2)可以列写等价方程:
(20)
令
(21)
将式(21)代入式(20),得:
(22)
求解该方程,得k值。
依据式(20)求得导弹坐标:
(23)
若是有两个k值,则分别求解导弹坐标,然后选择导弹yd2满足yd2≥yd1的k值,这是因为地空导弹一般是向上飞的。
采用仿真模型2进行仿真的步骤如下:
(1)给出导弹和目标初始位置D(xd1,yd1,zd1),M(xm1,ym1,zm1);导弹和目标速度V,Vm;仿真步长Δt;
(2)求解目标坐标M′(xm2,ym2,zm2);
(3)依据式(20)~ 式(23)求解导弹的坐标D′(xd2,yd2,zd2);
4 仿真算例
假设某地空导弹按照三点法拦截作等高圆弧形机动的目标。目标初始机动过载为5,速度为700 m/s,位置M(18 373,15 000,-18 373) m,开始机动时间为0 s。导弹初始速度为800 m/s,位置D(0,0,0) m。
采用Matlab语言对两个模型进行了仿真,分别绘制了两种模型在拦截同一机动目标时的理想弹道曲线,如图4所示。

图4 三点法三维运动学弹道
最后,将所设计的理想运动学弹道求解模型应用于全弹道仿真软件中,作为理想弹道与控制弹道进行比较。在仿真中,导弹速度是由导弹动力学方程求解得到的控制速度,从而说明当导弹速度为变量时,两个仿真模型依然适用。仿真结果如图5所示。由图5可知,实际弹道总是围绕理想运动学弹道运动的[4-5],所以理想运动学弹道可以用来检验控制弹道的准确程度,从而检验导弹制导控制系统的精度。

图5 控制弹道与理想弹道的比较
5 结束语
通过以上仿真分析以及模型最后的使用效果可知,文中建立的地空导弹三点法三维运动学弹道的两种仿真模型都是有效的,模型精度都比较高,但在实际的仿真中,常采用数值积分的方法,可是在理解三点法的原理时,图解法更容易让人接受,所以两种模型各有优劣。
当今,仍有很大一部分新型地空导弹武器采用了三点法这种实现简单、精度较高的导引方法,本文为三点法三维导引规律以及三点法的应用研究提供了一种有力的工具。
[1] 雷虎民.导弹制导与控制原理[M].北京:国防工业出版社,2009:82-89.
[2] 周慧钟,李忠应,王瑾.有翼导弹飞行动力学[M].北京:北京航空航天大学出版社,1987.
[3] 朱卫兵,张耀良.战术导弹三点法遥控制导弹道方程的解析解[J].弹箭与制导学报,2006,26(1):245-247.
[4] 邓方林,黄先祥.弹道导弹六自由度仿真决策系统设计与研制[J].系统仿真学报,2004,16(2):186-189.
[5] Curtis P Mracek,Ridgely D Brett.Optimal control solution for dual(tail and canard)controlled missiles[R].AIAA-2006-6569,2006.
Modelingandsimulatingonkinematictrajectoryofground-to-airmissilecontroledbythree-pointmethod
ZHANG Da-yuan, ZHAO Yu-qin, LEI Hu-min, WU Yi-ming
(Missile Institute, Air Force Engineering University, Sanyuan 713800, China)
Two new simulation models are established for the simulation of three-dimensional kinematic trajectory of ground-to-air missile controled by a three-point method. The first model is to solve the equation of the three-point method by integral method, which is complex; The second model translates the geometrical method into a unitary-quadratic equation, which is simple and intuitional. At last, the two models are simulated and applied in the research of the guidance and control sysytem for ground-to-air missile, the ideal trajectory is contrasted with the real one. The results show that both of the models can solve the problem of drawing three-dimensional kinematic trajectory of the three-point method, as a result, three-dimensional guidance-law of the three-point method and characters of the trajectory can be researched easily.
ground-to-air missile; three-point method; three-dimensional kinematic trajectory; simulation
2011-04-06;
2011-08-23
航空科学基金资助(20090196005;20100196002)
张大元(1987-),男,山东滕州人,硕士,主要从事导弹控制系统研究;
赵玉芹(1961-),男,山东汶上人,副教授,硕士生导师,主要从事防空导弹引信技术研究。
TJ762.13; TJ765
A
1002-0853(2012)01-0057-04
(编辑:姚妙慧)

