基于微分进化算法的二自由度PID控制器参数优化

刘棕成, 董新民, 陈勇

(空军工程大学 工程学院, 陕西 西安 710038)

基于微分进化算法的二自由度PID控制器参数优化

刘棕成, 董新民, 陈勇

(空军工程大学 工程学院, 陕西 西安 710038)

针对二自由度PID控制器参数多、调节困难等问题,提出了一种基于微分进化算法参数调节优化方法。证明了微分进化算法能够收敛到平稳点,并具有概率全局收敛性。研究了二自由度PID控制器参数与抑制特性、跟踪特性的关系,并将微分算法与遗传算法、粒子群算法的参数优化结果进行了比较。仿真验证表明,微分算法能够更好地实现二自由度PID控制器参数的调节,具有优异的跟踪特性和抑制特性。

微分进化算法; 收敛性; 二自由度PID控制器; 参数优化

引言

在现代飞行控制领域中,被控系统的非线性、不确定性和复杂性使得传统的一自由度PID控制器已经越来越难以满足系统对控制性能的要求,而二自由度PID控制器因具有良好的控制性能已越来越受到人们的重视。但是,二自由度PID控制器的待调整参数较多,控制器参数需经过反复细致的调整才能实现最优化,工作量大,已经成为限制其在控制领域应用的瓶颈。

近年来,先进智能计算科学的发展带动了诸如遗传算法(GA)[1]、粒子群算法(PSO)[2]、微分进化算法(DE)[3]等智能优化算法的迅速崛起。此类算法原理简单,收敛性好,在多目标优化[4]、非线性函数优化等方面表现出优异的性能,尤其在PID参数整定中展现出传统优化算法无法比拟的优势[5]。但是,若系统需多个参数需要同步优化,遗传算法存在早熟、参数依赖性强的缺点[6];粒子群算法容易陷入局部最优,限制了其应用;而微分进化算法以其在多参数非线性优化方面的优越性能在1996年日本召开的第一届国际进化优化计算竞赛(ICEO)中取得了优异成绩,受到了越来越多的重视,在约束优化计算、智能控制器优化设计、滤波器设计等方面得到了广泛的应用。

本文利用微分算法搜索能力强、鲁棒性好、控制参数少等特点,提出了一种基于微分进化算法的二自由度PID控制器参数优化方法。通过与遗传算法和粒子群算法仿真对比,进一步验证了微分算法对二自由度PID参数优化的优越性。

1 微分进化算法分析与研究

1.1 算法的数学描述

(1)初始化:在解空间随机选择初始种群X(0),设置变异常数F,交叉概率Pc,种群规模N。

(2)变异:随机选取r1,r2,r3∈rand(1,n),且i≠r1≠r2≠r3。则:

(1)

(3)交叉:

(2)

(4)选择:

(3)

1.2 算法的收敛性分析

收敛性是算法的一个重要性能,所以有必要对算法的收敛性进行分析。下面讨论连续变量函数优化时微分算法的收敛性。

引理1[7]:若函数f(x)是单调递减,并且有下界,那么它一定收敛。

(1)单调性

微分算法是根据贪婪准则选取下一代个体的,从而对于任意进化代数t都有:

(4)

(2)有界性

(5)

1.3 种群进化趋势分析

前面已证明微分算法是收敛的。下面分析随着t的增加,算法的适应度值链是不断地趋于极值点的。

设:

(6)

图1 种群变化趋势图

S={X(t)||f(X(t))-f*|<ε}

(7)

2 二自由度PID控制器参数优化

在反馈控制系统中,若有数种传递函数,对其中两个传函可以独立设定的系统就被称为二自由度控制系统。比较常用的二自由度PID控制方式有前馈型、设定值滤波型和不完全微分型。本文只对设定值滤波型二自由度PID控制器的参数优化问题进行讨论和研究。

2.1 设定值二自由度PID控制器

设定值滤波型二自由度PID控制系统如图2所示。

图2 设定值滤波型二自由度PID控制系统框图

响应表达式为:

(8)

其中:

(9)

(10)

(11)

(12)

0<α,β,γ<1

(13)

由C(s)和M(s)完成干扰的最佳抑制,C(s)和H(s)实现设定跟踪最佳。控制器中有Kp,Ti,Td,α,β和γ共6个参数。

2.2 控制器参数研究

(1)抑制特性影响分析

由式(8)可以得到,干扰通道传递函数为:

(14)

Φdy(s)的闭环特征方程为:

Δ(s)=[C(s)+M(s)]G(s)+1

(15)

假定Td≫0.1Td,则系统开环传递函数为:

(16)

由式(16)可以看出,C(s)和M(s)使系统新增了两个开环零点和一个固定在原点位置的开环极点,且两零点仅当Ti和Td变化时其位置移动。通常,Td增大时它们会远离虚轴;Ti增大,会靠近实轴。它们可以通过Ti和Td配置在S平面任意位置,所以只要Kp,Ti和Td的取值合适完全能使抑制特性达到理想效果。

(2)跟踪特性影响分析

控制跟踪通道的传递函数为:

(17)

从式(17)可以看出,跟踪控制回路的闭环特征方程与抑制回路的相同,α,β和γ只影响闭环系统增加的零点位置。而闭环零点会影响各模态的输出幅值,从而抑制某些不利于跟踪模态的输出。

通过以上分析,可以得到二自由度PID控制原理如图3所示。

图3 二自由度PID控制原理图

抑制回路有Kp,Ti和Td共3个参数,控制跟踪回路包含所有控制器参数,而Kp,Ti和Td主要用来实现抑制最佳,α,β和γ用来实现跟踪最佳。所以,二自由度PID控制方式能够同时实现很好地跟踪和抑制功能,但参数变化对系统性能的影响规律是复杂的,需要用算法来进行寻优。

2.3 参数寻优方案设计

以某Ⅰ型三阶最小相位系统为被控对象,即:

(18)

利用微分算法对二自由度PID参数进行优化,令待整定的参数集(Kp,Ti,Td,α,β,γ)作为寻优空间的种群个体位置。考虑到ITAE最优控制系统具有优良的系统响应和选择性,选取ITAE性能指标作为算法的适应度函数。通过微分算法的迭代,找出一组参数(Kp,Ti,Td,α,β,γ),使得系统响应的ITAE值J达到最小。同样,用标准遗传算法、粒子群算法[8]进行相同的寻优操作,也能分别得到一组参数。

3 仿真结果分析

根据第2.3节所设计的参数寻优方案,分别对算法的控制参数设置进行控制器参数寻优。

(1)遗传算法:交叉概率Pc=0.5,变异概率Pm=0.3,最大迭代次数Gmax=80,种群规模N=60。

(2)粒子群算法:设定学习因子c1=c2=2,种群粒子数n=60,最大迭代次数Gmax=80,惯性权值为W=0.5。

(3)微分进化算法:交叉概率Pc=0.5,变异常数F=0.7,最大迭代次数Gmax=80,种群规模N=60。

3.1 跟踪特性分析

各算法寻优过程如图4所示,得到的寻优结果如表1所示。

表1 各算法参数寻优结果

将上述所得控制器参数优化结果分别进行仿真验证:令图2所示的控制系统的输入R(s)=1/s,D(s)=0,可以得到系统时域内的输出响应如图5所示。

由图4可以看出,微分算法收敛速度明显较快,搜索能力更强,得到的性能指标值更优。由图5可知,与遗传算法和粒子群算法相比,经微分算法进行参数优化的控制系统跟踪特性有明显的优势,上升时间短,而且几乎没有超调量。

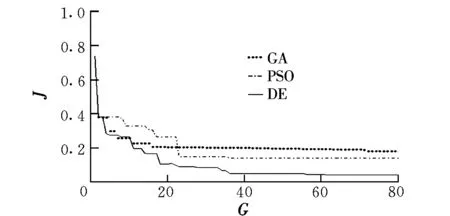
图4 目标函数寻优过程图

图5 二自由度PID控制系统阶跃响应图

3.2 抗干扰性分析

二自由度PID控制器能使控制系统保持良好的跟踪特性,同时又具有较优的抗干扰特性,这使得其优于常规控制器。令干扰信号D(s)为白噪声,输入端为零,对优化后控制系统的抑制性能进行仿真分析,仿真结果如图6所示。

由仿真结果可以看出,微分算法优化后的二自由度PID控制器相对于其它两种算法抗干扰特性更好,噪声干扰对其的影响明显较小。

4 结束语

本文对微分进化算法收敛特性进行了分析,将算法应用于二自由度PID控制器参数优化,并与传统算法的优化结果进行了对比。从仿真结果来看,相比于遗传算法和量子粒子群,微分算法优化后的控制器在动态性能和稳态精度上都有明显优势,抗干扰性更好。而且算法原理简单,搜索能力很强,是一种可以应用于工业过程控制的优良方法。针对二自由度PID控制器的特点,怎样设置更合适的目标函数以获得最优的性能将成为下一步研究的重点内容。

[1] 李敏强,寇纪淞,林丹,等.遗传算法基本理论与应用[M].北京:科学出版社,2002.

[2] Cristian I,Trelea C.The particle swarm optimization algorithm:convergence analysis and parameter selection[J].Information Processing Letters,2003,83(6):317-325.

[3] Rainer S,Price K.Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):341-359.

[4] Bingul Z,Sekmen A,Zein-Sabatto S.Evolutionary approach to multi-objective problems using adaptive algorithms[C]//Proceedings of the IEEE International Conference on Systems,Man and Cybernetics.Piscataway,2000:1923-1927.

[5] Astrom K J,Hagglund T.The future of PID control [J].Control Engineering Practice,2001,9(4):1163-1175.

[6] 王小平,曹立明.遗传算法理论、应用与软件实现[M].西安:西安交通大学出版社,2002.

[7] 龚怀云,寿纪麟,王景森,等.应用泛函分析[M].西安:西安交通大学出版社,1995.

[8] 杨帆,胡春平,颜学峰.基于蚁群系统的参数自适应粒子群算法及其应用[J].控制理论与应用,2010,27(11):1479-1488.

Optimizationof2DfreedomPIDcontrollerparametersbasedonDE

LIU Zong-cheng, DONG Xin-min, CHEN Yong

(Engineering Institute, Air Force Engineering University, Xi’an 710038, China)

With regard to the parameter regulation problem with 2D freedom PID controllers which have multiple parameters, a parameter regulation and optimization method is put forward based on differential evolution(DE) algorithm, which can converge to the equilibrium point with global convergence in probability.The relation between 2D freedom PID controller parameters and the suppression and tracking characteristics is studied,and parameter optimization results using the DE algorithm are compared with those using the genetic algorithm and the PSO algorithm respectively.Simulation shows that the DE algorithm can regulate 2D freedom PID controllers very well with excellent tracking and suppression characteristics.

differential evolution algorithm; convergence; 2D freedom PID controller; parameter optimization

2011-06-29;

2011-12-16

刘棕成(1987-)，男，湖南衡阳人，硕士研究生，研究方向为控制理论与控制工程。

V249.1; TP273

A

1002-0853(2012)02-0139-04

(编辑：王育林)