无刷直流电动机混沌系统的滑模变结构控制

刘 浩，马草原，陈帝伊

(1中国矿业大学，江苏徐州 221116;2西北农林科技大学，陕西杨陵 712100)

0 引 言

永磁无刷直流电动机作为现代高性能调速电机，调速性能优越，鉴于无碳刷和换向器的结构特殊性，可设计成密闭结构电机，应用在多种特殊场合，如煤矿中应用于无轨电车的防爆永磁无刷直流电动机［1］以及矿山特种车辆电动转向系统EPS中的助力电机［2］。近年来，随着新型电机、机器人、功率开关器件以及航天航空技术等非线性学科的迅速发展，滑模变结构控制理论的研究成果［3－4］日益增多;同时，各种智能控制思想在滑模控制系统中的嵌入结合，也已成功应用在机器人系统［5－6］、航天器［7］以及电力系统［8］中;滑模变结构控制在混沌系统控制的应用［11－13］也已取得不少研究成果。目前，如何进一步消除控制抖振和展开工程实际应用是该方向待以深入的研究课题。本文以无刷直流电动机混沌数学模型为研究对象，提出了一种可以将无刷直流电动机混沌系统控制到任意目标的动态滑模变结构控制，并提出一种改进型无抖振的动态滑模变结构控制，提高了控制品质，理论研究和实验仿真证实了两种控制策略的有效性。

1 对象描述

无刷直流电动机作为一个典型的非线性动力学系统，当特性参数发生漂移时，电机则以转矩与转速的间歇振荡、控制性能不稳定、不规则电磁噪声等多种运行方式发生混沌现象，考虑到存在外界干扰和建模的不精确性，构造无刷直流电动机混沌控制系统［10］无量纲数学模型如下:

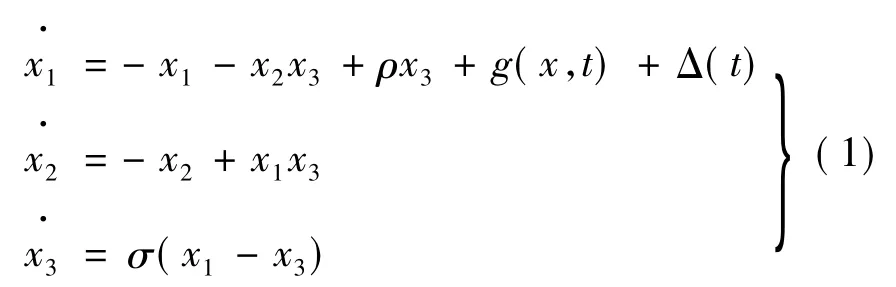
式中:x1、x2、x3反映了无刷直流电动机直轴电流、交轴电流、转速性质，g(x，t)和Δ(t)是混沌系统的不确定时变项和外部干扰项:

当 ρ=20.5、σ =4.5 时，此时的无刷直流电动机处于混沌运行状态，系统的混沌吸引子和系统状态变量的时间历程如图1、图2所示，此时自治系统的三个平衡点为 F0:(0，0，0)，F±:( ±4.416，19.5，±4.416)。

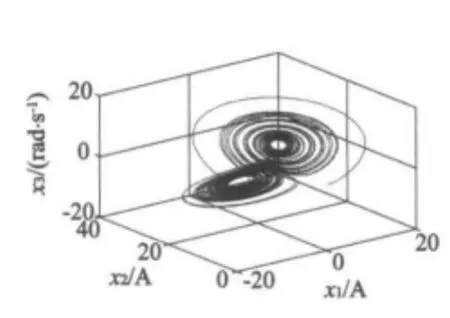
图1 BLDCM混沌系统相图

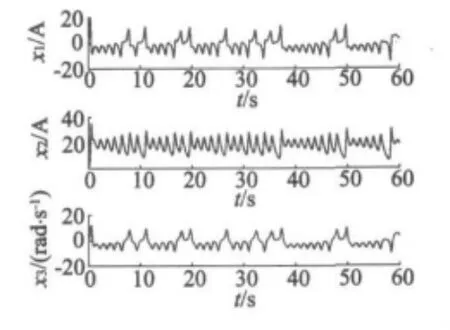
图2 状态变量时序图

2 动态滑模变结构控制研究

2.1 控制器研究

给出无刷直流电动机系统混沌的控制系统:

并设计式(3)的增广系统如下:

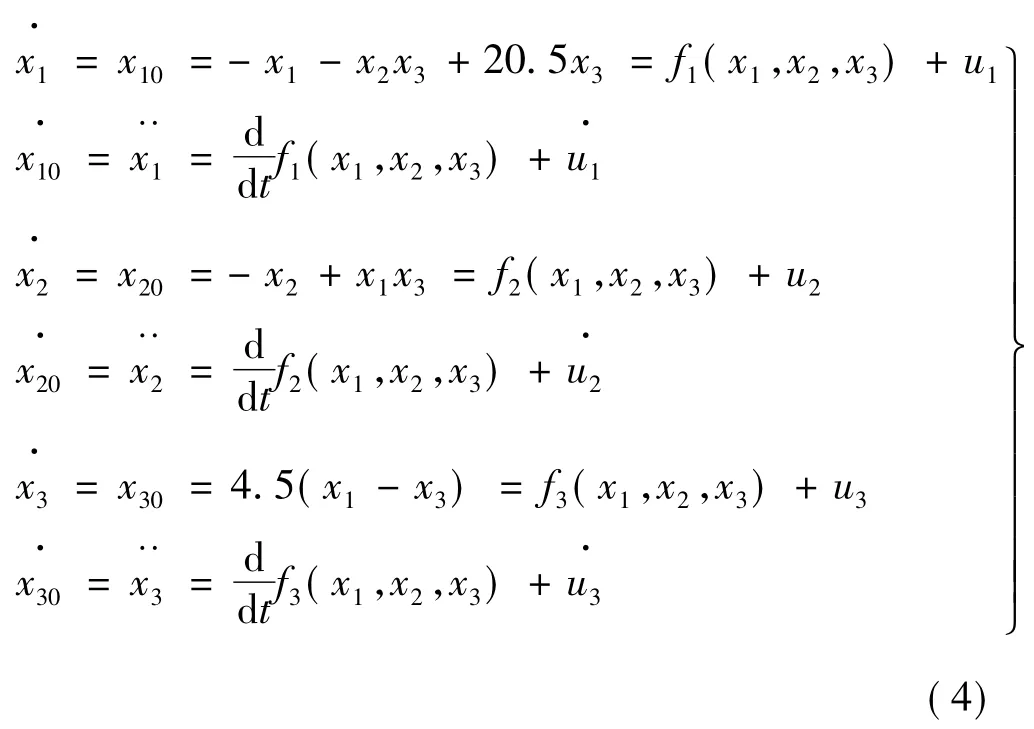
定义系统输出误差并设置混沌系统控制目标(x1d，x2d，x3d):

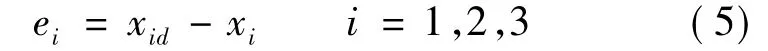
理论上为消除抖振，定义时变的动态比例积分滑模面:

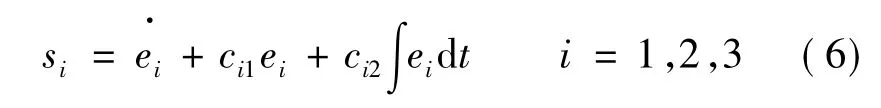
当系统运动于滑模态时，需满足:

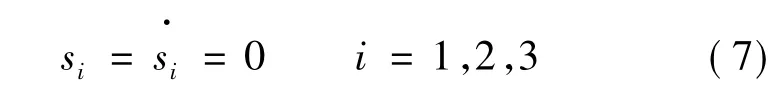
控制律采用等速趋近律:

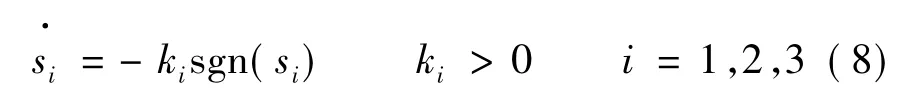
为满足滑模控制条件，设计控制策略:

其中符号函数定义如下:

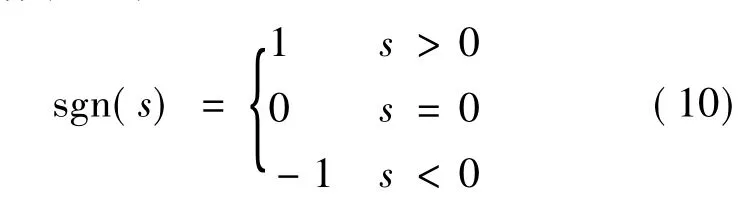
定理:若 k1、k2、k3为常数，且满足 k1＞0、k2＞0、k3＞0，则式(9)可使式(1)在有限时间内达到滑动模态S=0。

定理表明，通过施加合适的控制信号u1、u2、u3，将系统引导至期望轨道，式(9)可以将处于混沌运行状态的式(1)镇定到特定目标，且具有良好的鲁棒性。

2.2 数值仿真研究

本文提出的滑模控制器是基于无刷直流电动机无量纲数学设计的，故在MATLAB仿真实验中不提供部分变量单位，旨在讨论混沌控制器的控制和优化的有效性。以无刷直流电动机自治系统的非零平衡点为控制目标，即(x1d，x2d，x3d)=(4.416，19.5，4.416)。系统状态变量初值为(0.1，0.1，0.1)，控制器中各参数取值如下:根据定理1和仿真效果，不妨取 k1=k2=k3=1，c11=c12=5，c21=c22=5，c31=c32=5，仿真步长取0.0002 s，首先让系统在混沌状态下自由演化，控制器在第5 s加入。数值仿真结果如图3～图6所示。

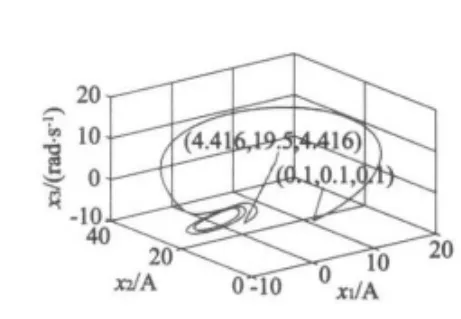
图3 控制到期望目标的系统相图

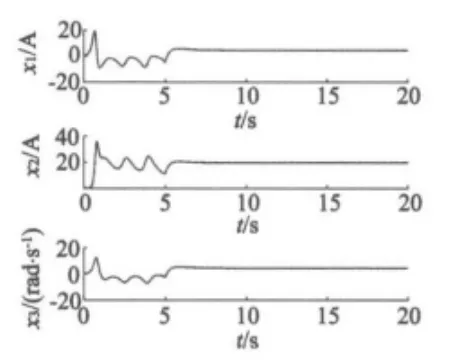
图4 状态变量时序图

图5 滑模面时序图

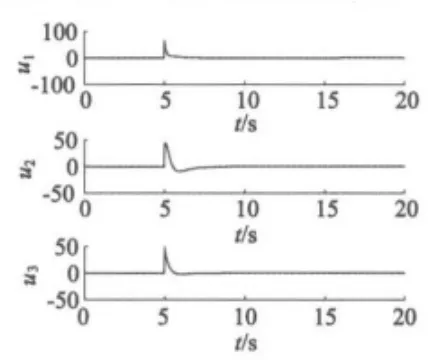
图6 控制器信号

由图3和图4可以看出，在混沌自由演化的第5 s时加入控制器，系统经过3 s左右的调节时间即到达控制目标。由图4和图5可以看出，滑动模量均能很好地跟踪预设滑模面，很快就到达滑模面附近很小的邻域内，控制器也很快到达稳定输出，混沌很快被消除，系统到达预设稳定状态，理论分析和仿真研究证实了动态滑模变结构控制应用在BLDCM混沌系统中的控制有效性。

3 改进型动态滑模变结构控制研究

含有积分的滑模面理论上可消除抖振，但根据上文仿真结果的滑模面局部放大图(图7)可以看出，虽然滑模控制达到了很好的控制效果，但是抖振的问题仍没有解决。因此本文通过改进趋近律和控制器结构，设计一种改进型滑模变结构控制算法，消除控制抖振现象。

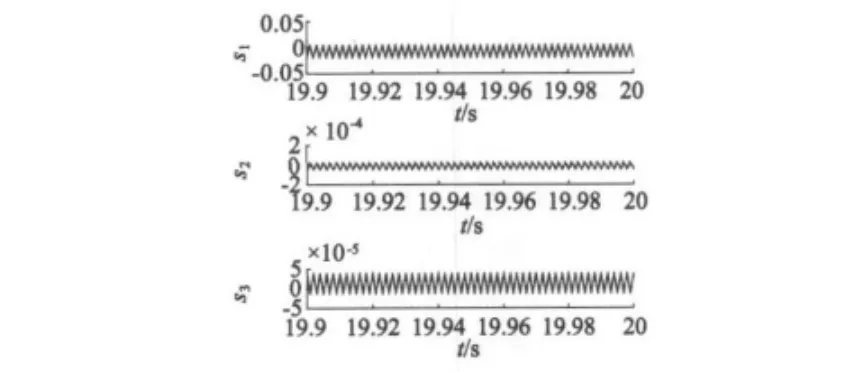
图7 滑模面局部放大图

3.1 控制器研究

控制抖振是滑模变结构控制的主要缺陷之一，目前在消除抖振方面主要的研究成果有两个方面［14］，一是以连续近似的方式趋近控制器的理想切换，但是该方法降低了控制器的抗干扰性;二是优化至切换面的到达速率，此种方法可尽量保留滑模变结构控制器的优良特性。

本文为了优化到达速率，使滑模量渐进跟踪滑模面，采用改进的自适应律和改进的控制律，通过饱和函数代替符号函数，指数趋近律代替等速趋近律，设计控制策略如下:

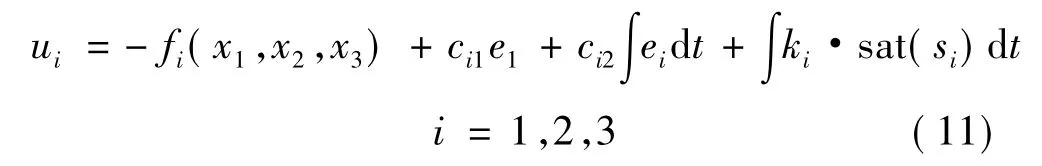
控制律中的参数k采用自适应律:

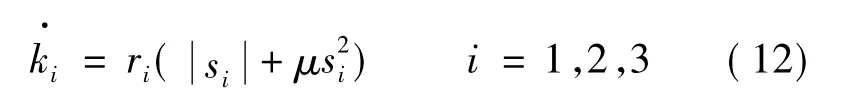
饱和函数sat(si)形式如下:

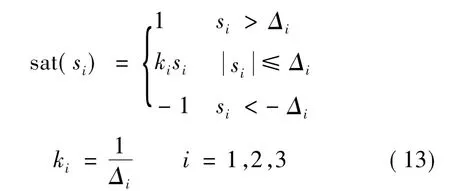
考虑到控制的快速性和稳定性，选择合适的参数Δi(i=1，2，3)以产生实用性强的饱和函数。从式(13)可以看出，s比较小时，饱和函数比符号函数有更细致的表现。而滑模最终的抖振正是发生在s=0附近很小的邻域内。因此，配合参数Δi合适的选取，饱和函数能取得削弱抖振的效果。

3.2 数值仿真研究

本文对所提出的抖振抑制方案进行了仿真实验验证。以(4.416，19.5，4.416)作为式(1)的控制目标，取系统状态变量初值为(0.1，0.1，0.1)，控制器式(11)中各参数取值如下:Δ1=Δ2=Δ3=0.01，c11=6，c12=1，c21=6，c22=1，c31=，6，c32=1，进行时长20 s的数值仿真实验，设置仿真步长0.002 s。

混沌系统在t=5 s时投入控制器，运行相图如图8所示，此时系统中的混沌现象被消除并渐进稳定在其平衡点处。图9为改进型滑模面的局部放大图，对比图7和图9可见，改进型动态滑模面波形光滑，减缓了向目标轨道的趋近过程，在10－4数量级以内控制的抖振现象已消除，量化指标参考如表1所示。由仿真实验可知，改进后的控制器不仅能够将系统控制在预设的稳定点，同时又消除了控制抖振现象，达到理想的控制预期。

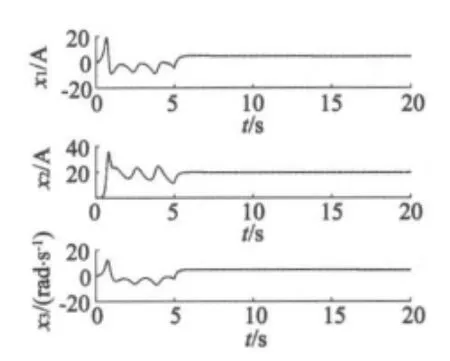
图8 状态变量时序图

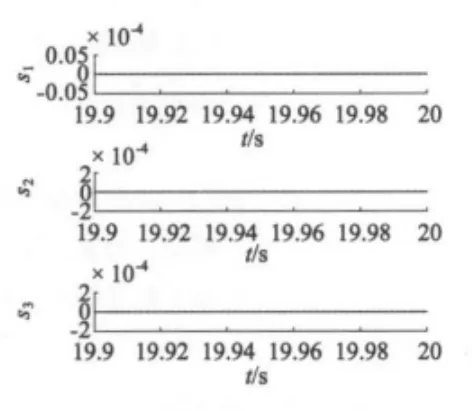
图9 改进型滑模面局部放大

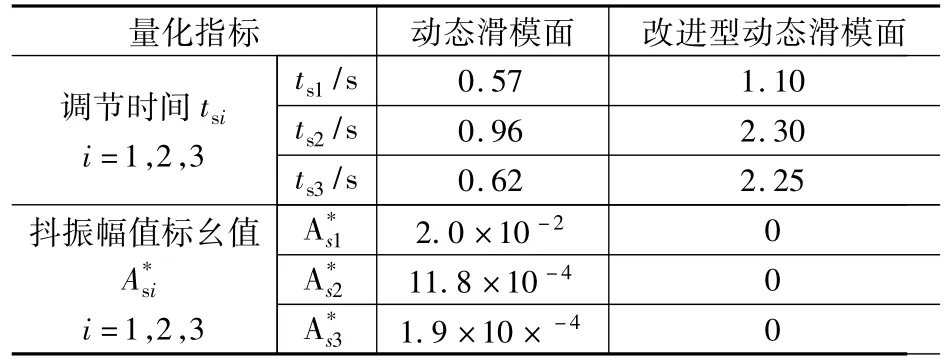
表1 两种滑模面对比

4 结 语

本文研究了无刷直流电动机系统混沌态的滑模控制，并得到了以下结论:

(1)提出一种基于三个控制器的动态滑模变结构控制策略，采用一种动态非线性滑模面和基于符号函数的等速趋近律，推导出相应的控制策略使无刷直流电动机混沌系统到达滑模面，并通过Lyapunov稳定性分析验证了控制策略的稳定性。

(2)针对滑模控制存在的高频抖振，设计一个改进型比例积分型滑模面，采用改进的趋近律并用饱和函数代替符号函数，推导出一种自适应无抖振滑模控制策略，消除了无刷直流电动机混沌系统的滑模控制抖振现象。

目前，滑模变结构控制在无刷直流电动机的混沌控制中的研究还有待深入研究，尤其是在实际应用场合，无刷直流电动机的运行状态受外界影响较大，如电源的电压电流变化、功率开关器件的谐波污染以及其它机电故障等，所以将自适应控制、模糊控制、神经网络控制等先进控制思想和粒子群算法、蚁群算法、模糊免疫算法等智能优化算法结合应用到滑模变结构控制中，实现混沌态的高性能控制，达到无刷直流电动机的高性能调速目标是今后的热点研究方向。

［1］袁晓明.煤矿蓄电池无轨运输车辆电控系统的关键技术研究［J］.电气开关，2011(1):18 －19.

［2］史文宏，宋长有.露天煤矿特种车辆转向系统EPS的设计［J］.露天采矿技术，2010:61－66.

［3］张昌凡，王耀南.滑模变结构的智能控制及其应用［J］.中国电机工程学报，2001(03):27－44.

［4］Feng Y，Yu X H，Man Z H.Nonsingular terminal sliding mode control of rigid manipulators［J］.Automatica，2002，38(12):2159 －2167.

［5］晁红敏，胡跃明.动态滑模控制及其在移动机器人输出跟踪中的应用［J］.控制与决策，2001(05):565－568.

［6］Yang J M，Kim J K.Sliding mode control for trajectory tracking of nonholonomic wheeled mobile robots［J］.IEEE Trans.on Rob.and Autom.，1999，15(3):578 －587 .

［7］唐超颖，沈春林.滑模变结构控制在航天器姿态控制系统中的应用［J］.兵工自动化，2004(1):4－6.

［8］邹德虎.电力系统自适应Terminal滑模控制研究［D］.南京理工大学，2010.

［9］王勉华，侯媛彬，刘存利.直流调速系统的滑模变结构控制［J］.电气传动，1992(5):4－6.

［10］Dadras S.Control of chaotic uncertain brushless DC motors［J］.IEEE International Conference on Control and Automation，2009:2143－2148.

［11］李秀春，徐伟，肖玉柱.一类受扰混沌系统的自适应滑模控制［J］.物理学报，2008(8):86 －93.

［12］王校锋，司守奎，史国荣.基于Terminal滑模的有限时间混沌同步实现［J］.物理学报，2006(11):125－130.

［13］杨国良，李惠光.直驱式永磁同步风力发电机中混沌运动的滑模变结构控制［J］.物理学报，2009，11(55):7552 －7557.

［14］邹伟全，姚锡凡.滑模变结构控制的抖振问题研究［J］.组合机床与自动化加工技术，2006(1):53－55.