基于细观理论的粗粒土剪胀性及本构模型

孙海忠

（1.同济大学 土木工程学院，上海 200092；2.上海岩土工程勘察设计研究院有限公司，上海 200032）

剪胀性是颗粒材料不同于一般连续体材料的重要标志.剪胀性是指土体在剪应力作用下体积发生膨胀的现象，无粘性粒状土在密实状态下易表现出剪胀性.粗粒土为单粒结构，颗粒之间存在咬合作用，在密度较大的条件下受剪切时，位于剪切面附近的颗粒必须以某种方式滑动、转动或折断以克服颗粒之间的咬合，寻求剪应变空间，致使体积发生变化.

土的剪胀性很早被发现并有了大量的研究工作，不少土的本构模型能够较好地模拟土的剪胀性，但未考虑实际的土体变形（如颗粒破碎等）是如何发生的，只是一种宏观的唯像论方法.一些学者对粗粒土的剪胀性进行了探索，Rowe［1］系统地研究了颗粒材料的变形机理，提出了最小能比原理，推导出了著名的Rowe剪胀模型.Ueng等［2］基于能量守恒原理和Rowe提出的最小能比原理从细观角度建立了考虑颗粒破碎的剪胀方程，在Rowe剪胀方程的基础上增加了1项颗粒破碎耗能因子，并通过试验对耗能因子进行了探讨，认为破碎耗能因子与破碎颗粒的表面积成正比.值得一提的是，以目前的试验条件很难对粗粒土的颗粒破碎表面积进行准确度量，因此，将该剪胀方程应用于实际模型中非常复杂，也不太现实；文献［3］也在Rowe剪胀方程的基础上增加了1项颗粒破碎耗能因子，通过粗粒土的大三轴试验研究提出了试样破坏时破碎耗能因子与围压成线性关系.然而在试验过程中不同围压下的颗粒破碎耗能因子会随着轴向应变的增加而不断增大，因此很难对围压进行归一化.如何准确地描述不同围压下颗粒破碎耗能因子在试验过程中的变化趋势，并将该考虑颗粒破碎的剪胀方程能够得以合理应用是本文探讨的关键.本文对Ueng等［2］建立的基于细观理论的粗粒土剪胀方程进行了改进，对不同围压下颗粒破碎耗能因子在试验过程中的变化趋势进行了归一化，并建立了相应的弹塑性本构模型.

1 基于细观理论的剪胀方程

Rowe［1］根据紧密粒状土体的受力平衡条件和变形相容条件考虑变形总是沿着能量耗散最小的路径进行推导得出著名的Rowe剪胀方程［4］，即

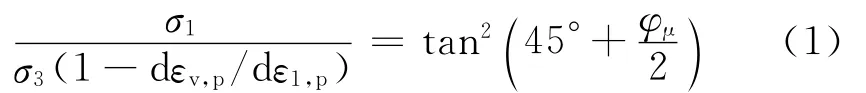
式中：σ1和σ3分别为最大和最小主应力；εv，p和ε1，p分别为塑性体积应变和轴向应变；φμ为颗粒之间的摩擦角.Rowe剪胀方程考虑了土体变形过程中的摩擦和颗粒滑移造成的剪胀耗能.紧密粗粒土在受力变形过程中除了摩擦与颗粒滑移造成的剪胀耗能外，颗粒的破碎造成的耗能也不可避免，特别是在高围压作用下，土体所受的约束作用增强，颗粒滑移的剪胀效应削弱，而颗粒破碎量变大，若不考虑颗粒破碎耗能效应显然是不合理的［4］.

在大三轴应力条件下紧密粒状土体受力及变形如图1所示，图中，βi为颗粒之间的接触面与铅垂方向的夹角；F1i，F3i分别为颗粒之间接触力在铅垂方向和水平方向的分量；Si，Ni分别为颗粒之间接触力沿颗粒作用面切向和法向分量；ui为颗粒之间的相对位移，yi，xi分别为颗粒之间相对位移在铅垂方向和水平方向的分量.文献［2-3］在Rowe剪胀方程的基础上从细观角度考虑破碎能耗的修正，得到了以下修正的剪胀方程：

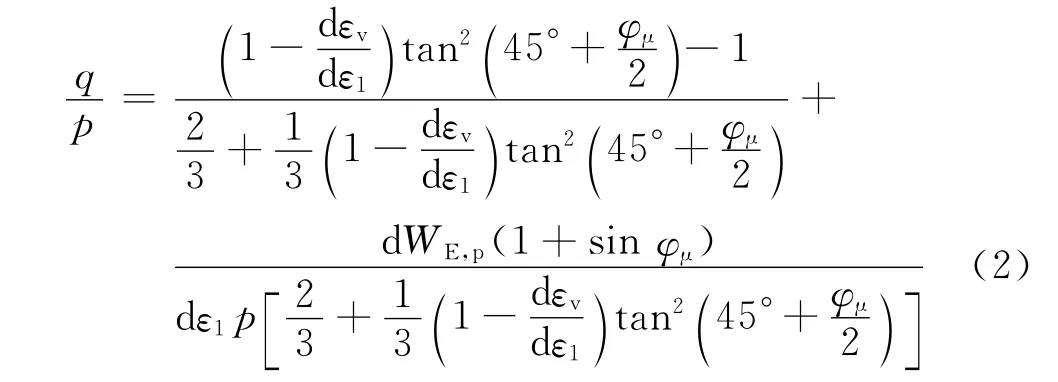
式中：q＝σ1-σ3；p＝（σ1＋2σ3）／3；dεv＝dε1＋2dε3，ε3为围压作用产生的应变；WE，p为单位体积粒状土体的颗粒破碎耗能（有效塑性功）.

在大三轴试验中由塑性轴向应变、塑性体应变、广义塑性剪应变三者之间的相互关系得到

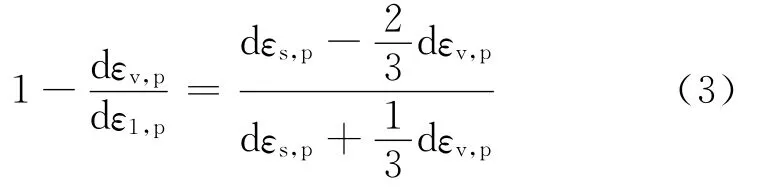
式中，εs，p为广义塑性剪应变.由硬化内变量 M＝得到

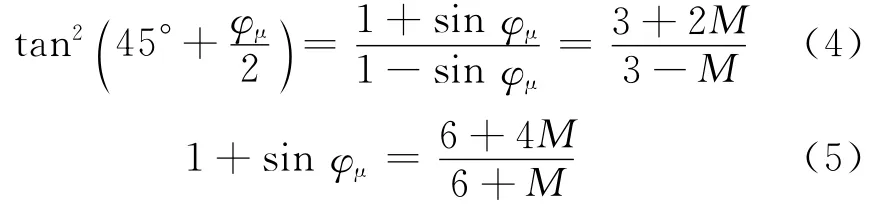
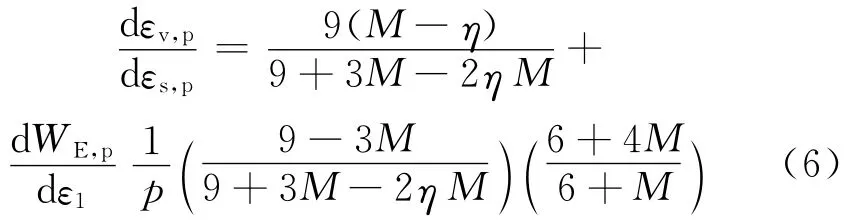
图1 紧密粒状土体的受力和变形［1］Fig.1 Loading and deformation of dense granular aggregates［1］

为了使上述剪胀性方程能够得到应用，这里关键在于dWE，p／dε1的处理.文献［2］认为 WE，p与破碎颗粒的表面积成正比，但实际上颗粒破碎表面积很难量测.文献［3］则认为WE，p与围压σ3成正比，但WE，p随轴向应变ε1的增加不断增大，因此很难直接对围压进行归一化.

对于WE，p的计算采用 Chavez等［5］提出的方法

式中：WR，p为颗粒重新排列所消耗的塑性功，一般假设为某一常数，该值较小，可以近似为零；WT，p为粗粒土在加载过程中所消耗的总功，即WT，p＝∫dWT，p，因此，dWE，p表示为

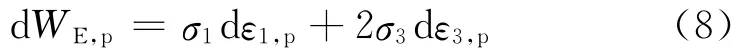
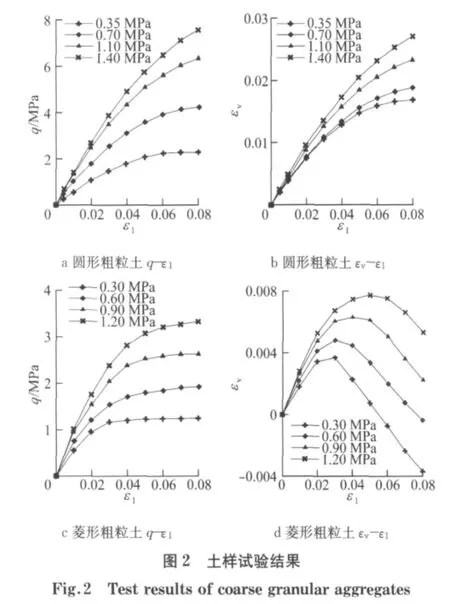
文献［6］开展了圆形、菱形颗粒形状的粗粒土大三轴排水应力-应变试验，如图2所示.

按照式（8）将颗粒破碎所消耗的有效塑性功WE，p分为2个部分进行计算，即轴向应力做功∫σ1dε1，p和围压做功∫2σ3dε3，p，相应计算结果如图3和4，将2个部分塑性功叠加得出WE，p随轴向应变ε1的变化趋势，如图5a和5c所示.经过数值分析，可以得到dWE，p／dε1随轴向应变ε1的变化关系，如图5b和5d所示，而ε1与WE，p存在着一一对应关系，因此，dWE，p／dε1可以表示为关 于 有效塑性功WE，p的函数，即dWE，p／dε1＝f（WE，p）.

通过相关计算，得到了2组土样剪切时dWE，p／dε1与有效塑性功WE，p的变化关系，如图6a和6c所示.可以发现，两者几乎呈双曲线关系，这里建议采用如下关系式进行表述：

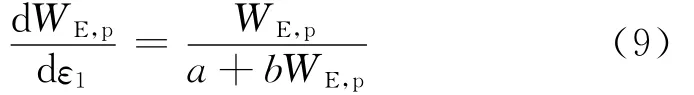
式中：a为dWE，p／dε1与WE，p关系曲线初始切线模量的倒数；b为其关系曲线强度极限值的倒数.用式（9）对2组结果进行最小二乘法非线性拟合，得到如图6a和6c中虚线所示.相对应的拟合参数a，b见表1.

图4 菱形粗粒土塑性功Fig.4 Plastic work associated with angular coarse granular aggregates sample

从表1可见，离差系数均小于0.05，符合拟合精度要求.参数a几乎没有变化，可以取4种围压下的平均值作为模型参数，圆形和菱形粗粒土的土样参数a分别为0.0099和0.0072.而参数b则随围压的增加而减小，如图6b和6d所示，两者几乎成线性关系，可以表示为

式中：k为比例参数；c为拟合直线截距.由图6b和6d的拟合结果得出圆形和菱形粗粒土土样的k值和c值分别为-0.29，0.46和-0.61，0.92.

将式（9）和式（10）代入式（6），得到最终的剪胀方程

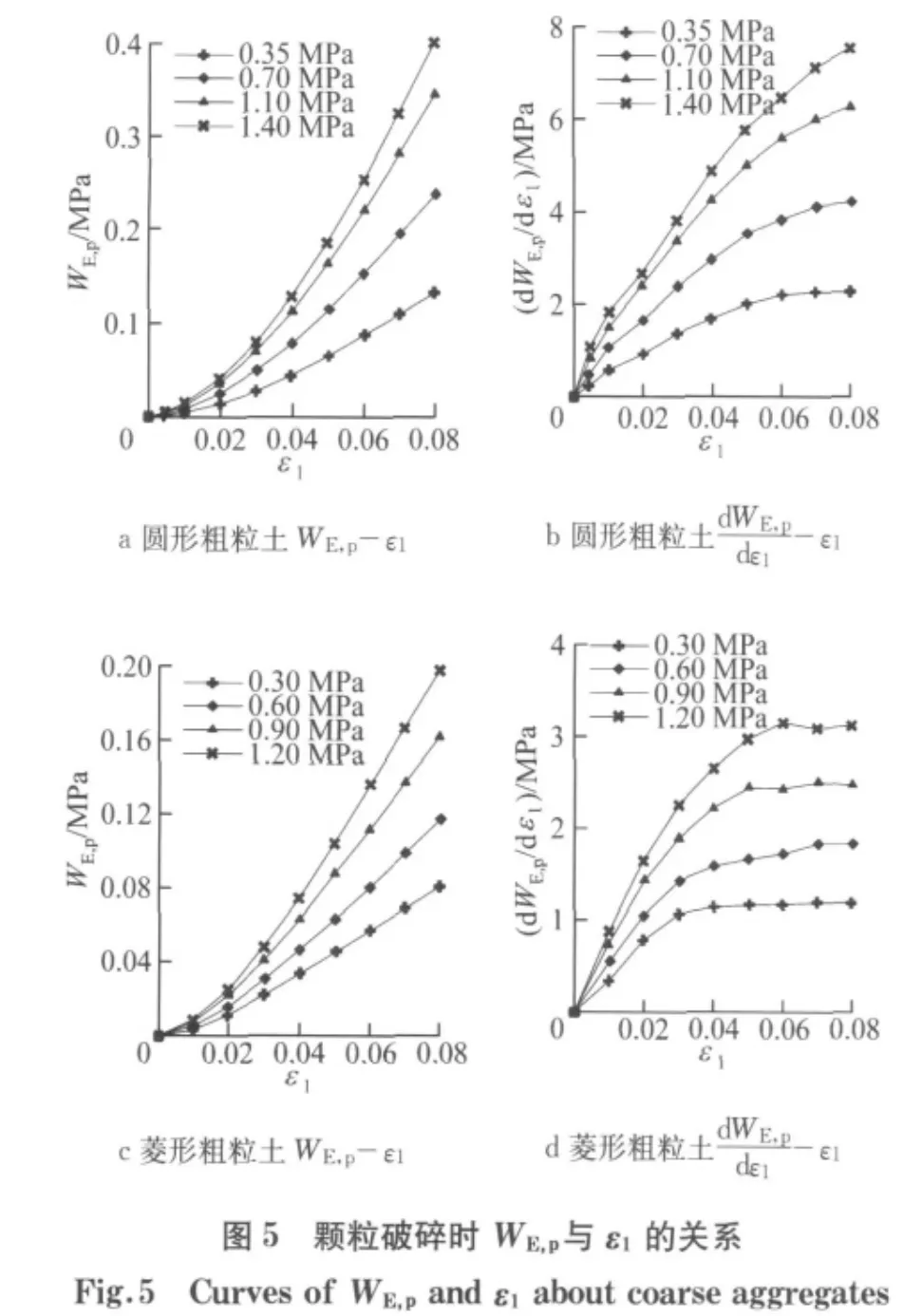
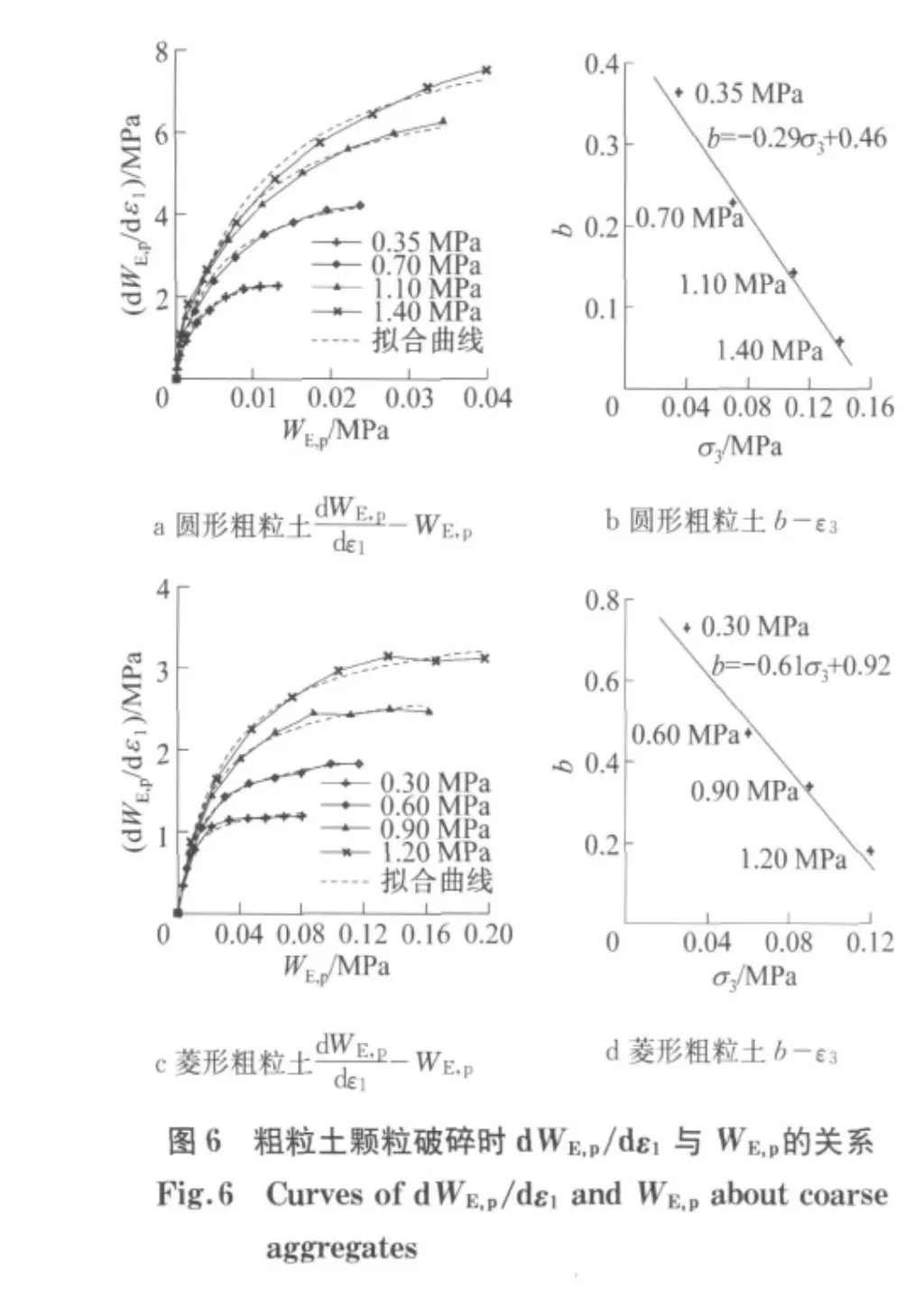
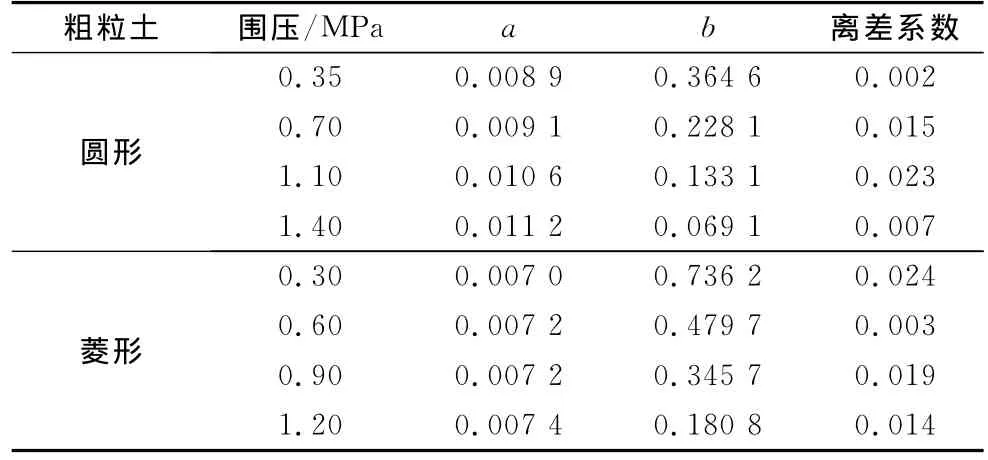
表1 粗粒土回归系数Tab.1 Regression coefficient of rounded coarse aggregates

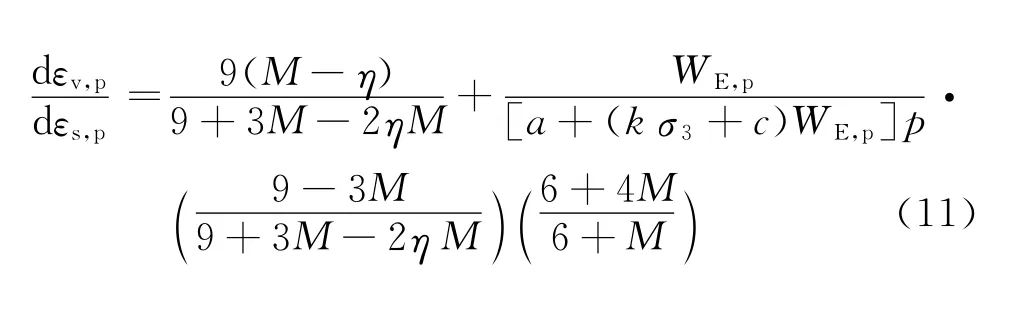
2 本构模型的建立与验证

2.1 模型的建立

这里通过将前面推导出的剪胀方程代入到相关本构模型来对室内颗粒破碎试验进行数值分析，从而间接地验证该剪胀方程正确与否.

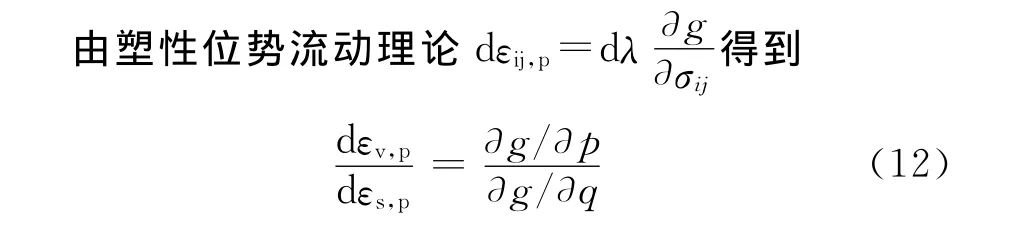
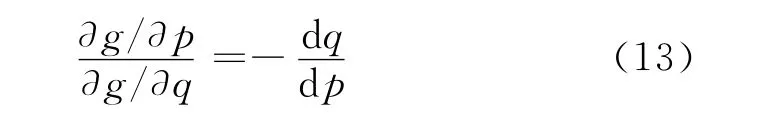
联立式（12）和式（13）得到

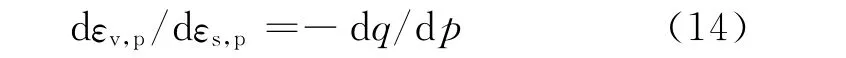
将式（14）代入式（6）得到塑性势方程

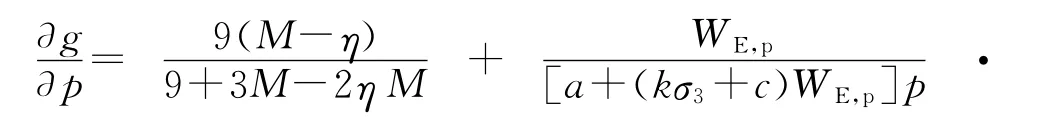
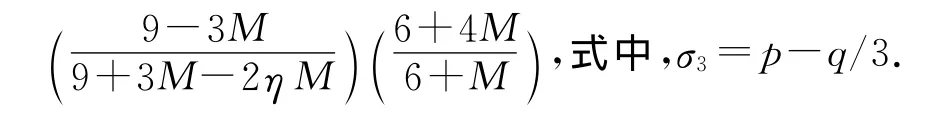
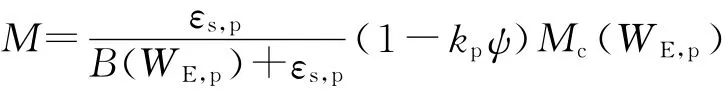
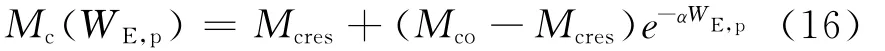
式中：Mco和Mcres分别为试样在剪切过程中随着有效塑性功WE，p的增加而表现出的初始状态应力比和残余状态应力比；e为孔隙比；α为有效塑性功参数.

为了应用该本构模型模拟粗粒土在不同加载水平下的应力应变关系和颗粒破碎程度，用FORTRAN语言编制相应的点积分程序并通过显式积分格式求得各计算步应力增量、塑性剪应变增量、塑性体应变增量，同时进行逐步累加得到应力和应变全量.在对 WE，p、临界状态应力比 Mc（WE，p）数值计算时其迭代过程为（WE，p）n＋1＝（WE，p）n＋dWE，P，dWE，p＝ qdεs，p＋ pdεv，p， ［Mc（WE，p）］n＋1＝［Mc（WE，p）］n＋d Mc（WE，p），d Mc（WE，p）可通过 对式（16）微分得到

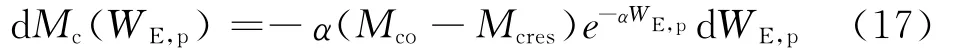
2.2 模型验证

为了验证模型的适用性，拟针对文献［6］开展的圆形（包括亚圆形）和菱形（包括亚菱形）2种颗粒形状的粗粒土大三轴颗粒破碎试验结果（2种粗粒土的临界状态线在e-ln p平面中均为直线型），用该模型对粗粒土在不同围压下的强度和变形特性进行数值模拟.首先分别将这2种粗粒土的试验结果绘制在e-ln p平面中，得出它们的临界状态线，如图7所示，图中ec为临界状态孔隙比.

图7 粗粒土的临界状态线Fig.7 Critical state line of coarse aggregates

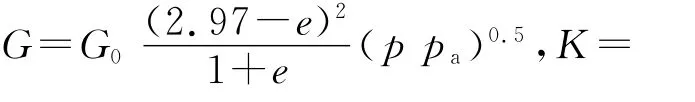
根据文献［8］提出的参数确定方法得出其他模型参数，模型参数如表2所示，表中，Γ，λ为临界状态线ec＝Γ-λln p中拟合参数.模拟结果与试验结果的对比如图8所示.

表2 模型参数Tab.2 Model parameters

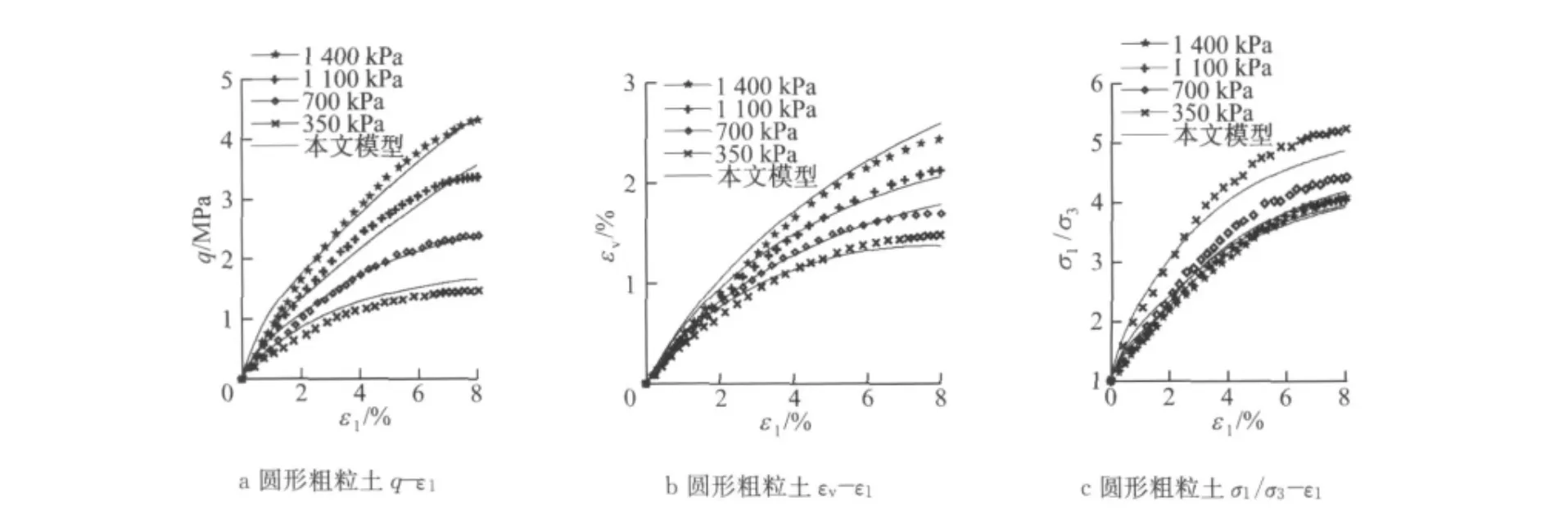
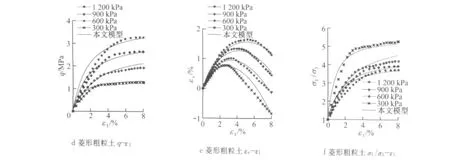
图8 粗粒土试验数据与模拟结果Fig.8 Comparison between data and simulation for coarse granular aggregates sample

由图8可知，本文模型不仅可以比较准确地预测剪应力q和轴向应变ε1的关系，还可以反映剪缩和剪胀特性对平均应力的依存性，即随着围压σ3的增大，剪胀性减小，剪缩性变大.

另外可以发现，圆形粗粒土的剪胀性较小，而菱形粗粒土的剪胀性较为明显，表明颗粒形状对于粗粒土的剪胀性具有一定的影响.值得一提的是，本文模型能够在较大应变范围内较好地描述粗粒土随着应力水平的增长由体缩向体胀发展的体变特性，证明了本文所推导出的考虑颗粒破碎的剪胀方程能够较好地描述粗粒土的剪胀特性.

3 结语

基于细观理论本文在Ueng和Chen提出的考虑颗粒破碎粗粒土剪胀方程的基础上对不同围压下颗粒破碎耗能因子在试验过程中的变化趋势进行了归一化，建立了仅与颗粒破碎所消耗的有效塑性功直接相关的剪胀方程.为了验证该剪胀方程的正确性，引用笔者曾提出的修正硬化准则，建立了考虑颗粒破碎的粗粒土弹塑性本构模型，对2种不同颗粒形状粗粒土室内大三轴试验的数值模拟表明，该模型能够在较大的应变范围内很好地描述粗粒土的应力-应变及体变特性，从而间接地证明了本文所推导出的考虑颗粒破碎剪胀方程的正确性.

［1］Rowe P W. The stress-dilatancy relation for the static equilibrium of an assembly of particles in contact ［J］／／Proceeding Royal Society，1962，269（1339）：500.

［2］Ueng T S，Chen T J.Energy aspects of particle breakage in drained shear of sands［J］.Geotechnique，2000，50（1）：65.

［3］Indrartna B，Salim W.Modeling of particle breakage of coarse aggregates incorporating strength and dilatancy ［J］.Geotechnical Engineering，2002，4：243.

［4］迟世春，贾宇峰.土颗粒破损耗能对罗维剪胀模型的修正［J］.岩土工程学报，2005，27（11）：1266.CHI Shichun，JIA Yufeng.Rowe’s stress-dilatancy model modified for energy dissipation of particle breakage［J］.Chinese Journal of Geotechnical Engineering，2005，27（11）：1266.

［5］Chavez C，Alonso E E.A constitutive model for crushed granular aggregates which includes suction effects［J］.Soils and Foundations，2003，43（4）：215.

［6］Varadarajan A，Sharma K G，Venkatachalam K.Testing and modeling two rockfill materials［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，2003，129（3）：206.

［7］Pietruszczak S，Stolle D.Modeling of sand behavior under earthquake excitation［J］.International Journal for Numerical and Analytical Method in geomechanics，1987，11：221.

［8］孙海忠，黄茂松.考虑颗粒破碎的粗粒土临界状态弹塑性本构模型［J］.岩土工程学报，2010，32（8）：1284.SUN Haizhong，HUANG Maosong.A critical state elastoplastic model for coarse granular material incorporating particle crushing［J］.Chinese Journal of Geotechnical Engineering，2010，32（8）：1284.

［9］Li X S，Dafalias Y F.Dilatancy for cohesionless soils［J］.Geotechnique，2000，50（4）：449.