利用椭圆烈度衰减关系确定历史地震震级与震中

吴 清 高孟潭

(中国地震局地球物理研究所，北京 100081)

1 方法

利用地震烈度宏观考察资料即烈度信息点(x,y,I)，联立烈度椭圆衰减关系及考虑中心点和方向性的椭圆数学方程，计算地震震中平面坐标(x0，y0)和震级M，以及椭圆长轴与x轴夹角θ，见方程(1)：

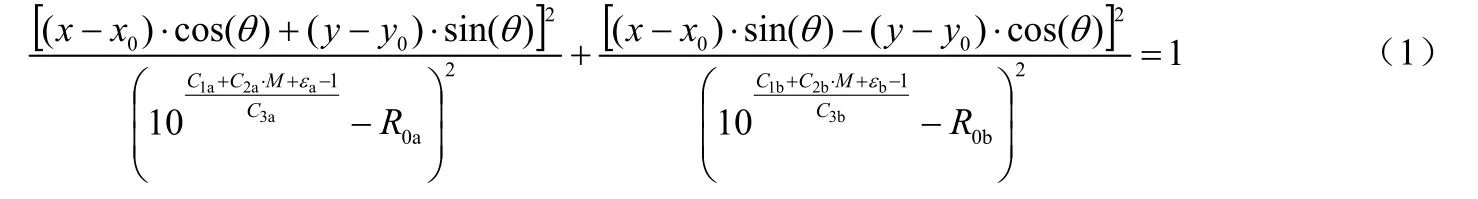
式中(x,y)是烈度信息点平面坐标；(x0，y0)为椭圆中心坐标，即地震震中平面坐标；θ(0°≤θ≤180°)是椭圆长轴逆时针与x轴正方向的夹角；系数C1a，C2a，C3a，及C1b，C2b，C3b分别为椭圆烈度衰减关系长短轴回归系数；I为烈度，M为震级；R0a，R0b。分别为长短轴两方向烈度衰减的近场饱和因子；εa、εb为椭圆烈度衰减回归分析中表示不确定性的随机变量，通常假定为对数正态分布，其均值为零，标准差为σa和σb。

已知一个地震的多个烈度信息点(xi,yi,Ii)，求震中(x0，y0)、震级M和方向，转化为求取方程(1)的最优解。有4个未知数，则至少需要4个方程确定一组解，但x0与y0不是相互独立的，因此在椭圆衰减模型下，3个烈度信息点就能确定一组解。烈度信息点增多，变成解超定非线性方程组，采用麦夸特法（Levenberg-Marquardt）＋通用全局优化法的数值计算方法寻求最优解。

理论上，烈度信息越多对恢复历史地震参数越有利，但实际历史地震史料稀缺，希望尽可能的利用较少的烈度信息点得到较可靠的地震参数。历史地震资料有限，运用蒙特卡洛方法，对信息丰富的现代地震烈度点抽样，模拟历史地震烈度点分布情况。先从烈度信息点中随机抽取3个点，并且有放回的重复抽样100次。增加控制信息，添加烈度点数，随机重复抽取8点、15点、20点各100次，带入方程(1)计算。每次抽样代表不同的烈度点空间分布，而不同的烈度点数代表了烈度信息的多寡，真实历史地震资料记载只相当于随机抽样中的一种情况，通过蒙特卡洛模拟来分析此方法计算历史地震震级与震中的不确定性。

2 结果

选取最新近出版的4册《中国震例（1992—2002）》，提取其中既有仪器记录数据又有烈度数据的现代地震进行大量验算。以2000年1月15日云南姚安宏观震中为（101.177°E，25.640°N）的MS6.5地震为例，取五代区划图中川藏地区椭圆烈度衰减关系式，可以看到3个烈度点是基本要求，没有限制信息，定出来的震中很发散，具有很大的不确定性。其抽样震中与真实震中之间最大差距达165 km，平均值为21.46 km，仅35%的差距在10 km以内（历史地震1类精度）。随着抽样烈度点的增加，抽样震中逐渐朝真实震中收敛，15个烈度点时已基本趋于稳定，其抽样震中与真实震中的最大差距为16 km，平均值为6.8154 km，80%的差距都在10 km以内（历史地震1类精度）。

对震级结果进行统计分析，发现随着烈度点的增多，抽样计算所得震级值也逐渐朝仪器参数靠拢，标准差也越来越小。3个烈度点时，抽样震级值与真实震级的差值在[－1，1]区间内，差值均值为－0.1185，标准差为0.378；15个烈度点的抽样震级值与真实震级的差值在[－0.2，0.4]区间内，差值均值为0.0462，标准差为0.15。虽然计算结果与真实地震参数之间存在差异，但随着烈度点数的增大，差异逐渐缩小到可控范围之内。可用大量现代地震统计在不同地区不同大小地震的不同烈度点数和烈度点分布情况下的不确定性范围，经假设检验后给出置信区间对计算结果加以约束。

3 结论

大量现代震例充分证明，可直接将烈度信息点带入到椭圆烈度衰减关系与椭圆数学方程联立的方程组，计算地震震级和震中。此方法尽可能多的利用了原始烈度资料里的信息，减少人为主观判断带来的偏差，对于仅有烈度资料的历史地震，尤为适用。