运用“三讲”模型来讲题

孙瑛

摘 要：湖南省长沙市雨花区砂子塘小学四年级数学组在进行“小老师话语系统”在四年级习题教学中的实践研究时，运用“三讲”模型训练学生讲解习题：讲清信息点、讲全解题点、讲好拓展点，不仅能提升学生的数学语言能力水平，同时也能够促进学生思维水平与数学语言表达情感的发展。

关键词：“三讲”模型;信息点;解题点;拓展点

中图分类号：G623.5 文献标识码：A 收稿日期：2019-07-12 文章编号：1674-120X（2019）31-0068-02

一、讲清信息点

讲题从读题开始。这要求讲题者首先要准确、流利、大声地通读题目，不加字、不减字;注意读题的轻重缓急，注意读题的快慢节奏，认为关键的字、关键的词可以重读。接着，讲题者要很从容地在题目中标出关键句，圈出关键字、关键词，正确领会题目意思，进行自我理解上的分析，讲清所有信息点，讲清哪些信息是有用的，让听题者能清楚地听出题目的情节内容、知晓题目的条件与问题、明白期间的数量关系，能将所有有价值的信息进行整合，从而建立起完整的表象。

学生讲清信息点例1：

同学们好，今天我讲的是数学书第54页的第2题，我们先来读题。

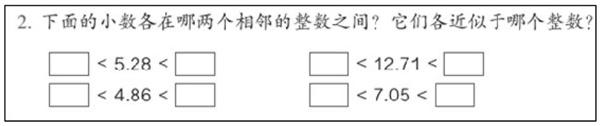
“下面的小数各在哪两个相邻的整数之间？它们各近似于哪个整数？”（黑体字一般会重读）

通过读题，我们知道了这个题目是有两问的。我们先看第一问，关键词、关键句有：小数、两个相邻的整数。这是要我们判断题中的各个小数分别在哪两个相邻的整数之间。再看第二问，关键词是近似于、整数，实际上是要我们根据四舍五入法将这些小数保留整数。同学们，请注意了，第一问是直接填空，一般是不会漏填的，但是第二问就容易忽视了，千万要注意审题，有几问就一定要答几问。

学生讲清信息点例2：

同学们好，今天我讲的是数学书第89页的第6题，我们先来读题。

“先根据对称轴补全下面这个轴对称图形，再画出这个轴对称图形向右平移10格后的图形。”（黑体字一般会重读）

通过读题，我们知道了这个题目是操作题，并且有两个操作要求。第一个要求是补全这个轴对称图形，第二个要求是将这个轴对称图形向右平移10格。同学们，一定要细心，题目有几个要求，我们就一定要完成好几个要求。特别注意平移时的方向和格数。

坚持这样的读题模式，不仅能使讲题者的审题意识增强，所有的听题者也会在倾听中跟着形成对信息的输入、处理、输出的良好审题习惯。

二、讲全解题点

会解题≠会讲题，四年级学生的数学语言表现出“抽象与直观并存，直观多于抽象”的特性，教师要求学生在讲清了题意的基础上，鼓励他们借助文字、图形、表情和动作等，用准确、流畅、完整、有条理、比较精准的数学语言讲全解题点，包括解题思路、解题方法，突出重点、难点，提醒易错点、抓住关键点。

学生讲全解题点举例：

同学们，刚才我们通过读题，已经截取了有用的信息：

总人数：32人;大船30元载6人;小船24元载4人

这样理清信息，是接下来解题的关键。要想解决怎样租船最省钱的问题，我们先得知道大船每个座位是多少钱，小船每个座位是多少钱。我们可用总价除以数量求得单价。

大船每个座位的价钱：30÷6=5（元）

小船每個座位的价钱：24÷4=6（元）

5元<6元，说明租大船便宜些，尽量要租大船。

接着，我们要算出32人如何租船，并算出租船的价格是多少：32÷6=5（条）……2（人）

从这个算式的结果可以看出，要租5条大船，1条小船，可是小船会空出2个座位。总价为：5×30+24=174（元）

现在，我们应重点思考，如果不空座位，会不会更省钱？

调成4条大船和2条小船，这是这类题目的难点，并不是大船少一条，就对应着小船多一条，一定要计算所坐的总人数。我们来看，4×6+2×4=32（人），正好可以坐下，再算租船的总价只有：4×30+2×24=168（元）

168元<174元，显然租4条大船和2条小船是最省钱的。

学生讲全解题点并不是件容易的事情，从“会做”到“会讲”，再到“讲会”，是需要过程的，教师在倾听的过程中，可以肯定学生思考的合理部分，听出学生的思考漏洞，纠正其解题时的误区，同时也可以协调师生思维之间的差异，架起师生之间的解题桥梁。

三、讲好拓展点

教师可以鼓励学生拓展讲题，不要拘泥于就题讲题，以原题为基点，争取一题多变，灵活地处理题目，或在已知与未知之间转换，或增加、减少、改变条件，或改变问题，在改变中提升学生对题目的深入思考，让其讲出对题目的独特见解。另外，四年级的习题，有许多题目可以一题多解，教师应抓住习题特点，鼓励学生从具体题目出发，确定思维起点，沿着不同的思考方向，从不同的角度，运用不同的思维方式，讲出不同的解答方法。

学生讲全好拓展点举例：

同学们，我们可以看到，这块菜地的形状是不规则的，要求它的面积，我们应该变不规则为规则。方法有很多，我先来讲第一种：

方法1：可如右图将这块菜地补全成一个完整的长方形。

大长方形的面积-空白长方形的面积 = 菜地面积

大长方形的长是9米加19米的和，宽是21米，面积是（9+19）×21=588（平方米）

空白长方形的长是19米，宽是21米减去9米的差，面积是19 ×（21-9）=228（平方米）

菜地面积是588-228=360 （平方米）

方法2： 我们也可以如右图这样将菜地进行分割。

上面长方形面积 + 下面长方形面积 = 菜地面积

上面长方形的长是21米减去9米的差，宽是9米，面积是（21-9）×9=108（平方米）

下面长方形的长是9米加19米的和，宽是9米，面积是（9+19）×9=252（平方米）

菜地面积是252+108=360（平方米）

方法3：我们还可以如右图这样将菜地进行分割。

左面长方形面积 + 右面长方形面积 = 菜地面积

左面长方形的长是21米，宽是9米，右面长方形的长是19米，宽是9米，菜地面积是  21×9+19×9=（21+19）×9=360（平方米）

同学们，我们来比较这三种方法，都可以顺利求出菜地的面积，但是只有第三种分割的方法，可以得到最直接的数据，再加上乘法分配律的的运用，可以快速而正确地求得答案，这也是为什么要把这个习题安排在“运算定律”这个单元的原因吧。

当然，方法2和方法3 ，也可以带给我们不一样的思考，分割的两个长方形的宽都是9米，那么我们可将其中一个长方形旋转，将两个长方形拼接成一个大的长方形。而方法3的拼接，可以一目了然地看到大的长方形的长与宽的数据。

就这样，一批学生慢慢地成长起来，为了更好地讲好一个题目，讲出新意，讲出不一样，学生会深入思考，会从不同的角度去思考题目的外延，不断挖掘题目的内涵，在无形中探究精神得到熏陶和培养。

在“小老师话语系统”训练下，以数学语言为切入口，通过“讲”来促进思维发展的“三讲”模型对四年级学生是有效适度的，不仅能提升小学生的数学语言能力水平，同时，也能够促进学生思维水平与数学语言表达情感的发展。在讲题实践中，展现其强大的优势与生命力，实现了教育的高效与持续性，值得教师们进一步探索、实践与研究。

参考文献：

[1]张文超.小学生数学语言能力发展的教学模型研究[D].重庆：西南大学，2017.

[2]刘 能，王正燕.论小学生数学语言表达能力培养的重要性[J].考试周刊，2011（13）：103-104.