偶完全数有无穷多

陈德建

（黎明职业大学，福建 泉州 362000）

偶完全数有无穷多

陈德建

（黎明职业大学，福建 泉州 362000）

本文从完全数的定义出发，运用已证得的定理，并利用梅森合数的性质，求出两梅森数下标素数的关系；用反证法，假设存在最大梅森素数，从而引出矛盾，证明命题。

完全数；偶完全数；梅森数；梅森合数；梅森素数；最大梅森素数；反证法

一、引论

定义1：设n是一个正整数，如果n的全部因数的和等于2n，n就叫做一个完全数（perfect number）。

例如，6的因数的和σ（6）=1+2+3+6=12，28的因数的和σ（28）=1+2+4+7+14+28=56，故6和28都是完全 数①。

定义2：形状是 Mn=2n-1的数叫梅森（M·Mersenn）数。

定理1：如果n＞1，且an-1是素数，那么a=2,且n是素数。

证：如果a＞2，又因n＞1，所以1＜a-1＜an-1，且an-1=(a-1)(an-1+an-2+…+a+1)，所以an-1有真因数（a—1），即它不是素数了，因此a=2。如果n是复合数，即n=kl，其中1＜k＜n，那么1＜2k-1＜2n-1，且（2k-1）丨（2n-1），从而2n-1也将不是素数了。所以如果an-1是素数，则必须a=2及n是素数。

定理证完。

定义3：如果p是素数，且 Mp=2p-1也是素数，则Mp称梅森素数。

例 如 22-1=3,23-1=7,25-1=31均 为 素 数 ， 故M2,M3,M5均为梅森素数。

但并不是所有Mp均为梅森素数，例如等等②。

显然，n是合数时，an-1是合数，而Mp中也有合数，本文所称梅森合数是指Mp中的合数。已知的前33个梅森素数依次是

这第33个梅森素数 2859433- 1有258716位。

Mersenne prime（梅森素数）的个数无疑是无限的，但其证明却毫无希望地超出了我们的能力。③

定理 2：如果Mp是素数，那么(2p- 1)是一个偶完全数，而且除了这些以外，在没有其他的偶完全数。

证：我们用σ(n)表示n的全部因素之和，如果Mp是素数，那么的因数显然为1，2，所以

现在假定a是一个偶完全数，假设a的标准分解式中含2的最高方幂的次数为n-1，因a是偶数，所以n-1≥1，又因 2n-1显然不是偶完全数，所以a= 2n-1u，u＞1，2u。

因此a的因数为所有形如2iv的数，其中0≤i≤n-1及vu。从而 2nu=2a=σ(a)= (1+2+…+2n-1)σ(u)=σ(u)(2n-1)，即得是整数。另一方面，由上面等式得到都是u的因数，而σ( u)又是u的所有因数的总和，所以u只有两个因数u和因u＞1及u至少有两个因数u和1，所以必须换句话说，u是一个素数，且u= 2n-1。由定理1，n必须是素数。

定理证完。

这个定理说明，是否有无穷多个偶完全数的问题，即归结为是否有无穷多个梅森素数的问题。④

是否有无穷多个p使Mp为素数，是数论中尚未解决的难题。

值得注意的是梅森素数在一些应用学科（如代数编码）中得到应用。⑤

定理 3（拉格朗日）：假定 p是素数，那么同余方程f(x)=anxn+an-1xn-1+…+a1x+a0≡0(Modp)，1≤x≤p……（1）的解数≤n，重解也计算在内。这里an,an-1,…，a1,a0都是整数，且pan。

证：如果（1）没有解，那么定理成立。如果x=α是（1）的一个解，那么（1）式可以写成 f(x)=(x -a)f1(x)+r1，以x=α代入得所以 f(x)≡(x - a)f1(x)(Modp)，如果x=α又是 f1(x)≡ 0( Modp)的解，那么同样可得f1(x)≡(x - a)f2(x)(Modp)。 这 时 我 们 称 α做f(x )≡ 0(Modp)的重 解 。 继续 下 去 ，如 果f(x)≡(x -a)kg1(x)(Modp)，其中g1(x)≡/ （0 Modp)，就称a是f(x)≡0(Modp)的h重解。

由证明可以看出 g1(x)的次数是 n－h。设（1）另有一解x=b，那么所以有 g1(b)≡（0 Modp)。如果x=b是 g1(x)≡（0 Modp)的K重解，那么同样有这样继续进行下去可得，其中g(x)的次数是n-h-k-…-l，且 g (x )≡（0 Modp)不再有解，所以f(x )≡（0 Modp)的解数是 h +k+…+l ≤n。定理证完⑥。

定义4：假定m是一个自然数，如果（ n ,m)=1，且同余式 x2≡ n(modm)有解，我们就称n做模m的二次剩余。如果上面的同余式没有解，n就叫做模m的二次非剩余。

例如1，2，4是模7的二次剩余，而3，5，6是模7的二次非剩余。

用p除所得的余数，就是模p的全体二次剩余。

证：用p除（1）中各数所得的余数，显然都是模p的二次剩余，现在要证明的是：1，2，…，p－1中，模p的二次剩余也就是这些。

假定1≤n p＜。如果同余式

有解，那么由拉格朗日定理可知它至多有二个解，由（p-x)2≡(-x)2≡x2≡n(modp)可知（2）还有一个解p- x。如果那么 1≤p－x≤因此如果（

2）有解，它总会有一个解适合于

换句话说，如果n是模p的二次剩余，那么n必定模p同余于（1）中的一个数。因此剩下来要证明的就是n中是模p的二次剩余恰有个，这只要证明（1）中的任何两个数模p都不同余。假定 a2,b2是（1）中的任何二数，且a＞b，如果 a2≡ b2(modp)，即得，由于p是素数，可知但1≤a+b＜p， 1≤a-b＜p，这是不可能的。因此（1）中任何二数都是模p互不同余。 定理证完⑦。

定理5（费马小定理）：如果p是素数，那么对于任何整数a都有 ap≡a(mod p)

中的一个，这是因为用p除n后的余数总是其中之一。假定在这p-1个数中任取两个不同的数k1与k2，现在来

模p分别同余于（1）中的一个数，而且（3）中的数又彼此对模 p互不同余。又因从c≡d (mod p)与c＇≡d＇(mod p)可 以 推 出cc＇≡ dd＇ (m od p)，所以（1）中各数相乘的积同余于（3）中各数相乘的积，因此

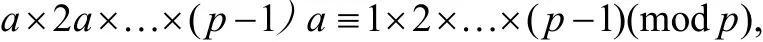
(p-1)！ap-1≡(p-1)！(modp),即因此p是素数，所以p（p-1)！，故有即得

定理6（欧拉）：当p为素数时，有关系式

证：假定n是模p的二次剩余，那么同余式x2≡ n(modp)有解x，即所以由

推论：当n＝2，p为奇素数时，由欧拉定理有

定理7：设p是一个奇素数，q是Mp的一个素因数，则q形如 q = 2 kp +1。

证明这个定理之前，先证一个简单的引理。

引理：设 a＞0,b ＞0 ,s ＞1，则

证：不妨设a＞b，由辗转相除法得

定理证完。⑩

二、证明

以下我们来证明梅森素数有无穷多。

设q、p均为奇素数，且p q＞ ，由欧拉定理的推论知存在正整数A、a,使得

令p- q =2t，显然t是正整数。若Mp不是素数，即Mp为梅森合数，由定理7知存在正数m、n，使得

由于2p-1不是一个完全平方数,所以m≠n，不失一般性，不妨设m＞n。由（1）有 m+n≡±2a(modp),设m+n=bp±2a，我们来证b＞0。

由（1）有 2mn= a2-b ，由（2）有b＞0。

由（1）式及a为奇数， a2p ± 2a为奇数，m+n必为奇数，所以 m与 n必一奇一偶，2mn是 4的倍数，a2≡1(mod4)，所以 b≡1(mod4)。

事实上 p=11时 ， a =3,m=4,n =1,b=1；

我们用反证法证明之。

设梅森素数为有限个。则存在奇素数q，使 Mq=2q-1为最大梅森素数，对任何 p= q +2t的奇素数p，Mp均为梅森合数。

由费马小定理 2q-1≡ 1(mod q ),知存在正整数S，使

令C=4tS -2 mnp -m-n ，则（6）式变为

由算数基本定理知C＞0，C为奇数。由（7）式有

若4t＜p,则22t＜q+2t,22t-2t＜q 。事实上，当t=1时， 4t= 4t；当t＞1时，4t＞4t，例如t=2时， 42=16＞8 = 4×2。

设4t＜p,则22t＜q+2t,22t-2t＜q 。

事实上，当 t =1时，4t=4t,当t＞1时，4t＞4t ，例如t=2时，42=16＞8=4×2。

由（8）式，当 4t＜ p时，有2St -1＞C，

由于C 为奇数，故有2 St＞ C ，即

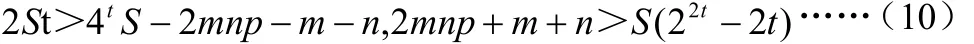
若n=1，有 2mp +m +1＞S(22t-2t)，

又有有2 mp+m ≤S (22t- 2t)，若n＞1，有 mn＞ m+n，

代入 (10) 2mnp +mn＞S(22t-2t)

由于 2mn= a2-b，由（11）式有

若a2-b＞ S ，必有a2＞S，即

由假设 4t＜p,又q＜p,∴ 4tq＜p2，得一矛盾。

故 a2-b＜S 。

若a2＜S ,必 有a2-b＜S。

若2St- 1＜p ， 当q=3时,A=1,S=1,

当q=5时, A=1,S=3,当 q=7时,A=1,S =9,

当q=11时 ,A = 3,S=81。

2St＜ p+1＝q+2t+1，2t (S -1)＜q+1,由于S≥1，恒有

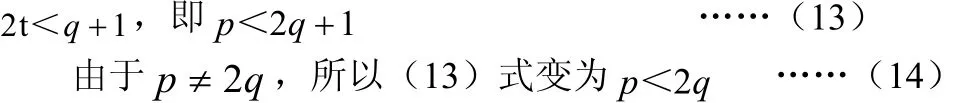
由 （8） 式 ， 当 2St-1＜p时 ，必有4t＞C， 即

当n=1时， 2mp +m ≥4t( S -1)

当n＞1时，m n＞m + n,代入（15），2 mnp +mn＞4t( S-1)

综之有 mn( 2p+1)≥4t(S-1)， 又有2 mn (p+1)＞4t(S-1)，(a2-b)(p +1)＞4t(S -1)， 必 有 a2(p +1)＞4t(S-1)，于是得一矛盾。即4t＜C。故第二种情形不存在。

综上所证，当Mp为梅森合数时，p＜2q。

由于素数有无穷多，因而大于q的素数也有无穷多，所以必有大于2q的素数p使Mp为素数，这与假设存在最大梅森素数相矛盾。所以，梅森素数有无穷多，因而偶完全数有无穷多。

证完。

[1] 王文才，施桂芬.数学小词典[Z].北京:科学技术文献出版社，1983.

[2][4][6][7][8][9] 王元.谈谈素数[M].上海：上海教育出版社，1983.

[3]［加］R.K.盖伊.数论中未解决的问题（第二版）[M].张明光，译.北京：科学出版社，2004.

[5][10] 柯召，孙琦.数论讲义（上）[M].北京:高等教育出版社，1990.

There are inexhaustible even perfect numbers

In this paper, beginning with the defination of perfect number, using some theorems, we applied the character of Mersenne composite number, found the relation of two primes subscripted to two Mersenne numbers, and assumpted existing the maximum Mersenne prime, derivated a paradox.Them, we proofed the proposition

perfect number; even perfect number; Mersenne composite number; the maxinum prime; derivate a paradox

CHEN De-jian

O1-0

A

1008-7427（2012）03-0156-03

2012-01-04

作者系黎明职业大学副教授，高级工程师。