函数连续的概念和极坐标下求面积时确定积分限教学浅见

李颖颖

（武汉职业技术学院 湖北 武汉 430074）

函数连续的概念和极坐标下求面积时确定积分限教学浅见

李颖颖

（武汉职业技术学院 湖北 武汉 430074）

介绍了关于函数连续的概念，并讲述了在授课中如何运用观察和分析图像的方法掌握函数在某点连续的条件以及在极坐标系下求面积时怎样确定积分限。

函数；连续概念；极坐标；积分限

在高等数学教学中，关于函数连续的概念和极坐标下求面积时如何确定积分限，常令学习者感到困惑。笔者根据多年的教学经验，总结出函数在某x0点处连续条件的图像解析方法，使学生能够直观地掌握函数连续的概念；又得出了极坐标中求面积时矢径r为正值的结论，使学生在极坐标系中求面积时能够简捷地确定出定积分的积分限。此教学经验使学习者在学习这两部分内容时不再感到困难。下面分别予以介绍。

关于函数在某x0点处连续条件的图像解析

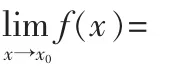
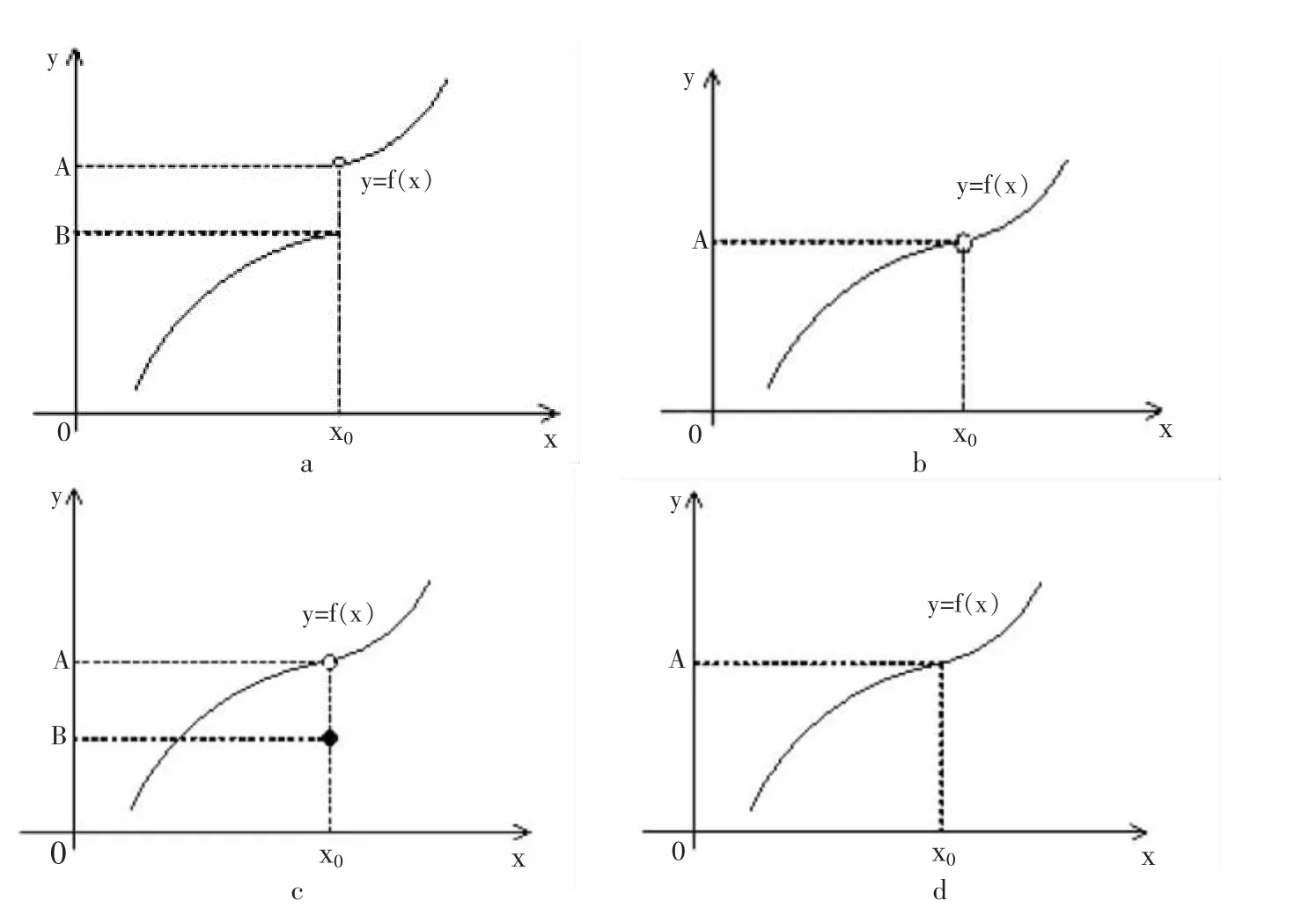
图1 函数连续的概念解析图

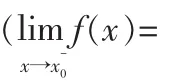
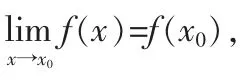
关于在极坐标系中求面积时积分限的确定问题

在极坐标下用定积分求曲线所围面积时，其难点在于如何准确确定出积分的上、下限。由于现行大学本科和专科的数学教材对此问题的阐述较少，学生（尤其是高职的专科生）在解题时普遍都感到困惑。笔者对此介绍些经验和体会。

在中学阶段学习极坐标方程时，矢径r的取值是可正可负的。但在求一个极坐标方程确定的曲线所围成的面积时，我们无需过多考虑这个面积的形状，只要始终将极坐标方程中矢径r的长度值，确定是不小于0的，然后就可直接利用极坐标方程定出积分的上、下限。

例如，在极坐标下用定积分求“心形线”所围成的面积时，首先要定出积分的上、下限，如果把矢径r看做是负值的，则由 “心形线”的极坐标方程r=a（1－cosθ）（a＞0）将得出1－cosθ＜0，即cosθ＞1，这结果显然是错误的，如此就无法得出θ的取值区间。但如果把矢径r看做是非负值的，则由方程得出 1－cosθ≥0，即cosθ≤1，于是可得0≤θ≤2π，这样就确定出了积分的上限为2π，下限为 0。上例中将矢径r视为非负值的做法是具有一般性的。该做法在极坐标系中求面积时能够帮助我们简捷地确定出定积分的上、下限。

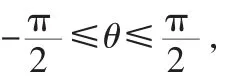
尽管现行的数学教材都没有明确指出矢径r的正、负，但在求一个极坐标方程确定的曲线所围成的面积时，我们可以把r当做非负值来看待。

对于求解由两曲线所围公共部分面积的问题时，我们首先需对包围着被求面积的两曲线的图像有一个大致的了解。这通常可用描点法将两曲线画出 ，然后联立两曲线的极坐标方程，求出两曲线的交点坐标，再结合两曲线的图像得出积分的上下限。

例1：求由圆r=a与“心脏线”r=a（1＋cosθ）所围重叠部分的面积（a＞0）。

解：列表（表略）作简图。取a=1画简图2。

图2

例2：求曲线r=acosθ与r=a（cosθ＋sinθ）所围重叠部分的面积（a＞0）。

解：列表（表略）作简图。取a=1画简图3。

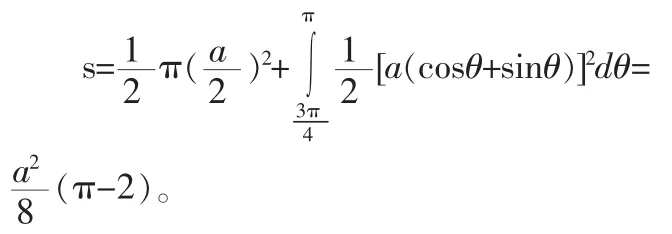
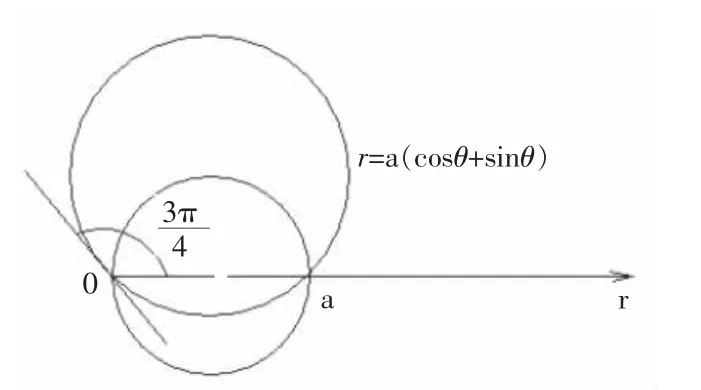
图3

结合曲线的图像可得两曲线所围公共部分面积s的积分为：

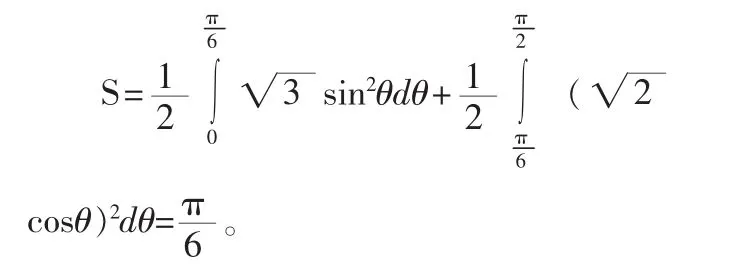
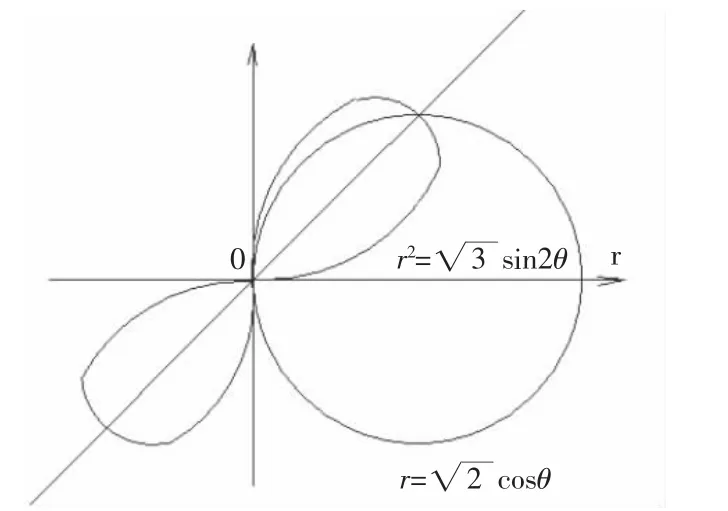
图4

[1]丁匡平.应用高等数学（第3版）上册[M].北京：国防工业出版社，2010：20.

[2]赵红革，颜勇.高等数学[M].北京：北京交通大学出版社，2008：137.

[3]俎冠兴.高等数学[M].北京：化学工业出版社，2007：18.

[4]曹瑞成，姜海勤.高等数学[M].北京：化学工业出版社，2008：131.

[5]郑桂梅.高等数学[M].北京：国防科技大学出版社，2008：44.

[6]朱永银，张敏.高等数学（上册）[M].武汉：武汉大学出版社，2004：175.

[7]方晓华.高等数学（第2版）[M].北京：机械工业出版社，2008：94.

[8]唐月红，刘萍，王东红.高等数学（上册）[M].北京：科学出版社，2008：202.

[9]张锦麟，时晓文.高等数学[M].北京：中国铁道出版社，2007：28.

G712

A

1672-5727（2012）05-0115-02

李颖颖（1955—）男，武汉职业技术学院副教授，研究方向为高等数学教学。