基于二维稀疏表示和范数优化的织物疵点分类研究
张五一,侯远韶,张继超,杨 扬
(中原工学院,郑州450007)
基于二维稀疏表示和范数优化的织物疵点分类研究
张五一,侯远韶,张继超,杨 扬
(中原工学院,郑州450007)
针对一维压缩采样丢失图像的结构信息,并带来识别精度损失的问题,提出了二维压缩采样的方法.利用一组稀疏基对疵点原始数据进行感知得到稀疏化数据,将织物疵点数据用二维稀疏表示,再利用范数优化的方法实现压缩数据的准确重建,根据稀疏基的不同得到织物疵点的不同分类.该方法解决了采集数据的泛滥和传感器的浪费,降低了计算的复杂度,有利于织物疵点的分类研究,进而为机器视觉识别织物疵点打下理论基础.
二维稀疏;织物疵点;范数优化;分类
在纺织产品中,织物疵点是影响布匹质量的主要因素,也影响着纺织品的价格.而帘子布作为一种特殊的纺织产品,其生产速度快,幅面大,表面纹理相对较为复杂,疵点种类多.所以,如何在复杂背景下快速检测帘子布疵点,对检测和识别技术提出了较高的要求.随着图像获取技术的不断发展,织物图像的采集已经得到了较好的解决,而找到行之有效的疵点检测识别算法,则成为研究的重点.然而,随着数据采集设备的完善和数据传感器处理能力的不断增强,图像的分辨率不断提高,图像识别要处理的数据维数也越来越多,而数据维数的提升使得实时完成图像处理和识别也越来越困难.为了解决数据维数提升带来的难题,需要为图像识别寻找减小数据冗余度的有效方法,完成原始数据的降维,以提高图像识别的速度.此外,图像的降维过程不仅要降低数据维数,还必须抓住图像的主要信息而忽略次要信息,因此图像降维还应是一种有效的特征提取手段.本文在一维压缩采样的基础上,提出了二维压缩采样的方法.这种方法充分利用了图像的结构信息,减少了数据的冗余和计算的复杂度,使机器视觉识别织物疵点的速度得到了提升.
1 二维稀疏表示的原理
图像分析的研究表明,基于机器视觉的图像识别可以归结为一个先提取特征然后再进行分类的过程.因此,织物疵点检测和识别本质上是一种将图像先提取特征然后再分类的问题.而近几年来,基于范数优化的稀疏表示理论的研究进展给我们带来了新的思路.该理论指出,若向量在某种变换下具有稀疏性(即向量的零元素项占多数),则可以利用这种稀疏性对该向量进行欠定的随机线性映射,而不必担心丢失任何信息.只要该欠定的映射矩阵满足一定的条件,就可以利用范数优化技术由这些“欠采样值”(采样频率低于经典的Nyquist频率)精确地重建原始向量.
对图像特征提取和分类算法的研究,传统上习惯从向量(一维)的角度出发,这种一维化的处理方法没有考虑图像的矩阵结构,因而往往带来较高的计算开销和识别的不稳定.
1.1 二维稀疏表示的意义
我们认为,将传统的一维特征表示和模式分类算法直接用于图像识别,将带来以下缺点:①丢失了图像的二维结构信息,在同等条件下使识别精度降低.②传统算法先将数据转化成向量形式,而这种“向量化”的手段将导致采样和重建过程中计算复杂度的提高.针对上述缺点,利用图像的矩阵结构(二维),可以完成一维方法向二维方法的扩展.扩展后的二维图像表示和分类算法在很大程度上解决了上述一维算法的缺点,并能够带动一维图像识别算法的升级和变革,从而对织物疵点检测与识别产生积极的影响.
1.2 从一维采样到二维稀疏采样
在介绍二维压缩采样之前,我们先将一维压缩采样概念作一下简单的介绍.设图像x为M×N的矩阵,将该矩阵转换为列向量x(vec)∈RM×N,则图像一维压缩采样形式的向量特征y(vec)∈RM(vec)可以通过下面的公式得到:其中,∅∈RM(vec)×(MN)(M(vec)<MN)为满足 RIP 条件的欠定随机矩阵(随机分布可取Gaussian分布).

在本研究中,如果我们不把x向量化,而是保持x∈RM×N的矩阵结构不变,并对公式(1)做一些改变,可以得到下面的二维压缩随机映射公式:
y=∅rx∅c(2)其中,∅r∈Rm×M,∅c∈Rn×N(m<M,n<N)分别为行采样矩阵(行映射)和列采样矩阵(列映射),∅r和∅c均满足RIP条件.和一维压缩采样不同,由公式(2)所得到的y不再是向量,而是一个矩阵(y∈RM×N).我们将矩阵y称为二维压缩采样测度.

公式(3)说明了矩阵y中的每一个元素均包含了行映射和列映射从矩阵x中抽取的一部分信息.
从理论上和实验上可以初步证明,只要x是分段光滑的(可以经过某个变换进行稀疏化),或者x本身就是一个稀疏矩阵,且矩阵y的行/列数大于某个确定的阈值(但小于x的行/列数),则y中包含的信息量就和x一样多,这样就可以使用凸化技术从y重建x.
在实际应用中,如果待采集的图像f本身不是稀疏的,但在某个Ψ基上的变换系数θ是稀疏的或者是可压缩的,那么图像f经过转换是可压缩的,即f=Ψθ.
稀疏表示理论不仅可用于特征表示,还可用于分类器的设计.例如,在图像识别中,假设输入的图像可以表示为训练集样本的线性和,且该线性和的系数向量是稀疏的,则通过稀疏向量中非零值的位置就可以对输入图像进行分类.而该过程实际上就是基于l1范数优化的稀疏向量重建过程[1-3].
1.3 二维稀疏的训练集表示
二维稀疏表示的思想还可以用图1来表示.
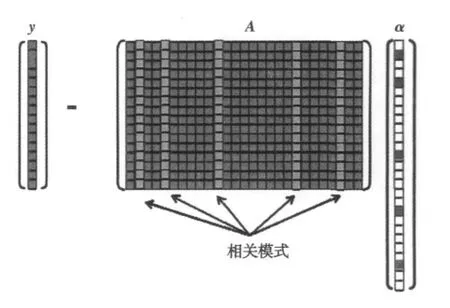
图1 基于稀疏表示的模式识别方法示意图
图1中字典A为训练集样本构成的欠定矩阵,其中各列为已知ID的模式向量,y为输入模式向量.当字典A中的样本足够充分时,则y可以表示为A中相关模式的线性和,此时系数向量α必为稀疏的,因此α中的非零值可以定位A中的相关向量,在此基础上可以确定y的分类,即如果A中的相关样本属于第i类的话,那么该图像也应被划为第i类.上述思想还可以用如下数学式来表示:
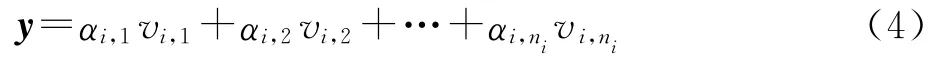
其中,Ai=[μi,1,μi,2,…,μi,n],为第i类训练样本集合;αi=[αi,1αi,2,…,αi,n]T,为系数向量[3].对于全体训练集样本(共k类)而言,公式(4)还可以写成如下的形式

其中,A=[A1,A2,…,Ak],为整个训练集;α=[α1,α1,…,αk]T,为系数向量.由于α仅与Ai有关,所以α必为稀疏向量,并且稀疏向量的位置和大小与Ai密切相关,通过对α的求解可以确定α的ID.
由于矩阵A为欠定矩阵,所以公式(5)中的α有无穷多组解.通过l1范数限制min‖α‖(α的最小l1范数),可以将上述问题转化为一个凸优化问题,从而得到α的稀疏解.上述思想被美国数学家Donoho D总结归纳为:“对于欠定线性方程组而言,其l1范数最小化的解通常也是欠定线性方程组的最稀疏解”[2].
2 二维稀疏表示的约束条件
通过香农采样定理可知,只有采样频率不小于奈奎斯特频率即模拟信号频谱中最高频率的2倍时,才能不失真地恢复原始信号.但是香农采样定理除了利用了信号是有限带宽的假设外,没有利用其他任何的先验信息,采集到的数据在很大程度上存在冗余性.二维稀疏表示并不是直接对数据进行采集,而是通过一组特定的波形去感知数据,即为了能够准确重建原始数据,必须用一组特定的波形去感知数据,并且要衡量特定波形与原始数据的相干程度,只有相干程度在可接受范围内时,才能利用范数优化的方法准确重建数据;涉及的关键因素在于给定的波形要与可以用来压缩原始数据的波形均不相干,并且不相干程度越高,感知数据包含的信息量就越大,那么准确获取重建原始数据所需的感知数据量就越少[4].国外提出的受限等距性原理、一致不确定性原理及准确重构原理,进一步回答了如何从压缩数据中方便地提取信号或者图像的有用信息问题[5].图2所示是采样过程的一个示意图,其中待采集信号f只在k个时刻非零(即为稀疏程度),并且只有在这k个非零时刻才能有效采集到信号f中的信息,并将其投影到给定的一组感知波形上(也可以说,用一组给定的波形对f进行感知),得到一组远小于数据原始长度的测量数据y[6].
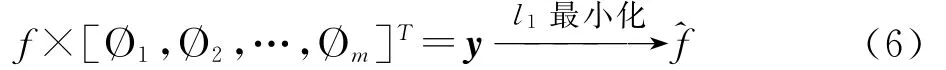

图2 压缩感知数据采集方式
2.1 相干性和稀疏性
2.1.1 不相干性
基与基之间的相干程度μ定义为:
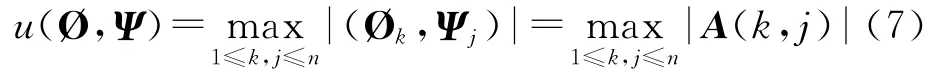
其中,∅k、Ψj分别是正交矩阵∅,Ψ的行向量和列向量(k,j分别表示矩阵的行和列).通过线性代数的知识可知,u所以当测度矩阵是单位矩时,相干程度u最大为1.在这种情况下,只有采集到和原始数据量相当的感知数据,才能估计出可压缩数据的重要信息.因此,当感知矩阵和变换矩阵之间的相干程度为1时,只能使用常规的采样方法.实际上,绝大部分矩阵之间都是不相干的,即相干程度都不为1.
相干程度最小的规范基是由傅里叶变换矩阵和脉冲函数∅k=δ(t-tk)形成的.脉冲函数 ∅k=δ(t-tk)与正弦曲线之间的相干程度为1/■n.
2.1.2 数据可压缩性
数据的可压缩性是指数据能够在较小损失的情况下通过较少的系数表达出来,或者数据在某个变换域的支撑域相对较小时是可压缩的.此外,当数据在空域或者某个变换域的系数属于lp球(0<p<1)时,数据也是可压缩的[7].此时,数据f在给定的Ψ 基下,由f=Ψθ确定的变换系数θ对任意给定的某一常数R(R>0)和p(0<p<1),满足

当系数θ属于lp球时,设θk是取θ中k个较大项,并将θ中的其他项置为零得到的向量,则

其中,ζ2,p是仅取决于p∈(0,2)的常数.因而为了使θk对θ的估计误差不大于ε,只需k≥ε(p-2)/2p,即最大的k个系数保留数据的大部分信息.
2.2 数据压缩与流形
数据的压缩可以解释为原始空间中稳定的流形嵌入,因此能有效地降低原始数据的维数,而不丢失信息.在此基础上对压缩数据进行学习和分类,等价于传统的学习和分类.例如,近年来提出的匹配滤波器算法就是对图像的压缩流形进行估计后再对目标进行识别和分类[8].类似的研究包括Davenport M等人对流形的随机映射所进行的分析,分析结果表明图像的压缩采样数据可用于检测、分类以及参数估计,其准确性类似于传统方法,但计算的复杂度却降低了.这些研究从流形嵌入的角度解释了图像压缩识别的有效性[9-13].
3 结 语
在本研究中,我们认为基于稀疏表示和范数优化的图像识别算法还可以继续改进.在稀疏变换和图像重建过程中,往往夹杂着噪声的干扰.如何在不影响图像重建的情况下最大限度地去除噪声,并利用图像的矩阵结构和稀疏基的不同对织物疵点图像进行准确重建和分类,还需要做以下改进工作:
(1)在数据压缩方面,目前所采用的测量矩阵大多为非确定性测量矩阵即随机矩阵,虽然它们在仿真实验中能够取得较好的效果,但是难以在硬件上实现.因而有必要研究自适应压缩技术,即根据不同的数据类型,采用不同的数据采样和图像重建策略[14].
(2)在稀疏表示方面,低秩表示和流形结构与数据稀疏性有着密切联系,如果将低秩表示和流形结构引入图像的稀疏表示中,将有望得到更好的压缩结果[15].
(3)在范数优化方面,如果能结合图像自身的稀疏性和先验性,那么图像的分类重建将会得到更好的恢复效果.
二维稀疏表示可以得到较低维数的数据,计算复杂度低,并且不依赖于训练集的选取,因此可以有效地用于数据的特征抽取.范数优化则可以精确地重建图像,有利于织物疵点的分类研究,进而为机器视觉识别织物疵点打下理论基础.
[1] Donoho D,Elad M.Optimal Sparse Representation in General(nonorthogonal)Dictionaries via L1 Minimization[C].New York:In Proceedings of the National Academy of Sciences,2003.
[2] Donoho D.For Most Large Underdetermined Systems of Linear Equations the Minimal 1-norm Solution is also the Sparsest Solution Comm[J].On Pure and Applied Math,2006,59(6):797-829.
[3] Wright J,Yang A,Ganesh A,et al.Robust Face Recognition via Sparse Representation[J].IEEE Transactions on Pattern A-nalysis and Machine Intelligence,2009,31(2):210-227.
[4] 戴琼海,付长军,季向阳.压缩感知研究[J].计算机学报,2011,34(3):425-434.
[5] Wright J.Robust Face Recognition via Sparse Representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(2):227-229.
[6] 焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J].电子学报,2011,39(7):1652-1657.
[7] Davenport M A.The Smashed Filter for Compressive Classification and Target Recognition[EB/OL].[2012-03-03].http://dsp.rice.edu/sites/dsp.rice.edu/files/cs/spie07-final.pdf.
[8] Duarte M.Multiscale Random Projections for Compressive Classification[C].Texas:IEEE on Image Processing(ICIP)2007.
[9] Wakin M B.Manifold-based Signal Recovery and Parameter Estimation[J].Compressive Measurements(Preprint),2008,22(3):226-231.
[10] PeyréG.Manifold Models for Signals and Images[J].Computer Vision and Image Understanding,2009,113(2):249-260.
[11] Baraniuk R G,Wakin M B.Random Projections of Smooth Manifolds[R].New York:Foundations of Computational Mathematics,2009:35.
[12] Hegde C M,Wakin R,Baraniuk.Random Projections for Manifold Learning[M].New York:Neural Information Processing Systems NIPS,2007:641-648.
[13] Davenport M.A Theoretical Analysis of Joint Manifolds(Technical Report TREE-0901)[J].Rice University ECE Department,2009,116(24):118-121.
[14] Yang J.Two-Dimensional PCA:A New Approach to Appearance-based Face Representation and Recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26(1):131-137.
[15] 杨平,施克仁.相控阵超声二维稀疏阵列的优化设计应用研究[J].应用声学,2008,27(2):148-150.
Study on a Fabric Defect Classification Based on Two-dimensional Sparse Representations and a Norm Optimization
ZHANG Wu-yi,HOU Yuan-shao,ZHANG Ji-chao,YANG Yang
(Zhongyuan University of Technology,Zhengzhou 450007,China)
As to sampling loss of the structural information of the image for the one-dimensional compression and the loss of recognition accuracy,a concept of two-dimensional compression samples is proposed.Using a set of sparse-based perception,the sparse data on the raw data of the defect,fabric defect two-dimensional sparse are gotten.Finally,using norm optimization method accurate reconstruction of the compressed data is realized,and different fabric defect classification is gotten.This approach solves the proliferation of data collection and the sensor waste and greatly reduces the computational complexity,fabric defect classification,and thus to lay a theoretical foundation for machine vision to identify fabric defects.
two-dimensional sparse;fabric defects;norm optimization;classification
TP391.4
A
10.3969/j.issn.1671-6906.2012.03.005
1671-6906(2012)03-0024-05
2012-03-08
河南省科技攻关计划项目(0721002210032)
张五一(1955-),男,河南洛阳人,教授.

