微波成像技术及其算法综述

许 会，陈艳玲

（沈阳工业大学 先进在线检测技术省重点实验室，沈阳 110870）

近些年来，微波成像理论在科学、技术方面的重要作用已经受到越来越多的关注。微波成像技术以微波在各种复杂媒质中的传播和散射的研究为基础，从待测目标的散射场反演目标的几何形状、空间位置、电磁特性等参数。微波成像技术作为电磁逆散射技术的重要内容，可实现对目标的无损检测，能同时对目标进行几何成像和物理成像，且具有较高的分辨率，因而微波成像技术在地球物理探测、生物医学成像、环境监测等领域具有重要用途［1－2］。但是由于背景介质复杂、未知量大以及反演过程病态等问题，该项研究一直是电磁学领域的重要课题。笔者阅读了近5年来的80余篇国内外的文献，发现其中针对微波成像细节方面，如参数估计方法、测量方案、优化准则等研究［3］的文献占了总数的10%；算法研究［4－14］的文献将近占据了40%；微波成像的应用方面的文献则占据50%左右，尤其是在生物医学成像方面如对乳腺癌的检测等应用方面的文献有着很大的比重［15－16］。尽管应用于实践是理论研究的最终目的，但是逆算法作为微波成像的重要内容，起着关键的作用。文章针对微波成像算法问题进行讨论，对现存的微波成像算法做了简要的概述，并对几种具有代表性的成像算法的原理、特点及使用范围进行介绍。

微波成像技术的主要任务是求解微波照射被测媒质时的逆散射问题，通过测量被测媒质外部的散射场数据，重建被测媒质内部的复介电常数图像。被测的散射场携带大量有关散射体的信息，利用关于散射目标的先验知识，经过适当的数学处理之后可以提取出散射体本身所具有的某些特性，如散射体的形状、介电常数的分布等。微波成像技术一般包含两部分：一部分是正演数值模拟，即计算给定模型的电磁场分布；另一部分是逆过程，即根据给定的测量场重构电参数的分布［1－4］。此技术可以检测非金属或金属材料内部缺陷的大小、形状、位置以及物理检测化学变化过程，在物体的无损伤性检测其内部缺陷的应用中能起很大的作用。过去的几十年里，在微波成像和电磁逆散射技术的相关领域内应用逆算法在效率、鲁棒性、有效性方面取得了很大的进展。

对于微波成像中正问题的求解可使用解析法或数值法进行，其中解析法仅适用于少数典型物体的散射场的计算，而数值法可计算复杂形状物体的散射。而对于逆问题，许多的算法被用来反演测得的散射数据。根据不同算法的特点，有三种分类方式［5－8］，如表1所示。下面对电磁逆散射的图像重建问题进行讨论，介绍几种具有代表性的成像算法。

1 ω－k算法

ω－k算法［10］是一种典型的谱域重建算法。与传统的合成孔径成像算法相比，该算法具有更高的精度和计算速度，适用于均匀散射背景下的成像，如飞机降落时对不明物体的侦查、对宽测绘带星载SAR数据进行精确成像处理等。ω－k算法公式为：

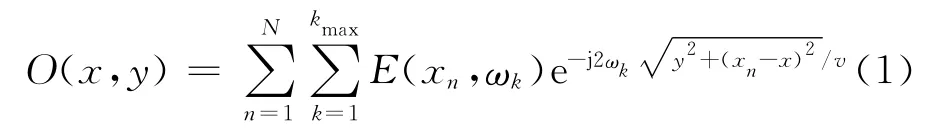
式中E（xn，ωk）表示在测试点xn处，频率为ωk时的电场值，其中n＝1，2，3…，N，k＝1，2，3…，kmax；O（x，y）为目标物体函数，（x，y）为成像点的坐标；v为波在介质中传播的速度。

ω－k算法流程如图1所示。算法步骤如下：

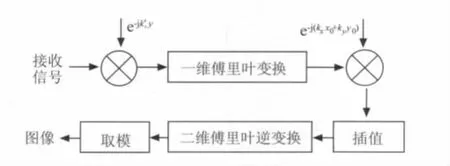
图1 ω－k算法流程框图

（2）作Y方向一维傅里叶变换。

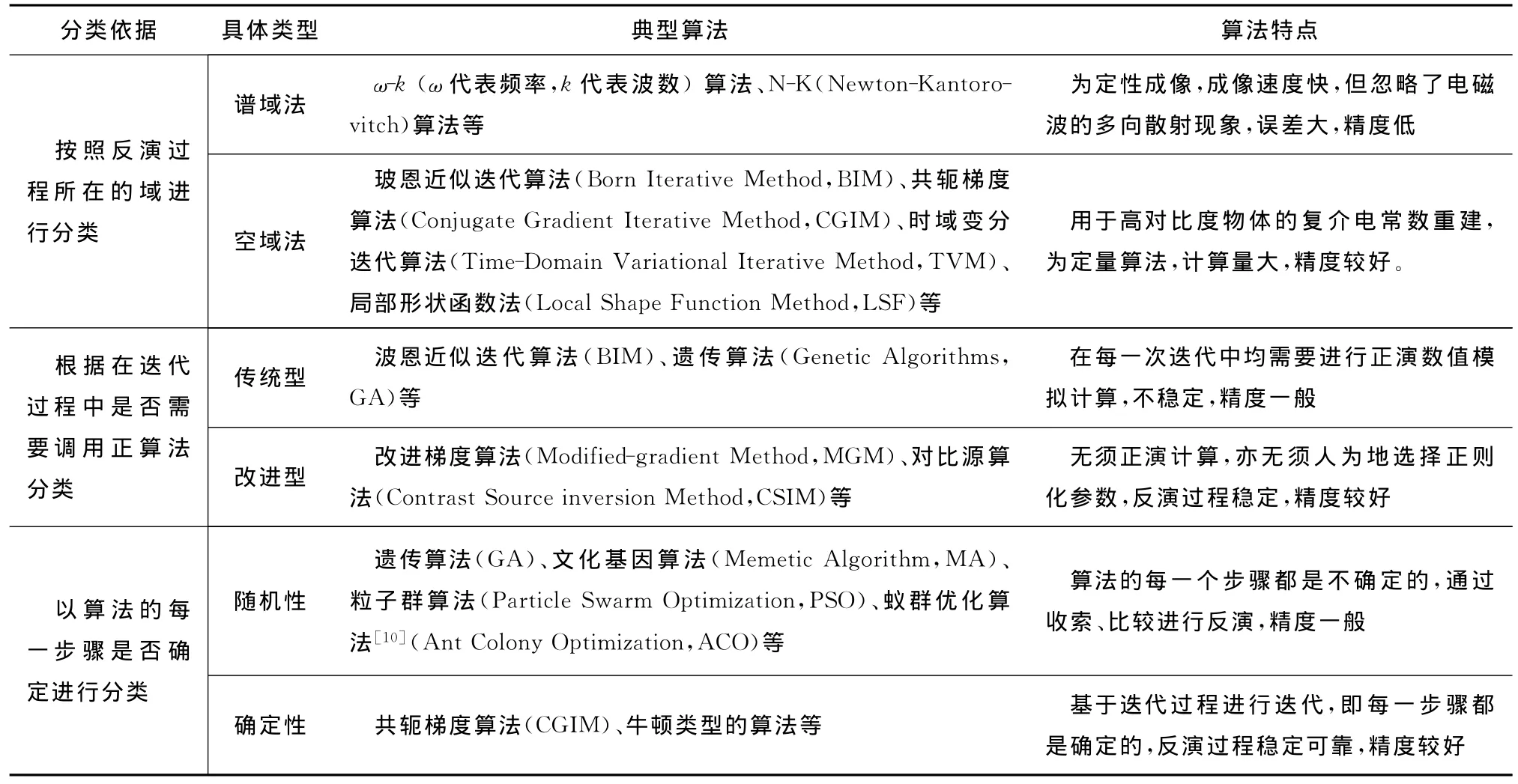
表1 微波成像算法分类列表

（3）进行空间移位、插值等处理，其中（x0，y0）为目标的中心坐标。

（4）将处理过的信号作二维傅里叶反变换，得到的幅度为空间分布图像。

（5）对反变换后的矩阵中的复数数据元素逐个取模。

2 局部形状函数算法

局部形状函数算法［11］（LSF）是一种典型的空间域非线性迭代算法。LSF是一种充分的、一般的方法，可用于包含多个强散射体和任意形状、大小的散射体的情况。由于该方法原理简单，适用于强散射体的成像，故多被用来对金属散射目标进行重建。但散射矩阵T的求取也成为该算法的一个难点。

如图2所示，LSF方法是通过将散射问题转化成求解二进制函数问题来将非线性问题线性化。散射区域V被离散化为N 个单元，每一单元用Vi表示，i＝1，2，3…，N。假设子区域Vi划分的足够小且每一单元Vi里具有相同的介电常数和电导率，S为金属散射体所在的区域。

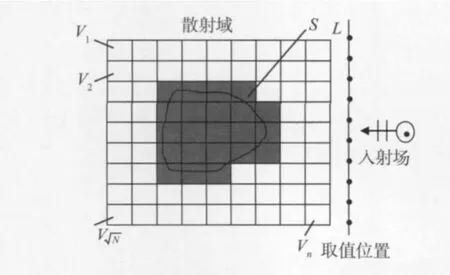
图2 LSF算法的二维散射模型

则二进制形状函数γi如下所示：

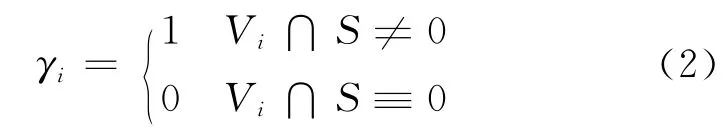
这里假定γi为二进制变量，取值为0或1，含有金属散射体的区域的形状函数设为1，不含金属散射体的区域的形状函数设为0。但是在实际迭代和求解最优值时，需要将γi设定为一个在0到1之间连续变化的变量，然后通过逆算法得出关于γi的图像。则LSF算法的重建步骤如下：

（1）对参数设置初值。求取散射域内的已知的总场分布，得到目标物体函数γi的分布作为初始分布，或者假设初始值由其它先验知识提供。

（2）求解重建的目标函数，可以用矩量法或其它算法如时域有限差分法（FDTD）进行正向问题的计算，得到检测域和成像域的总场分布。

（3）比较由重建的目标函数得到的检测场分布和实际的检测场分布，若两者相当接近，低于某种准则所规定的误差可停止迭代过程，否则，用新的计算结果更新成像域分布，重新迭代至满足误差限。

（4）重建二进制形状函数γi来构建散射体图像。

3 波恩近似迭代算法

波恩近似迭代算法［12］（BIM）属于一种典型的传统型的空间域非线性迭代算法。此算法在每一次迭代中均需进行正演数值模拟计算和线性化过程，适用于对电介质和导电媒质目标的重建。当被测媒质介电常数与背景介质的介电常数相比差别不大于10∶1的时候，可以利用波恩近似来简化逆散射问题，不适用于对强散射体成像的计算且反演速度较慢，精度低。变形波恩迭代法（DBIM）是对BIM的改进。与BIM相比，DBIM收敛快，但抗随机噪声的能力低，数值实现不方便，只适用于小尺寸、低对比度目标的反演，且精度不高。

设入射场为单位TM波，则电磁散射方程为：

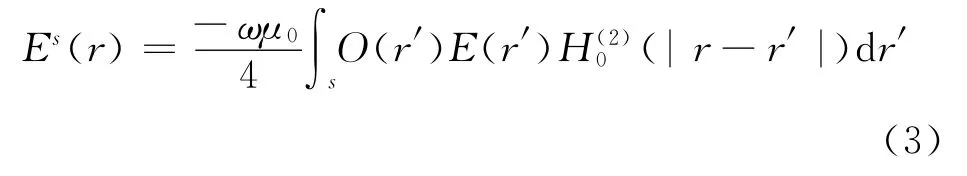
式中ω为角频率；μ0为自由空间的磁导率；r＝（x，y）为场点；r′为源点；O（r′）为目标函数；为0阶第二类Hankel函数。Es为散射场，总场为入射场和散射场之和，如式（4）所示：

式中Ei为入射场，E为总场。将式（4）代入式（3），得：

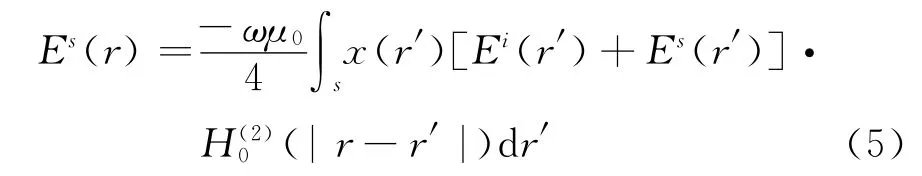
从上面过程中得到波恩近似迭代法的反演方程。

4 对比源算法

对比源反演算法［6－7］（CSIM）是一种典型的改进型算法，将反演问题转化为求解成本泛函的极小值问题，从而形成重构对比源和对比度的迭代序列。该算法由于无须正演计算，亦无须人为地选择正则化参数，所以反演过程稳定，适用于均匀背景介质和层状背景介质中。乘法正则化－对比源算法［7］（multiplicative regularized contrast source inversion method，MR－CSIM）是在CSIM上的改进，能够得到更好的分辨率和精确度。

在图3的散射模型中，S为散射体所在的区域，T为成像区域，V为散射区域。若用E表示总场，Ei表示入射场，Es表示散射场，则总场可以如式（4）所示。

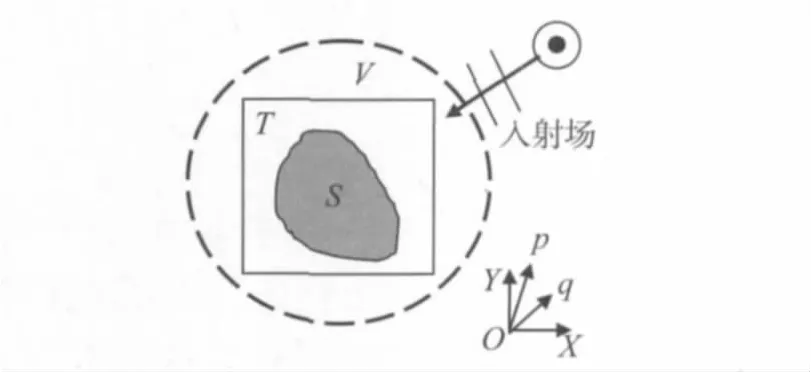
图3 CSIM法的二维散射模型

设p，q为X－Y 平面内的位置向量（x，y），n代表发射源的序号（因为在逆散射的测量中需要多个发射源），背景的复介电常数为εb，则电参数对比度χ可以写为式（6），对比源w则如式（7）所示。

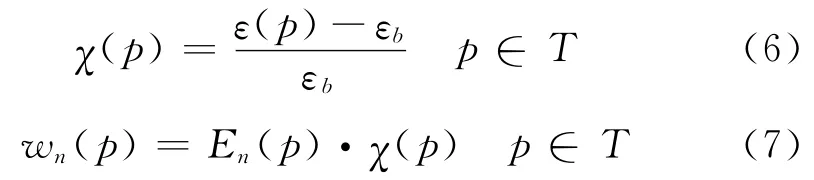
则该算法成本泛函的数据方程和目标方程的线性组合为：

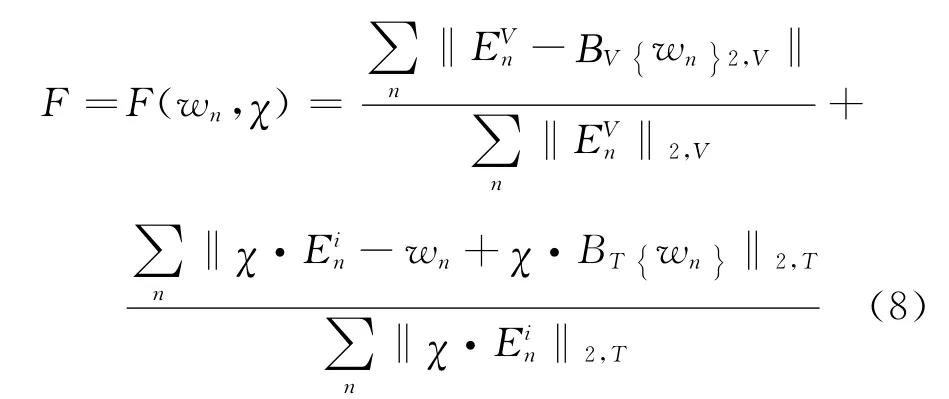
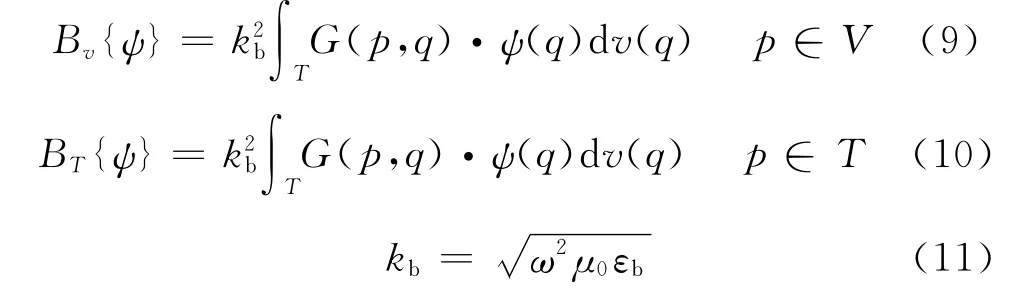
式中ω为角频率；μ0为自由空间的磁导率；G（p，q）为关于背景介质的格林函数。

式（8）中右侧第一项为度量数据方程的归一化误差，第二项为度量目标方程的归一化误差。当wn＝0时，这两项均为1，且因为目标方程的约束，CSIM反演问题的解的非惟一性大大降低。分别对对比源wn和电参数对比度χ进行更新，轮流依次迭代，可以实现对式（8）的极小化。

5 粒子群优化算法

粒子群优化算法［13］（PSO）是一种启发式全局优化技术，一种基于群智能的进化计算技术，由Eberhart博士和Kennedy博士发明，源于对鸟群捕食的行为研究。PSO同遗传算法类似，是一种基于迭代的优化工具。系统初始化为一组随机解，通过迭代搜寻最优值。但是并没有遗传算法用的交叉以及变异。通过利用个体间的协作和竞争来实现对问题最优解的搜索。PSO的优势在于简单容易实现，采用实数求解并且需要调整的参数较少，是一种通用的全局搜索算法。

PSO初始化为一群随机粒子（随机解），然后通过迭代找到最优解。假设在一个D维的搜索空间中，随机初始化m个粒子组成一个群落，其中第j个粒子的空间位置为xj＝（xj1，xj2，…，xjD），j＝1，2，…，m。每个粒子在搜索空间中以一定的速度飞行，速度定义为vj＝（vj1，vj2，…，vjD），可根据经验进行动态调整。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，记为gj＝（gj1，gj2，…，gjD），这个解叫做个体极值，另一个极值是整个种群目前找到的最优解，记为zj＝（zj1，zj2，…，zjD），这个极值是全局极值。在找到两个极值时，粒子可根据如下的迭代公式来更新自己的速度和位置。

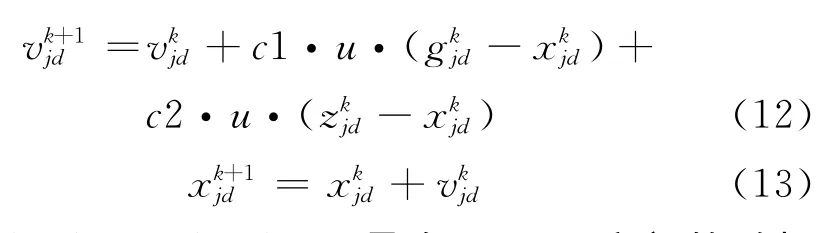
式中1≤j≤m；1≤d≤D；u是介于0～1之间的随机数；c1，c2是学习因子，通常c1＝c2＝2。每一维粒子的速度都会被限制在一个最大速度vmax内，当vmax较大时，粒子飞行速度大，有利于全局搜索，但有可能错过最优解；当vmax较小时，粒子在特定区域内精细搜索，但容易陷入局部最优。PSO的算法流程如图4所示。

6 非精确牛顿算法

非精确牛顿算法［14］（Inexact Netwon Method，INM）是一种典型的确定性算法，由两个嵌套的循环组成。外面的循环是使非线性散射方程线性化，里面的循环则是运用截断的Landweber算法求解已经被线性化了的方程。该算法适用于包含强散射体的电磁逆散射问题。该算法的迭代步骤为：

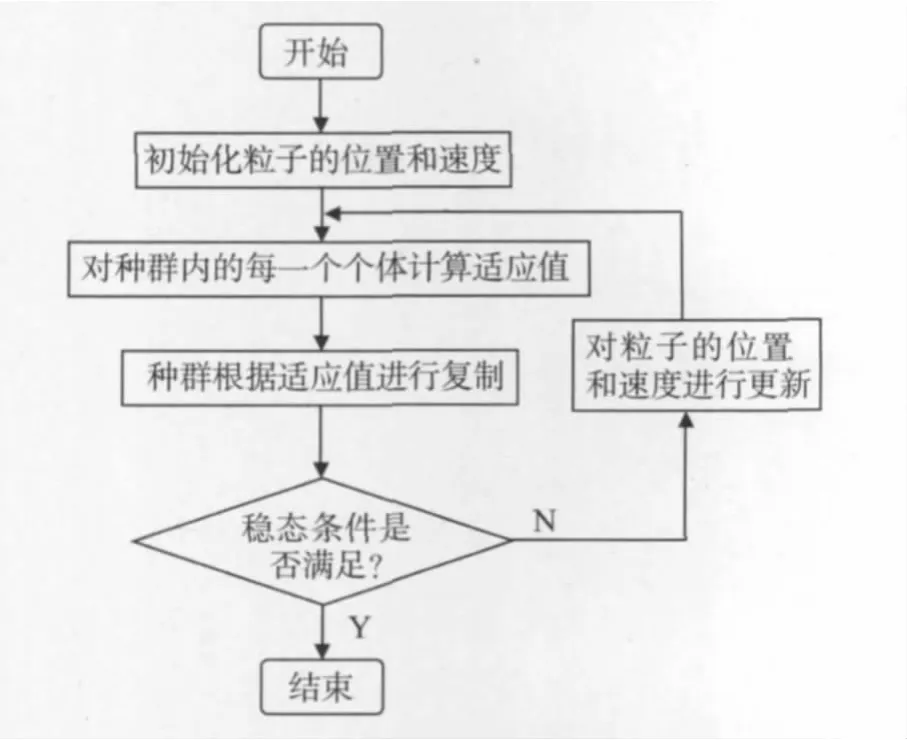
图4 PSO算法的流程图

（1）给定初始值x0，置n＝0。

（2）通过计算Fre′chet导数，进行线性化，从而得到线性方程。

（3）运用截断的Landweber算法，进行正则化操作，计算有限的序列hn。

（4）通过设置xn＋1＝xn＋hn来更新数据，且n＝n＋1。

（5）若║xn＋1－xn║≤δ，δ为终止条件，则迭代终止。否则，置n＝n＋1，转到步骤（2）继续进行迭代。

7 结论

除了上述介绍的方法外，微波成像还有很多算法，并且不断有新算法提出。随着人们对实际问题的重视和研究的深入，智能算法开始越来越多地应用于微波成像问题中，一系列的混合算法也被提出，如牛顿算法与对比源算法相结合、线性采样方法与蚁群优化算法相结合等。同时，研究人员也开始把目光更多地关注于实际数据的重构。在未来时期内，智能算法和混合算法将成为解决微波成像问题的主流算法，微波成像技术的研究将不断得到完善，其应用也将更加广泛。

［1］Hu G H，Qu F L，Zhang B.Direct and inverse problems for electromagnetic scattering by a doubly periodic structure with a partially coated dielectric［J］.Mathematical Methods in the Applied Sciences，2010，33（2）：147－156.

［2］Cakoni F.Recent developments in the qualitative approach to inverse electromagnetic scattering theory［J］.Journal of Computational and Applied Mathematics，2007，204（2）：242－255.

［3］Winters D W，Van Veen B D，Hagness S C.A sparsity regularization approach to the electromagnetic inverse scattering problem［J］.IEEE Transactions on Antennas and Propagation，2010，58（1）：145－154.

［4］YU Chun，YUAN Meng－qing，ZHANG Yang－jun，et al.Microwave imaging in layered Media：3－D image reconstruction from experimental data［J］.IEEE Transactions on Antennas and Propagation，2010，58（2）：440－448.

［5］Dubois A，Belkebir K，Catapano I，et al.Iterative solution of the electromagnetic inverse scattering problem from the transient scattered field［J］.Radio Science，2009，44（1）：199－201.

［6］Gilmore C，Mojabi P，Lovetri J.Comparison of an enhanced distorted born iterative method and the multiplicative－regularized contrast source inversion method［J］.IEEE Transactions on Antennas and Propagation，2009，57（8）：2341－2351.

［7］Bozza G，Pastorino M.An inexact newton－based approach to microwave imaging with in the contrast source formulation［J］.IEEE Transactions on Antennas and Propagation，2009，57（4）：1122－1132.

［8］Pastorino M.Stochastic optimization methods applied to microwave imaging：areview［J］.IEEE Transactions on Antennas and Propagation，2007，55（3）：538－548.

［9］Brignone M，Bozza G，Randazzo A，et al.A hybrid approach to 3Dmicrowave imaging by using linear sampling and ACO［J］.IEEE Transactions on Antennas and Propagation，2008，56（10）：3224－3232.

［10］Cadalli N，Munson D C.A simulation study of theωk SAR algorithm squinted case with application to runway imaging［C］.Proceedings of the IEEE Interational Conference on Application Specific Standard Product.Istanbul，Turkey：2000.

［11］Weedon W H，Chew W C.Time domain inverse scattering using the local shape function（LSF）method［J］.Inverse Problems，1993，（9）：551－564.

［12］Moghaddam M，Chew W C.Comparison of the born iterative method and tarantola's method for an electromagnetic time－domain inverse problem［J］.Interational Journal of Imaging Systems and Technology，1994（3）：318－333.

［13］Donelli M.，Franceschini G.，Martini A.，et al.An integrated multiscaling strategy based on a particle swarm algorithm for inverse scattering problems［J］.IEEE Transactions on Geoscience and Remote Sensing，2006，44（2）：298－311.

［14］Bozza G，Estatico C，Pastorino M，et al.An inexact newton method for microwave reconstruction of strong scatterers［J］.IEEE Antennas and Wireless Propagation Letters，2006，5（1）：61－64.

［15］Golnabi A H，Meaney P M，Geimer S，et al.Micro－wave Imaging for Breast Cancer Detection and Therapy Monitoring［C］.IEEE Topical Conference on Biomedical Wireless Technologies，Networks，and Sensing Systems.Phoenix，Arizona，USA，2011.

［16］Ashtari A.Using apriori information for regularization in breast microwave image reconstruction［J］.IEEE Transactions on Biomedical Engineering，2010，57（9）：2197－2208.