基于自抗扰控制的变速非圆车削技术研究*

曹 辉 张 娜 梁 宁

(①西南科技大学制造科学与工程学院，四川绵阳 621010;②四川工商职业技术学院，四川成都 611830)

非圆截面零件在机械、光电产品中得到了大量应用，内燃机活塞、凸轮轴、盘形凸轮等都是典型的非圆截面。非圆截面的加工一直是个难题。传统加工非圆截面工件采用铣削或磨削加工，这些加工方法周期长、精度低、成本高、效率低、柔性差。非圆截面车削加工是实现非圆截面零件快速、高精度、高效加工的有效方法。该方法的加工原理是，主轴编码器实时跟踪主轴转角位置，并将该位置信息反馈给数控系统，数控系统根据程序设定的轨迹，驱动刀具移动至指定的目标并进行闭环控制，从而加工出所需的非圆截面。在此过程中，系统的关键是快速刀具进给伺服系统(Fasting Tool Servo，简称FTS)，该系统驱动刀具做往复运动，完成工件轮廓加工，它的性能决定了非圆截面加工精度和质量。

随着工件轮廓精度要求的提高，对非圆截面车削系统提出了更高的要求，FTS的跟踪精度和响应速度成为关键。由于FTS受数控系统控制，其执行机构总有一定的响应时间，因此，刀具不可避免地产生相对于目标位置的偏移。刀具的实际运动轨迹表现为低频理想振动和高频噪声振动的叠加。高频噪声振动反映了非圆车削过程的稳定性，其幅度直接影响了非圆工件截面轮廓的尺寸精度。要提高非圆截面工件的加工精度，就是要提高非圆车削稳定性，降低高频噪声振动幅度［1－2］。

提高非圆车削系统的稳定性，首先要优化FTS的结构，提高系统的动刚度，减小响应误差。其次，对于优化后的FTS系统，要进一步提高系统加工过程中的稳定性，利用变速加工(Variable Spindle Speed Machining，VSM)是行之有效的解决方法。

变速加工是指人为地以各种方式改变主轴转速所进行的切削方式，在变速过程中，主轴在一个基本转速上以一定频率和幅度做连续的周期性变化。变速加工的概念是德国Stoferle教授于1972年最早提出并用来改善车削加工的稳定性。在变速加工研究方面，主要通过机理和应用两个方面，首先建立运动数学模型，通过时域、频域等分析方法，研究变速加工在抑制振动、提高稳定性方面的原因，并通过仿真、实验方法来验证结论的正确性［3－5］。

由于变速加工可以提高加工稳定性，因此，本文将变速加工引入非圆车削系统中，提高非圆截面工件轮廓加工精度。设计了非圆截面变速车削系统结构，将自抗扰控制方法运用于刀具高速驱动机构控制中，设计一种基于PMAC的数控车床控制系统，实现主轴与刀具高频往复运动的协调控制。

1 非圆截面车削结构设计

非圆截面车削过程中，随着工件转角的不同，刀具切削的前角、后角也不同，如图1所示。

设刀具在背平面内的前角为零，在加工图示非圆截面工件时，刀具的前角变化范围为±θ，θ角等于工件加工处轮廓曲线压力角。在切削加工中为了得到恒定的前角，刀具在高频移动的同时还应做摆动运动。图2是基于以上考虑设计的一种具有复合运动的刀具驱动装置示意图，详细设计见参考文献［6］。

变速非圆截面车削系统结构如图3所示，该系统包括普通数控车削单元和高频响应刀具驱动单元。普通数控车削单元完成主轴转速控制、主轴转角测量、Z向进给控制等功能，分别采用交流异步电动机、旋转编码器和交流伺服电动机。数控系统采用PMAC可编程多轴运动控制器，PMAC可编程多轴运动控制器采用Motorola的DSP56001为CPU;高频响刀具驱动单元驱动刀具按照程序设定的轨迹完成加工及刀具加工角度调整等功能。

上位机发出主轴变速信号，通过PMAC生成所需参考信号并将该信号输出至矢量变频器，矢量变频器驱动交流异步电动机输出可连续调节的主轴转速。交流异步电动机通过相应机械传动机构驱动机床实现所需的主轴变速运动。实际的主轴转速通过编码器反馈至PMAC实现闭环速度矢量控制。

2 主轴变速特性描述

在变速非圆截面车削过程中，主轴转速在一个基本转速上周期性变化，变化规律可用相关函数来表达。Insperger［7］等人研究了不同形式的主轴转速变化规律，总结出按正弦函数形式变化的主轴转速最优，即主轴转速变化规律为

该式的无量纲表达式为

式中:ωn为主轴的基本角速度;A为角速度变化幅值;f为角速度变化频率;t为时间变量;φ为角速度变化的初始相位角;RVA=A/ωn为速度变化的相对幅度;RVF=2πf/ωn为速度变化的相对频率。

研究表明，增大RVA、RVF值可以减小变速加工振动，提高系统稳定性。但由于变速加工系统条件限制，RVA、RVF只在允许的参数范围内变化。

3 快速刀具伺服系统设计

3.1 直线电动机模型

根据直线电动机工作原理和机械结构，可将其简化为一弹簧质量系统［6］，但切削力是随时间变化的，整个系统是一时变系统，系统动力学方程为

式中:m为运动部件质量;c为系统阻尼系数;k为弹簧刚度系数;x为电动机轴位移;Fa为直线电动机驱动力;Fd为外界阻力(主要是切削力);t为时间变量。

由式(3)可得系统的传递函数为

该系统为典型二阶系统，传递函数可采用实验方法测定。

3.2 直线电动机控制方法

在变速非圆截面车削过程中，主轴转速要求周期性变化，FTS跟踪主轴位置而做径向往复跟踪运动。主轴的位置通过主轴编码器进行测量，主轴转速的周期性变化导致编码器采样间隔是周期性时变的。这使FTS的跟踪控制更为复杂。Tsao and Pong［8］等人将周期性时变的采样间隔转换为主轴旋转角度作为变量来解决FTS的控制问题。由于旋转角度由旋转编码器测量，而编码器采样的角度间隔是常数，不随旋转速度变化而变化。这样可将时变的采样间隔转换为角度域变量。由此，直线电动机动力学方程变为

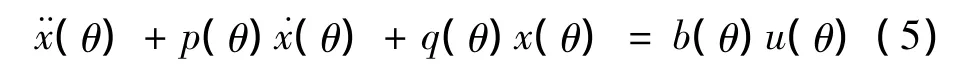
式中:x为电动机轴位移;u(θ)为角度控制信号;p(θ)、q(θ)、b(θ)为周期系数。

在控制系统设计时，要使系统具有较高的抗干扰性能，同时要使跟踪误差降到最小，满足机床适用性能。为此，将自抗扰控制(ADRC)技术应用于本系统控制中。

由方程(5)可知系统动力学方程的解可写为

其中:b0为b的近似值，w为系统输入力。文献［9］给出了如图4所示自抗扰控制技术结构图。图中微分跟踪器(TD)的作用是安排过渡过程并给出此过程的微分信号，扩张状态观测器(ESO)给出对象状态变量的估计z1(t)、z2(t)以及扰动的实时作用量a(t)=f(x，˙x，ω，θ，w)的估计z3(t)，而z3(t)/b0的反馈将起补偿扰动作用，这是一个具有自动补偿系统扰动的反馈结构。实际上，这个结构中控制量被分成两部分，即

其中:z3(t)/b0是补偿扰动的分量，而u0(t)是用状态误差ε1、ε2的非线性反馈来控制积分器串联型的分量。用控制律式(7)进行控制称为用b0u来实现自抗扰控制。

4 变速非圆截面车削系统稳定性及实验分析

4.1 系统稳定性分析

变速非圆截面数控车削系统是周期性时变系统，加工系统主振频率f随机床主轴转速n呈分段线性锯齿状变化［1］，切削过程将随机床主轴转速n的周期变化在条件稳定区和不稳定区交替进行，这种切削状况扰动了再生颤振的持续进行。当切削过程在条件稳定区进行时，机床加工系统的振动响应趋于零。另一方面，在非稳定区，刀具噪声振动是一种变频激励响应，其幅值要小于恒速车削时固定频率激励下的响应。这就使得变速加工可以有效地降低非圆车削时的刀具噪声振动，从而提高非圆车削稳定性。

4.2 系统实验分析分析

利用该车床对某凸轮试件进行车削实验，实验对象和方法与文献［6］相同，其中变速非圆截面车削参数ωn=62.8 rad/s，RAV=0.2，RAF=0.05，为了与恒速非圆截面车削结果进行对比，特将两种实验结果列于表1。

表1 实验跟踪误差 μm

从表1可看出，采用变速非圆截面车削方法较恒速加工方法显著提高了凸轮截面跟踪精度，减小了跟踪误差，提高了表面加工质量。

5 结语

应用自抗扰控制技术和角度域编程方法，将变速加工应用于非圆截面车削加工中，能够抑制加工过程中的自给振动，提高加工过程中的稳定性。通过实验验证，可得到以下结论:

(1)基于自抗扰控制的直线伺服单元具有良好的跟踪性和鲁棒性，能够满足非圆车削的精度要求。

(2)变速非圆截面加工较恒速非圆截面加工显著提高了加工精度，减小了跟踪误差，提高了加工系统稳定性，抑制了加工过程中的自给振动。

(3)选择正弦函数作为变速加工主轴驱动函数，实现该驱动方式简单、可靠，选择合适的RVA/RVF参数能够优化非圆截面工件加工质量。

［1］于骏一，杨辅伦，吴博达.变速切削方法的减振原理［J］.机械工程学报，1995，31(6):11 －16.

［2］WU Dan，WANG Xiankui，ZHAO Tong.Profile precision analysis and enhancement for noncircular turning［A］.Proceedings of the Second International Conference on Precision Engineering and Nano Technology［C］，Changsha:P.R.China Oct.，2002:265 －270.

［3］SEXTON J S，STONE B J.The stability of machining with continuously varying spindle speed［C］.CIRP Annual Manufacture Technology，1978，27:321－326.

［4］WU D，CHEN K，WANG X.Tracking control and active disturbance rejection with application to noncircular machining［J］.International Journal of Machine Tools and Manufacture，2007，47(15):2207 －2217.

［5］HANSON R D，TSAO T C.Periodic sampling interval repetitive control and its application to variable spindle speed noncircular turning process［J］.Journal of Dynamic Systems Measurement and Control—Transactions of the ASME，2000，122(3):560 －566.

［6］INSPERGER T，STEPAN G.Stability analysis of turning with periodic spindle speed modulation via semidiscretization［J］.Journal of Vibration Control，2004(10):1835 －1855.

［7］TSAO T C，PONG K C.Control of radial runout in multi－tooth face milling［C］.North American Manufacturing Research Conference，1991，9:183 －190.

［8］韩京清.从PID技术到自抗扰控制技术［J］.控制工程.2002，9(3):13－18.

［9］曹辉，李双跃.基于自抗扰控制的非圆截面数控车削［J］.机械设计与研究，2011，27(1):77 －79.