数控机床静刚度有限元分析*

刘启伟 王海滨 朱春雨

(①沈阳机床(集团)有限责任公司，辽宁沈阳 110142;②沈阳铁路机械学校，辽宁沈阳 110036)

机床的静刚度是指在切削力或其他外力作用下抵抗变形的能力，亦指刀具和工件间的刚度［1］。数控机床比普通机床要求具有更高的静刚度和动态特性，有标准规定数控机床的刚度系数应比类似的普通机床高50%左右。

分析材料和结构的刚度是工程设计中的一项重要工作，对于一些须严格限制变形的结构(如床身、主轴、刀架等)，须通过刚度分析来控制变形，许多结构也要通过控制刚度以防止发生共振、颤振或失稳。对于具有复杂结构的装配体来说，其工艺系统的静刚度不仅要考虑各个零件的材料属性，还要将装配方式和结合面特性包含进来，因此提高了分析的难度。国内外对装配结构的分析和研究工作广泛，有针对结合面参数识别和建模方法研究的［2－3］，有针对关键部件进行分析的［4－7］，也有进行整机建模分析的［8－9］。

现代加工条件需求的变化和科学技术的不断发展，使数控机床愈来愈向高速、高精度、高强度的方向发展，如何保证和提高机床的刚度是设计人员需要面对的问题。本文通过静刚度试验和有限元分析技术，结合数控机床串联刚度场理论，分析了数控车床的整体静刚度和各个部件对整机的刚度影响情况，对机床的性能分析和结构优化具有很好的参考价值。

1 机床结构分析

本文试验及分析的对象为沈阳机床集团某数控车床，机床为采用水平床身配上倾斜放置的滑板的卧式数控车床，机床的主轴驱动系统采用无级调速主电动机经皮带轮降速后传给机床主轴。图1是机床装配结构图。

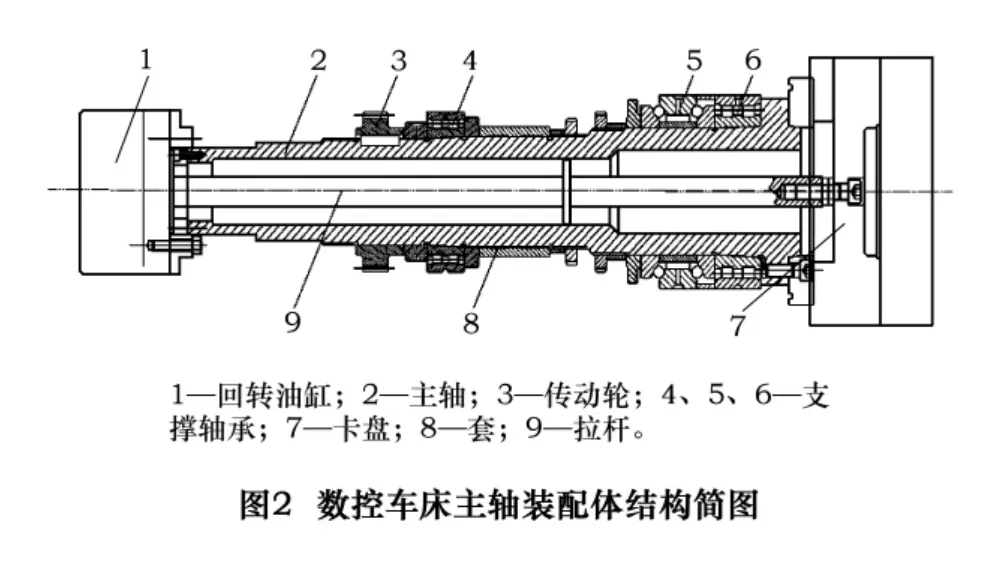
图2是机床主轴的装配示意图。主轴有前后2个支撑，前支承由1个双列圆柱滚子轴承6和1对角接触球轴承5组成，轴承6用来承受径向载荷，两个角接触球轴承背对背安装，用来承受双向的轴向载荷和径向载荷。主轴的后支承为双列圆柱滚子轴承4，主轴的支承形式为前端轴向固定、后端轴向放开，主轴受热膨胀向后伸长。前后支承所用圆锥孔双列圆柱滚子轴承的支承刚性好，允许的极限转速高。前支承中的角接触球轴承能承受较大的轴向载荷，且允许的极限转速高。

2 整机有限元分析

2.1 建立有限元模型

结构静态分析是有限元分析中最基本的分析类型，但对于装配体来说仍然存在很多问题需要解决，如模型的简化程度、结合面的处理方式、轴承和导轨刚度的等效简化等。一般而言，在模型简化、建立有限元模型时，应遵循等效刚度原则，即简化后的模型和原模型在刚度上应基本保持一致。由于机床装配体各部件间的结合面对机床性能影响很大，尤其是导轨结合面和大件间的螺栓固定结合面，研究表明，机床总柔度的40% ～60%是结合面产生的［10］，因此，在建立有限元模型时必须考虑结合面特性，建立这些结合面的等效模型。

此外，主轴轴承的刚度对主轴的受力变形影响很大，其刚度可通过轴承样本查询或采用公式法计算［11］;驱动丝杠系统对其轴向驱动部件有拉伸控制作用，其刚度也应予以考虑。图3为简化后划分网格的有限元模型。

2.2 X向静刚度分析

分别在主轴和刀架、尾台和刀架上沿X轴方向施加一大小相等、方向相反的力，计算上述2种受力情况下机床变形情况。从分析结果可以计算出各个部件的静刚度，其中主轴静刚度为67.5 N/μm，刀架静刚度为89.2 N/μm，尾台静刚度为87.7 N/μm，X向综合静刚度为38.4 N/μm。图4和图5为机床变形图。

2.3 Z向静刚度分析

分别在主轴和刀架上沿Z轴方向施加一大小相等、方向相反的力，计算机床变形情况，并计算机床Z向静刚度。计算结果:主轴静刚度为179.5 N/μm，刀架静刚度为93.9 N/μm，综合静刚度为61.7 N/μm。图6是机床变形云图。

3 静刚度测试

数控车床静刚度测试包括主轴X向和Z向静刚度测试、刀架X向和Z向静刚度测试、尾台X向静刚度测试、机床X向综合静刚度和Z向综合静刚度测试。试验包括加载和卸载2部分，每次试验重复2次，最后取平均值。以机床综合静刚度测试为例，通过施加在卡持在主轴上的圆棒的力以及利用固定在刀架上的千分表检测出主轴头位移，即可计算出机床X向综合静刚度，其试验原理图见图7示。

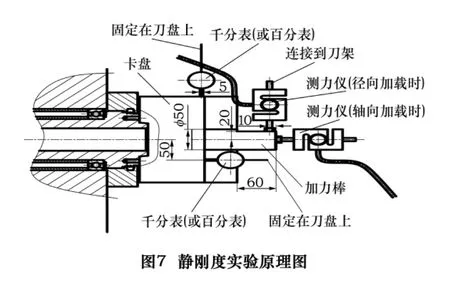
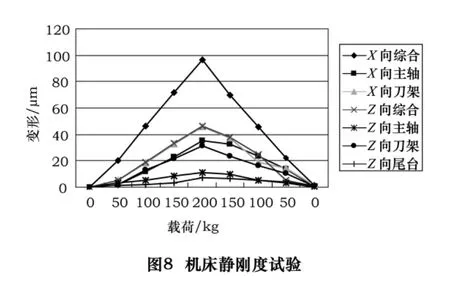
图8是各项静刚度测试结果曲线汇总。在加载过程中，机床的静刚度具有较好的线性度，而在卸载过程中，静刚度表现出一定的非线性，尤其在主轴X向静刚度上表现较为明显。同时在卸载完成后，测试对象的变形量并没有回复到加载前的位置，而是有一定的变形残留，即表现出一定的迟滞性，迟滞量大致在1.5 μm以内。由于加力较小，实体变形都处于弹性变形范围内［12］，分析原因可能是结合面变形未完全回复所致。这与20世纪60年代末基尔萨诺娃等的研究(结合面的切向变形与切向载荷之间成非线性关系)以及Kirsanova、Masuko、益子、Burdekin 等的研究(结合面的切向加载和卸载曲线之间存在迟滞现象，即使在切向载荷小于结合面最大静摩擦力的情况下也如此)是相一致的。

试验数据经过均值处理后就可以利用静刚度计算公式进行计算，计算公式见式(1)。表1是各项静刚度的测试结果和有限元分析结果的对比汇总。

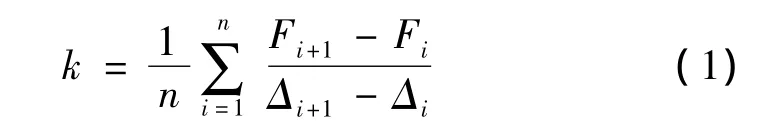
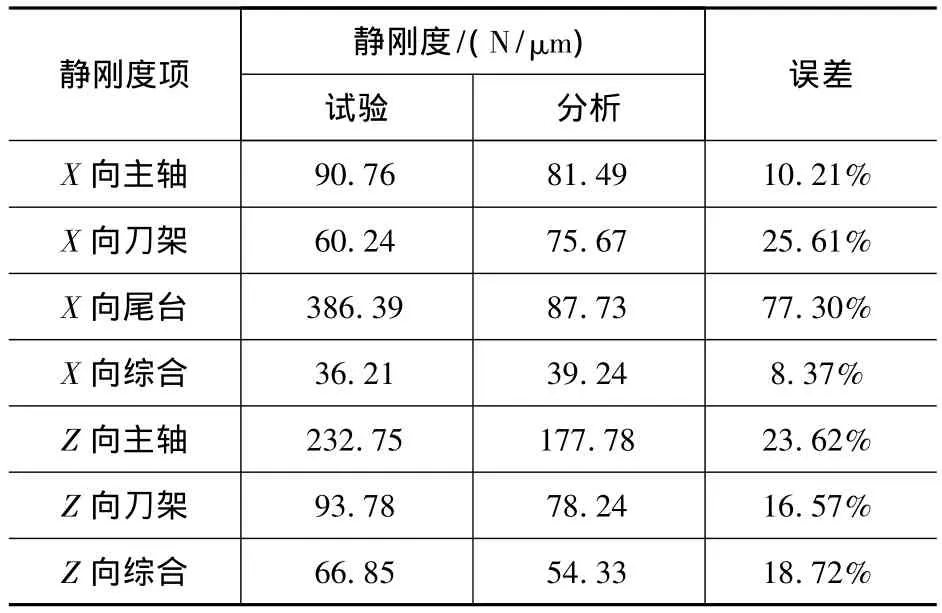
表1 机床静刚度汇总表

从对比结果看，尾台的X向刚度误差较大，可能原因是:尾台实际上有液压卡紧机构，而有限元模型中将这一机构和功能忽略了，导致分析刚度远小于测试结果。从整体来看，有限元分析结果和测试结果具有较好的吻合度，若以测试结果作为真值，则有限元分析结果的误差基本在26%以内。

4 部件有限元分析

从理论上讲，机床上任何承受及传递有效外载荷的零部件及其之间的连接关系都会影响其综合刚度。而且，整台机床各零部件刚度的合理匹配也非常重要。无论对机床进行静刚度分析还是动刚度分析，其最终目的都是通过刚度模型来分析数控机床的工作末端刀具和工件的相对位移，从而分析机床刚度对加工精度的影响。刚度测试和整体有限元分析只能从宏观的角度审视机床的刚度情况，如果想进一步分析刚度的分布情况甚至定位机床刚度的薄弱环节，就必须进行部件级的有限元分析。

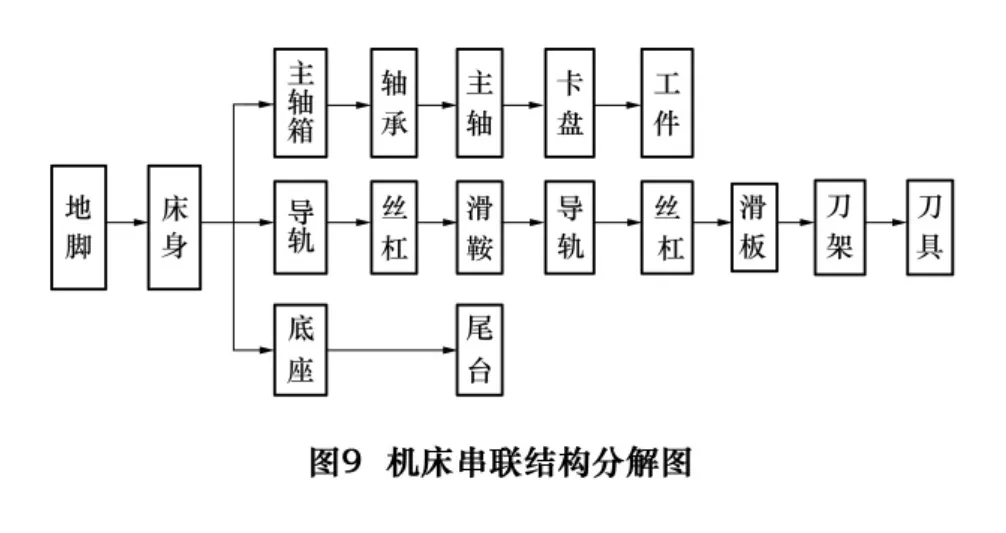
对部件的详细分析采用数控机床串联刚度场理论，从串联刚度场图谱中，可以很容易地分析出各部件位移量占系统总位移量的百分比、系统刚度的拐点等特性，从而描绘出一个完善的机床刚度分布情况、找出系统刚度的薄弱环节［13］。分析机床的整体装配结构大致可以分解为3条串联结构，每一条串联结构都从地脚出发最后到达工作终端，如图9所示。

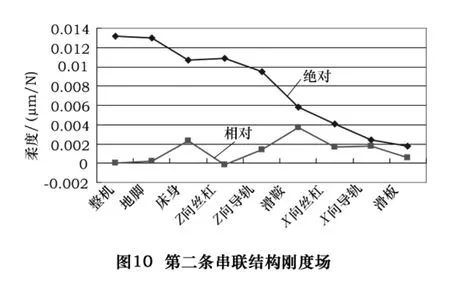
依据测试和分析结果，机床X向综合刚度较低，而X向刀架刚度又是其中最低的，因此仅对第二条串联结构在X向的刚度进行深入分析。图10是根据串联刚度场理论采用有限元分析方法得到的机床X轴方向第二条串联结构的刚度场曲线。图11是串联结构中各个部件(包括结合面等连接关系)对系统总刚度的贡献量柱状图。

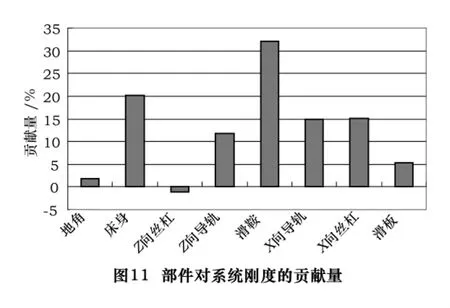
从分析结果看，Z向丝杠对第二条串联结构在X向的刚度贡献量为－1.065 1%，考虑到建模和分析误差等因素的影响以及实际的机床装配关系，可以认为Z向丝杠对第二条串联结构在X向的刚度无影响。图12是去除Z向丝杠后计算得到的机床X轴方向第二条串联结构的刚度场曲线。

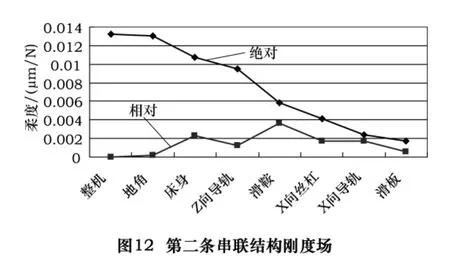
从整个分析结果看，机床在X方向的第二条串联结构的刚度曲线走势较平缓、刚度分布较合理，相对来说滑鞍及其连接对系统的刚度影响最大，占到32%。因此，如果想改善机床的刚度情况可以首先考虑从这一环节入手。

5 结语

机床的静刚度是表征机床性能的最基本的技术指标之一，本文通过将有限元分析技术和实际的测试环节相结合，在保证有限元分析结果准确性的基础上，采用串联刚度场理论进行了详细的结构分析，为了解机床刚度分布和有针对性地进行结构优化提供了必要的基础数据支持。

［1］ASME B5.57 － 1998，Methods for performance evaluation of computer controlled lathes and turning centers［S］.

［2］FU WP，HUANG YM，ZHANG GP.Experimental investigation on damping behavior of normal joint surfaces at unit area［J］.Modeling，Measurement and Control，1993，B51(5):13 －20.

［3］王世军，黄玉美.机床导轨结合部的有限元模型［J］.中国机械工程，2004，15(18):1634 －1636.

［4］ABELE E，ALTINTAS Y，BRECHER C.Machine tool spindle units［J］.Annals of CIRP，2010，59:781 －802.

［5］JIANG Shuyun，MAO Hebing.Investigation of variable optimum preload for a machine tool spindle［J］.International Journal of Machine Tools and Manufacture，2010，50:19 －28.

［6］史安娜，刘春时.数控机床主轴部件变形的有限元分析［J］.组合机床与自动化加工技术，2005(4):26－27.

［7］何晶昌.机床主轴组件刚度ANSYS分析［J］.中国制造业信息化，2006，35(11):32 －33.

［8］赵宏林，张文河，盛伯浩，等.机床整机综合特性的预测［J］.制造技术与机床，1998(3):12 －14.

［9］王世军，黄玉美.机床整机特性的有限元分析方法［J］.机床与液压，2005(3):20－22.

［10］郭显平.机床固定结合部动力学建模及影响因素研究［D］.武汉:华中科技大学，2008.

［11］戴曙.机床滚动轴承应用手册［M］.北京:机械工业出版社，1993.

［12］YANG Guitong.Theory of elasticity and plasticity［M］.北京:中国工业出版社，2005.

［13］刘启伟，张耀满，林剑峰，等.数控机床串联刚度场及其应用研究［J］.制造技术与机床，2011(2):29 －32.