数控机床双边驱动不同步对加工精度的影响*

李初晔 王海涛 邓 凌

(北京航空制造工程研究所数控制造技术航空科技重点实验室，北京 100024)

数控机床作为大飞机制造中的关键设备，设计水平的高低直接影响飞机零件的性能。目前在航空厂应用广泛的高架桥式高速数控机床是从龙门型机床发展出来的，高架桥式高速数控机床为了有效减少移动部件的质量，将立柱从龙门中分离出来，立柱与床身或地基固定在一起，仅使横梁在立柱上进行运动。该类机床的显著特点是:横梁高架在混凝土立柱上，宽度很大，目的是要得到大的坐标行程，满足加工大型航空零件的需求。这类机床工作力较小，对加工精度的影响主要是在自重力下随着坐标的移动而使横梁滑枕结构的弯曲和侧倾变形量不断发生变化，造成刀具点的位置偏离理论加工位置，引起加工误差。另一方面，由于横梁宽度较大，双边驱动如果发生不同步现象对加工点造成较大的误差，因此机床设计要保证双边不同步量在允许范围之内。在机床的调试过程中，双边同步调试花费的时间最多，一直以来是影响机床产出进度和性能的主要问题。因此，对双边驱动不同步现象的研究具有重要意义。

本文的研究内容来源于航空基金课题及重大装备专项，针对航空高档数控机床在加工制造过程中的精度不稳定现象进行研究，推导建立了运动直线度与驱动不同步量之间的关系，为机床设计和机床控制提供理论依据。

1 单边驱动的偏差极限

不同步偏差的允许极限值是由机床本身特性决定的，除控制系统因素外，与导轨长度、导轨间距、横梁与滑动导轨间隙有关。图1中由于间隙的原因，单边运动驱动方式可能产生左右沿运动方向的最大位置偏差δ。图中a为运动件与导轨的接触长度，b为运动件的宽度，c为单边间隙，α为运动件由于间隙产生的最大偏角，δ为两边前后方向不同步位置偏差。

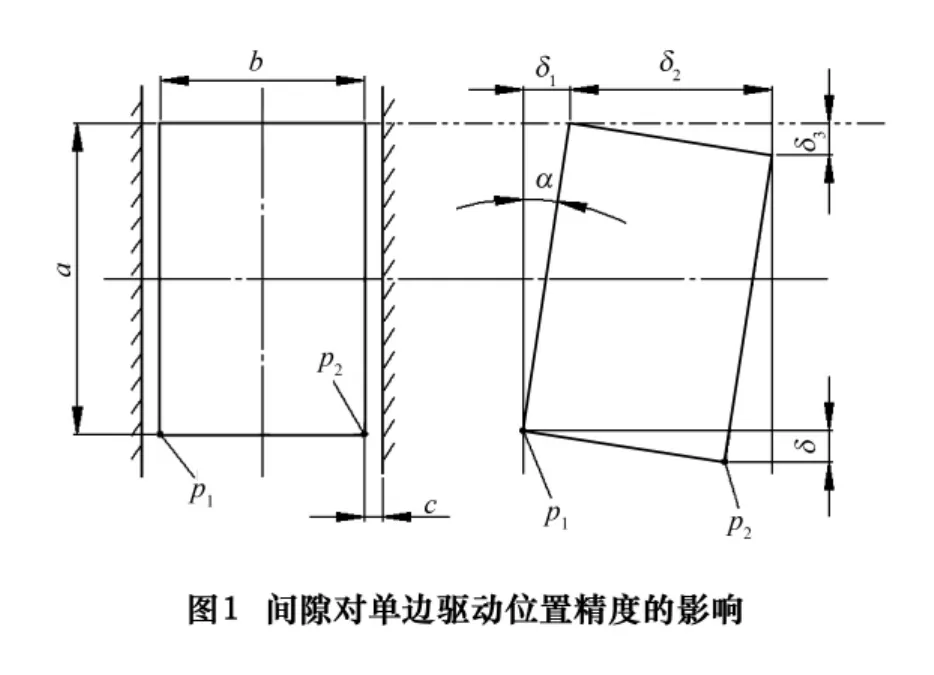
分析图1，小间隙情况下由于α很小有以下关系存在:

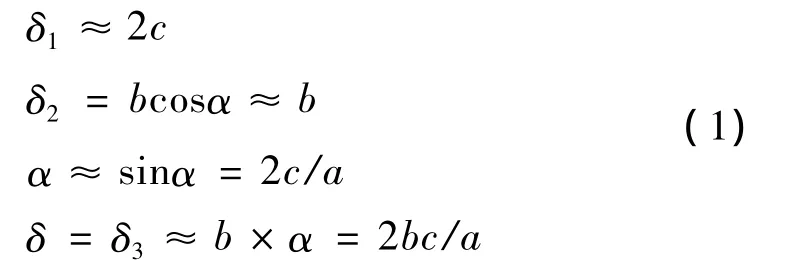
δ为可能达到的最大左右位置偏差，若运动驱动源中心与运动件质心的连线与运动方向完全重合，则驱动不会产生偏角α，左右位置偏差δ为0。一般情况下驱动产生的左右位置偏差为δ，驱动力作用线到质心的距离e称为驱动力偏心距。由于驱动力远远没有对运动件产生弹性变形的能力，因此分析过程中将运动件作为刚体处理，运动件与导轨间的间隙是对运行精度影响的主要原因。

2 单边驱动的运动状态分析

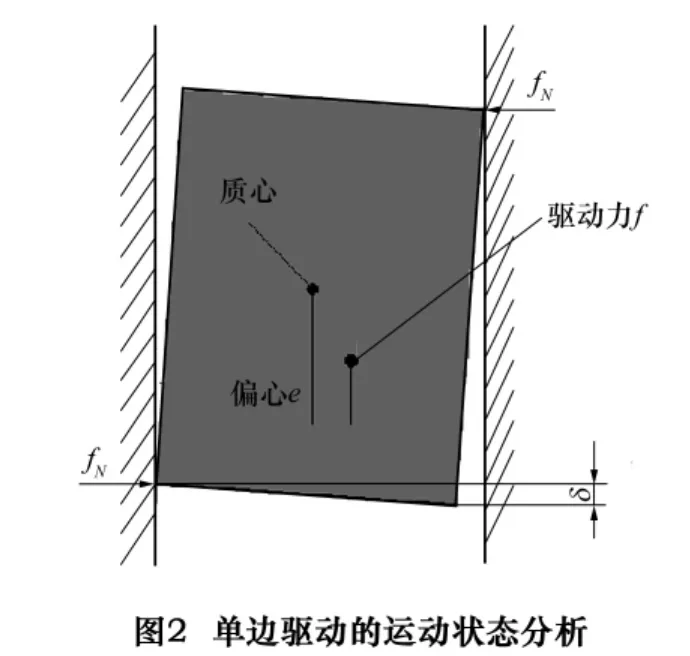
分析表明机床驱动卡死状态与运动件的结构形式有关，与驱动力大小无关。图2中，设运动件的重量W，质量m，驱动力f，驱动力偏心距e，摩擦系数 μs，运动件的位移s、速度˙s、加速度¨s。由力矩瞬时平衡可知，作用于导轨上的正压力fN满足关系式:

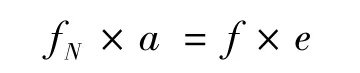
作用于运动体上的合力fq为:

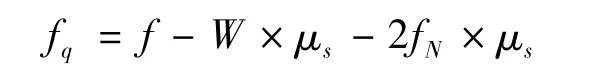
运动件要发生运动，必有fq＞0，得到:

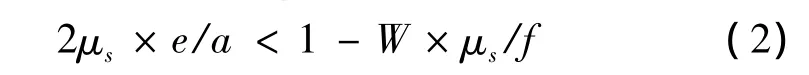
由式(2)知，当e=0时:

式(3)是运动体保持运动状态的驱动力与摩擦力之间的关系，即保持运动状态至少克服底面摩擦力。因为主要考察侧导轨摩擦力对运动状态的影响，为表达方便忽略底面摩擦，式(2)变为:

给定摩擦系数μs和运动体长度a，由式(4)可得到一偏心距e，称为对应于a、μs的极限偏心距。要使物体运动，驱动力偏心距必须小于极限偏心距;反之，无论驱动力多大，物体始终处于卡死状态。

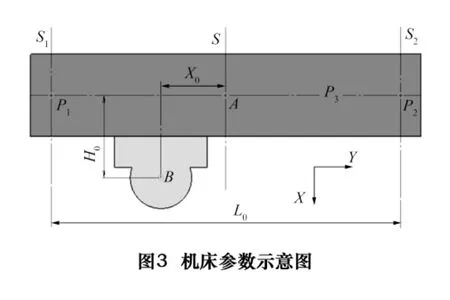
3 双边驱动不同步计算

图3中，S1、S2为左右导轨的中心线，S为横梁沿X方向的中心线，S3为过横梁重心的水平线，P1、P2为S1、S2与S3的交点，A为横梁重心，B为铣刀中心点。横梁左右导轨间距离L0，B到S3的距离H0，铣刀中心点离横梁中心的距离即B到S的距离为X0。

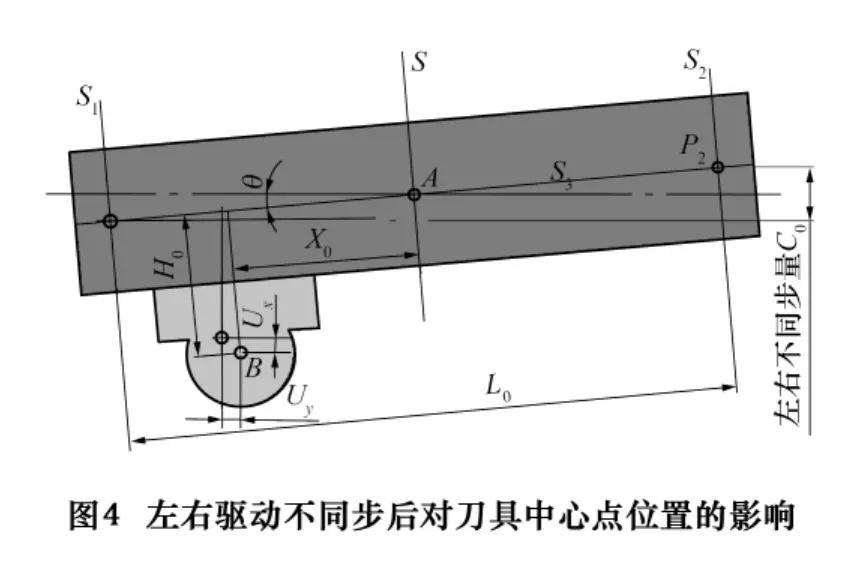
假设左右不同步量为C0，由于左右不同步，P1、P2点沿X方向有C0的位置偏差，使横梁绕Z轴发生偏转(图4)，偏转角度θ为:

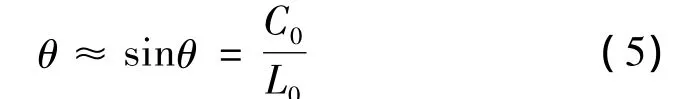
当P1超前P2点时，刀具中心点B沿X方向的位置偏差为:

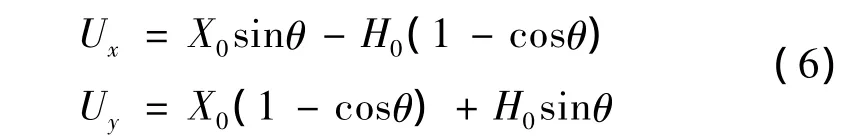
将上式展开为幂级数形式:

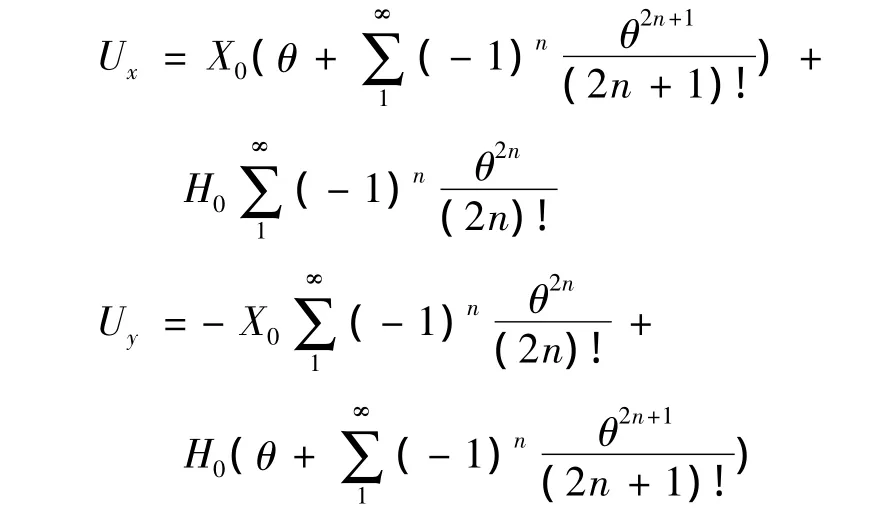
因为横梁的偏转角度θ很小，忽略θ的2阶以上高阶量，Ux、Uy近似为:

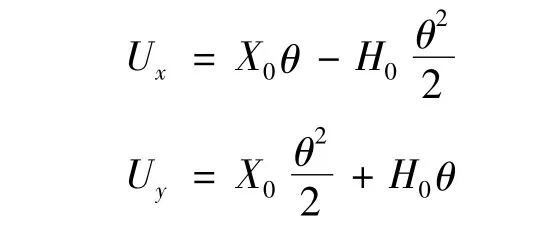
将θ的表达式代入上式，得到刀具中心点的位置偏差与左右不同步量之间的关系:

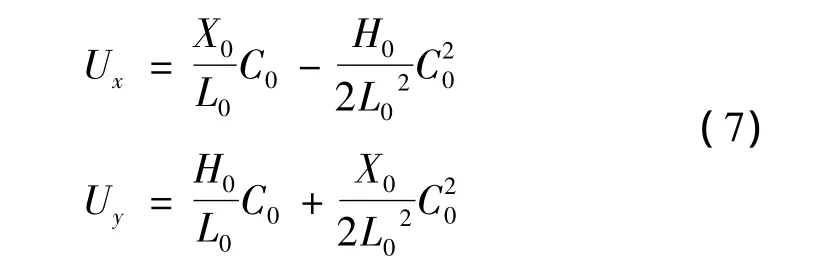
当P1落后P2点时，刀具中心点B沿X方向的位置偏差为:

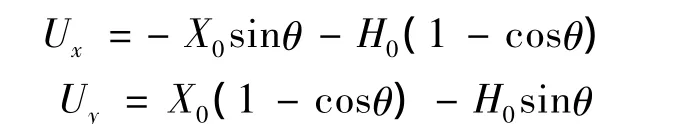
得到刀具中心点的位置偏差与左右不同步量之间的关系:

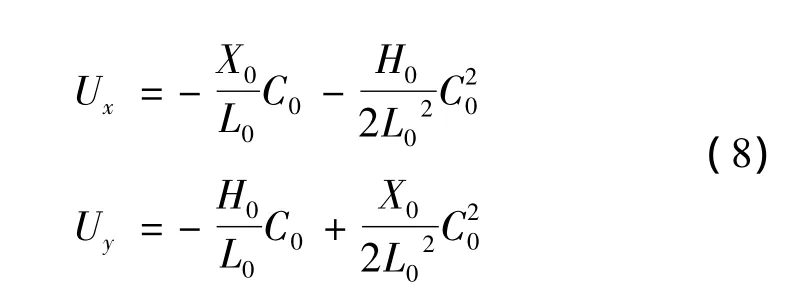
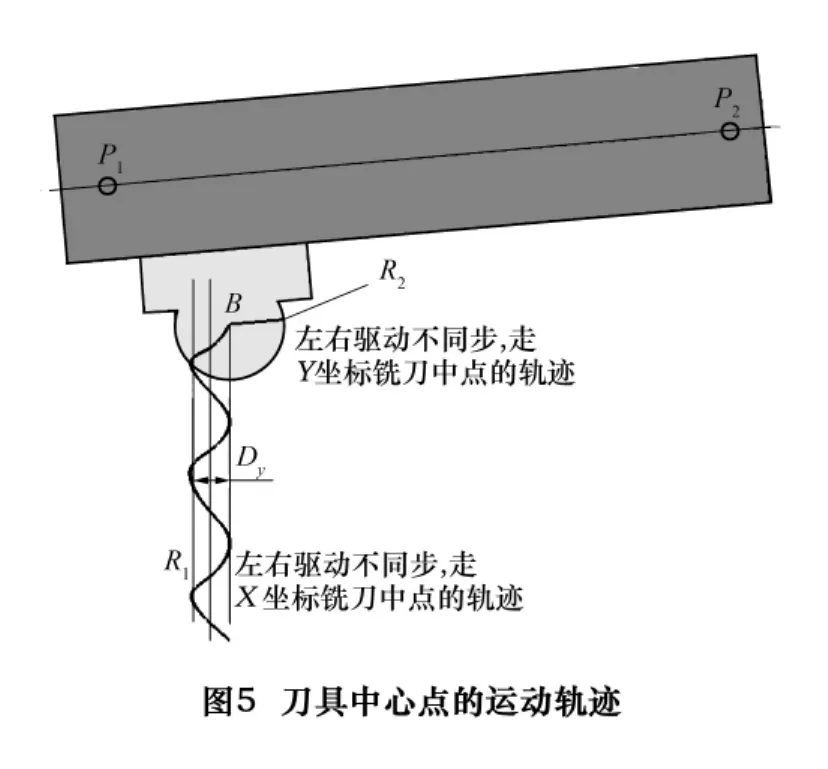
当横梁走X坐标，左右不同步使P1、P2交替超前，横梁绕Z轴往复摆动，刀具中心点B走出图5中的R1曲线;当X位置保持不动，滑板走Y坐标时，刀具中心点B走出图中的R2曲线。图中Dy的值等于式(7)、(8)Uy值的代数差:

Dy反映了不同步量对X移动直线性的影响，当X位置不变，只走Y坐标时刀具中心点走出的是直线，因此在X向固定的情况下左右不同步对Y坐标移动直线性没有影响。当X、Y坐标同时移动时，不同步走出图6中的曲线，曲线变化的频率与P1、P2点前后摆动频率有关。

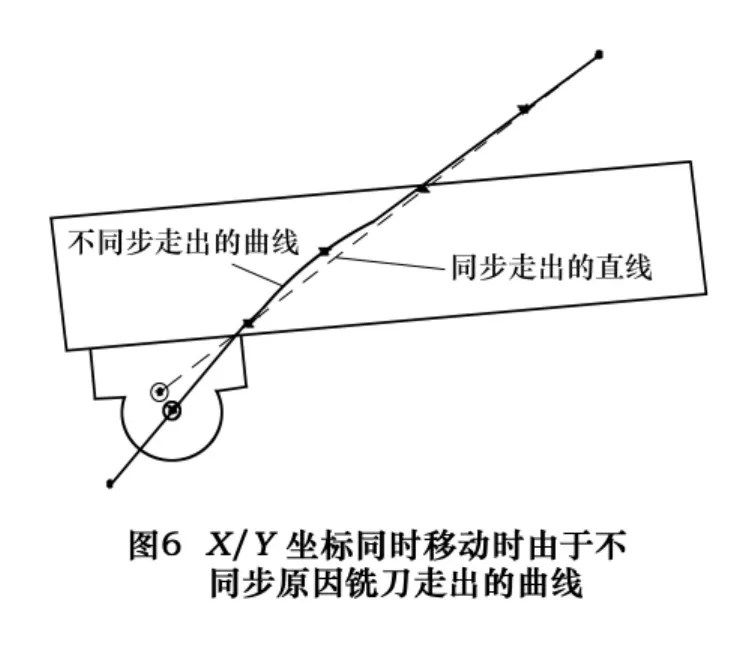
公式(9)是X向运动直线度与双边驱动不同步量的关系式，当不同步量已知时，可导出横梁X向运动直线度偏差。反之，当X向移动直线性的控制精度Dy为已知量时，可以由式(9)变换计算出左右不同步允许量的数值:

工程中应尽量减小机床的运动直线度偏差，从式(9)看出，当C0已知时，通过增大L0/H0比值使直线度偏差Dy变小，因此在横梁导轨间距离L0已定的条件下，机床设计时应尽量减小H0值。反之当控制精度Dy已定时，比值L0/H0越大，不同步允许值C0越大，更利于控制程序的实施。比值L0/H0就像一个放大器，在运动直线度和不同步允许量之间建立了联系。

为成飞提供的三坐标机床的参数为:L0=5 200 mm，H0=680 mm，X向行程9 000 mm，Y向行程3 000 mm。将参数代入式(9)，得到三坐标机床不同步量为C0时对X向移动直线性影响量为:

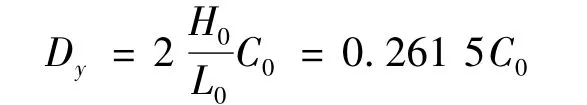
当X向移动直线性的控制精度Dy为已知量时，由式(10)该三坐标机床不同步量的允许值为:

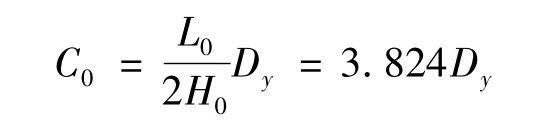
机床X向直线度要求Dy=0.03 mm，则C0的理论设计值不能超过0.115 mm，C0值可为控制程序设定提供理论依据。

4 结语

本文首先从数控机床单边驱动入手，研究了由间隙引起的单边驱动的运动偏差，并对造成机床运动卡死的原因进行了原理分析，计算了单边驱动的极限偏心矩，最后对双边驱动不同步量对刀具中心点位置精度的影响规律进行研究，导出了两者之间的关系方程，为提高机床精度，加快机床的调试进度提供重要的理论保证。

［1］张萌，李航，杨丙乾.数控机床运动精度及其研究［J］.机械设计与制造，2008(12):106－108.

［2］刘又午，赵小松，刘丽冰.基于多体系统理论的数控机床误差分析辨识与补偿［J］.中国机械工程，1998，9(3):88 －98.

［3］谢书法.提高柔性加工机床的加工精度的方法研究［J］.电子机械工程，2007(6):47－52.

［4］洪迈生.精度诊断在先进制造技术领域中的重要作用［J］.振动测试与诊断，1997(4):1－11.

［5］林其骏.机床数控系统工程［M］.北京:中国科技出版社，1991.

［6］周骥平.机械制造及自动化［M］.北京:机械工业出版社，2001.