上海证劵市场股票网络的复杂网络特性研究

刘晓霞，王卫华

（武汉理工大学理学院，湖北 武汉 430070）

自然界中大量的复杂系统可以用网络来抽象和描述［1］。为了通过对复杂网络的研究抽象出大量复杂系统所具有的共同特性，科学家们引入了很多概念和理论，其中最基本的3个概念为网络的特征路径长度、聚类系数和网络的度分布。并以此3个概念为度量标准研究发现，大量的复杂网络具有小世界特性［2－4］。此外，随着人们对复杂网络进行深入广泛的研究，发现 Internet网［5］、广义合作网［6］等在具有小世界特性的同时还具有无标度特性，即节点度分布可以用幂率形式大致描述。

证券市场作为一个复杂的经济系统，可以用复杂网络来抽象和描述。复杂网络理论是研究股票市场内在结构和功能的有力工具，股票关联网络的拓扑性质和聚类结构对于理解网络的形成机制、发生在网络上的动力学行为具有重要意义。黄玮强等研究了中国股票网络的拓扑性质并对聚类结构进行了分析［7］。

由于现实世界的很多系统可以用复杂网络来描述，证券市场作为经济系统也不例外，可将网络的节点作为证券市场的股票，网络的连边为股票价格波动的相关性。此外运用复杂网络的理论来研究该网络的拓扑性质，经过实证研究发现该网络与现实世界的大量复杂网络一样具有小世界特性和无标度特性。

1 上海证券市场股票网络的构建方法

网络的节点集合为在上海证券市场上市的股票，对于取定的阈值θ，如果两个节点i和j的价格波动相关系数cij＞θ，则使两个节点之间连边，否则不连边。并且构造的网络为无向网络，即若节点i与j之间有边相连则节点j与i之间也有边相连，并且不考虑连边的权重大小，将其均视为1。故最终将股票网络初始化为无向无权的网络。

假定xi（t）为公司t时刻的股票收盘价格，则股票的对数收益率定义为:

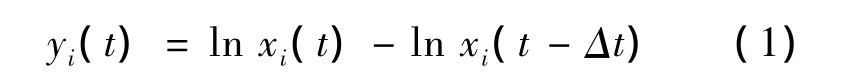
其中，Δt为1 天，i=1，2，…，N。为避免外部经济环境如利率、汇率和通货膨胀等对股价收益率互相关系数的影响，做如下处理:

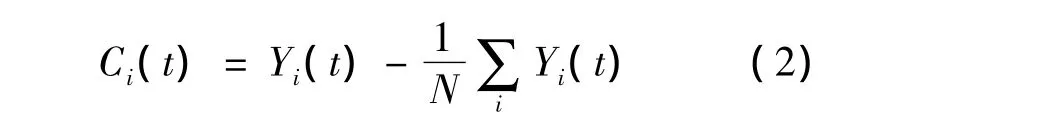
其中，Ci（t）为在t时刻股票i对所有N个公司股票收益率均值的相对收益，进一步，可以计算出股票收益率的互相关系数为:

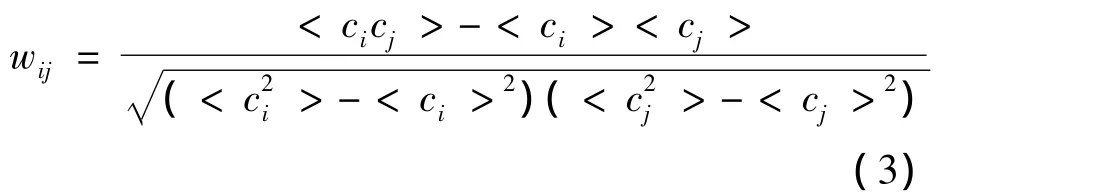
其中，＜·＞表示取时间平均，wij为股票i与股票j之间的连接权重。

笔者选用的数据节点为2000—2011年在上海证券交易所持续上市的股票，共884个，用股票的周收盘价格来计算对数收益率。数据的处理方式为以每一只股票的周收盘价格在2000年初的价格为基点进行后项除权，共收集了180个股票收盘价格（选用的数据来自雅虎财经）。

经Matlab仿真研究，根据上述数据得到相关系数概率分布图如图1所示。

图1 上海证券市场股票相关系数概率分布

2 复杂网络中的基本概念

2.1 平均路径长度（特征路径长度）

在复杂网络中，连接两个节点的最短路径（即经过的边数最少）的边的数目称为两个节点i与j之间的距离dij。最短路径定义为所有连通（i，j）的通路中，所经过其他顶点最少的一条（或几条）路径。网络的平均路径长度 L为网络中任意一对顶点的最短路径长度的平均值，即:

其中，N为网络的节点个数。它描述了网络中分离任意两个顶点所需的平均步数。网络的平均路径长度也称为网络的特征路径长度。

2.2 聚类系数

在人际关系网络中，某一个人的两个朋友很可能彼此也是朋友，将人际关系网络的这种特性描述为聚类性［8］。一般地，假设网络中的某一个节点i有ki条边与它相连，则对应相连的这ki个节点均称为它的邻居节点。显然，在这ki个节点之间最多只可能有ki（ki－1）/2条边，而这ki个节点之间实际存在的边数Ei与总的可能的边数ki（ki－1）/2的比值定义为节点i的聚类系数Ci，即:

同理，整个网络的聚集系数C定义为所有节点的聚集系数Ci的平均值。

2.3 度和度分布

节点i的度用ki表示，定义为与节点i相连的其他节点的个数。一个节点的度值越大意味着与它相连的边的数目越多，它在网络中越重要。如果该节点受到攻击，网络更容易陷入瘫痪状态。

在一个无向的网络中，网络的平均度被定义为所有节点的度取平均值，用＜k＞表示。网络中节点的度分布函数用p（k）来表示，它被定义为从网络中任意取一个节点其度值恰好为k的概率。

3 证券市场构造的股票网络特性

3.1 小世界特性

平均路径长度L的定义如上所述。在不同的网络中，平均路径长度有其不同的含义，例如在文献［4］的小世界实验中，平均路径长度表示可以最少通过几个人将网络中的所有人相连接，通过研究发现，地球上任意两个人的平均距离为6，这就是著名的六度分离理论（six degrees of separation）。如果一个复杂网络的规模很大，节点数目很多，但网络的平均路径长度却很小，就称该网络具有小世界效应，用定性的语言可以描述为:对一定的节点平均度＜k＞，网络的平均路径长度L的增长速度至多与网络节点数N的对数成正比。

刻画小世界特性的另一个度量指标是聚类系数，聚集系数C用来描述网络中节点的聚集情况，即网络有多紧密。若研究网络具有较小的特征路径长度和较大的聚类系数，则认为该网络为小世界网络。这里的较小、较大比较均以随机网络为参照对象。

Lrandom为随机网络的特征路径长度当量；Crandom为随机网络的聚类系数。若随机网络与所研究的网络具有相同数目的节点和边。一般可以表示为:

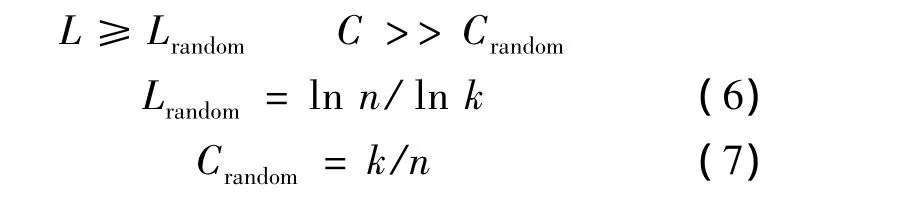
式中:k为网络的平均度，取2Q/n（Q为网络的边数）。

由于所关心的是股票之间的强影响，而对于那些联系不是很紧密的股票可以忽略它们之间的关联，故在根据以上数据得到的邻接矩阵中取阈值为较大的值，忽略网络中关联较小的一些节点，得到的对应阈值、平均路径长度和群聚类系数如表1所示，平均最短路径的计算采用图论中的dikstra 算法［9］。

表1 不同阈值下股票网络的拓扑特征

对应具有相同数目节点和边的随机网络的平均路径长度Lrandom，群聚类系数Crandom的对应数值如表2所示。

表2 与股票网络具有相同数目节点和边的随机网络的拓扑特征

由于股票网络的平均路径长度与同等规模的随机网络相当，而聚类系数又比同等规模的大得多，从表1和表2中的数据可以很明显地发现，股票网络是一个小世界网络，该网络的平均路径长度比较小，其实际意义表明网络中的任意两只股票可以很方便地连接。由于网络的连边表示股票价格波动的相关性，因此在该股票网络中，如果一只股票的价格发生变化，网络中的其余股票很容易受到影响。表1和表2中的数据还表明网络有比较大的聚类系数，说明股票价格的波动在某只股票的邻居集团内更加容易传播，并且影响的程度会更大。

3.2 无标度特性

度分布是描述网络性质的一个重要统计量，定义为随机选择一个节点，度恰好为 k的概率［10］。科学家们通过大量的实证研究发现，很多现实世界中网络的节点度可以近似用幂率分布来描述，即p（k）近似为幂函数。在直角坐标系下，幂函数的图像下降相对缓慢，这就意味着度值很大的节点在网络中也是存在的，称其为网络的Hub节点，在无标度网络中，Hub节点起着至关重要的作用，它们常常左右着网络能否正常运作。无标度网络的度分布函数在双对数坐标系下可以近似用一条直线来拟合。

为验证股票网络的无标度特性，这里设定网络的阈值为0.58，研究上海证券市场股票网络节点的度分布情况。从图2可以看出，经过Matlab仿真在双对数直角坐标系下，其度分布曲线大致在一条直线的附近，直线的斜率为－0.87445，表明该网络在阈值θ=0.58时节点度服从幂率分布，且幂指数为0.87445。因此，上海证券市场网络在阈值θ=0.58时为无标度网络。也就是说上海证券市场股票网络连接遵循择优连接的“马太效应”。一只新上市股票的价格波动更容易受到在网络中具有很多连接的Hub节点的影响。

图2 阈值为0.58时网络的度分布双对数分布曲线

实际网络的幂指数一般在（2，3）之间，股票网络具有比实际网络较小的幂指数，但这也是有其实际意义的，这是因为证券市场股票网络本身就是一个虚拟的网络，网络中节点的连接不会受到现实中技术资源的影响和限制，不需要高昂的构造费用。此外股票网络是一个无标度网络且幂率指数相对较小，表明在给定的阈值下，证券市场股票网络起关键作用的Hub节点较多，在股市上的交易过程中有很大一部分的股票都具有较强的影响力，它们价格的波动会对当日股市整个行情的稳定起着非常大的影响作用。

4 结论

笔者对上海证券市场股票网络从网络拓扑特征上进行了分析，分别计算了其在不同阈值下对应的平均路径长度和聚类系数，并和与其具有相同数目节点和边的随机网络进行比较，得出股票网络具有明显的小世界特性，继而研究了其度分布，发现度分布服从幂率分布，在双对数坐标系下可以近似地用一条直线来拟合，且幂指数为0.87445，说明股票网络同时为无标度网络。

［1］ALBERT R，BARABSI A L.Statistical mechanics of complex networks［J］.Rev Mod Phys，2002，74（1）:47 － 97.

［2］WATTS D J，STROGATZ S H.Collective dynamics of"small world"network［J］.Nature，1998，393（5）:440 －442.

［3］NEWMAN M E J.The structure and function of complex networks［J］.SIAM Review，2003，45（2）:167 －256.

［4］MILGRAM S.The small world problem ［J］.Psychology Today，1967，2（1）:60 － 67.

［5］SIGANOS G，FALOUTSOSOS M，FALOUTSOSOS C，et al.Power laws and the AS level internet topology［J］.IEEE/ACM Transactions on the Networking，2003，11（4）:514 －524.

［6］张培培，何阅，周涛，等.一个描述合作网络顶点度分布的模型［J］.物理学报，2006（55）:60－67.

［7］黄玮强，庄新田，姚爽.中国股票关联网络拓扑性质与聚类结构分析［J］.管理科学，2008，21（3）:94 －103.

［8］闵志锋.中国证券市场的复杂网络特性研究［D］.沈阳:东北大学图书馆，2007.

［9］BUCKLEY F，LEWINTER M.图论简明教程［M］.李慧霸，王凤芹，译.北京:清华大学出版社，2005:32－89.

［10］张娜.复杂网络社区结构划分算法研究［D］.大连:大连理工大学图书馆，2009.