基于等距节点的数值求积公式在Brownian桥测度下的平均误差

刘 洋，许贵桥

基于等距节点的数值求积公式在Brownian桥测度下的平均误差

刘 洋，*许贵桥

（天津师范大学数学学院，天津 300387）

本文讨论了基于等距节点的数值求积公式在Brownian桥测度下的平均误差，得到了相应量的准确值。

-平均误差；数值求积公式；Brownian桥测度

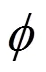
而基于

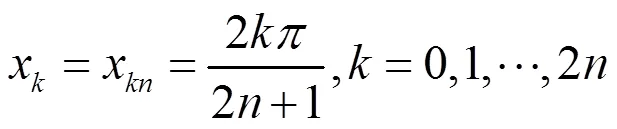
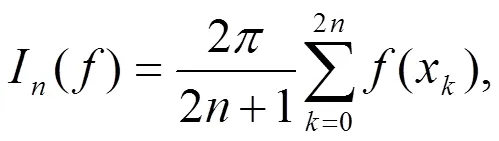
本文得到

1 定理1的证明

由 (1),(2),(3) 可知

由(7)知其方差为

由(8)和(5)可知

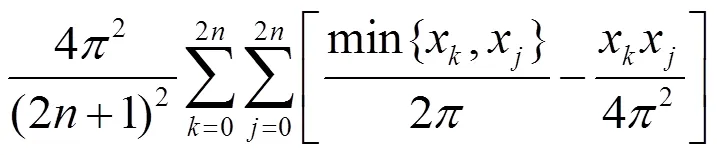
直接计算可得

由(2)经简单计算可得

(12)

因此

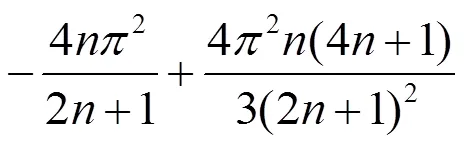
同时

由 (9)，（10），（14）和（15）可得

由(6)，(16) 及 (18) 可得定理1的结论。

[1] Traub J F, Wasilkowski G W, Wozniakowski H. Information-Based Complexity[M]. New York: Academic Press, 1988.

[2] Klaus R. Average-case analysis of numerical problems[M].Berlin-Heidelberg-New York: Springer- Verlag, 2000.

[3] 许贵桥, 杜英芳.三角多项式算子在 Brownian 桥空间下的平均误差[J].数学学报, 2009, 52(3): 523-534.

[4] Lifshits M A. Gaussian Random Functions[M]. Kluwer: Dordrecht, 1995.

[5] 李贤平.概率论基础[M].北京:高等教育出版社, 2002.

The Average Error of the Numerical Quadrature Formula Based on the Equidistant Nodes on Brownian Bridge Measure

LIU Yang，*XU Gui-qiao

（Department of Mathematics, Tianjin Normal University, Tianjin 300387, China）

We discuss the average error of the numerical quadrature formula based on the equidistant nodes on Brownian bridge measure. We obtain its corresponding values.

p-average error; numerical quadrature formula; Brownian bridge measure

O174.41

A

10.3969/j.issn.1674-8085.2012.02.003

1674-8085(2012)02-0011-03

2011-12-20；

2012-02-06

刘 洋(1989-)，女，天津人，硕士生，主要从事计算数学研究(E-mail: 347607330@qq.ocm);

*许贵桥(1963-)，男，河北石家庄人，教授，博士，主要从事函数逼近论研究(E-mail: xuguiqiao@gyou.com).