参数选择对模糊控制器动态性能的影响

孔翠香，廖 萍

参数选择对模糊控制器动态性能的影响

*孔翠香，廖 萍

(井冈山大学电子与信息工程学院, 江西，吉安 343009)

模糊控制器的动态性能是设计模糊控制器的一个重要指标，在模糊控制器设计中, 合理地选择模糊控制器的参数非常重要。本文建立了系统仿真模型, 通过Matlab仿真并分析各种控制参数对模糊控制器的控制性能的影响，仿真结果表明只有选择一组最优化的参数, 模糊控制器才会发挥出最佳的性能。

模糊控制器；参数；动态性能；仿真

在自动控制领域中，对于难以建立数学模型、非线性和大滞后[1]的控制对象，模糊控制技术具有很好的控制特性，且所需设备简单，系统鲁棒性[2]强，经济效益显著，它日益受到人们的重视并成功地应用在多个领域。模糊控制器的动态性能是设计模糊控制器的一个重要指标,包括系统的上升特性、超调量、调节时间和稳态误差等。影响模糊控制器动态性能的因素有多方面,如模糊规则，论域的大小，隶属度函数及被控对象结构，量化因子及比例因子等。

文献[3]研究比例因子对模糊控制器动态性能的影响，文献[4]和文献[5]探讨量化因子和比例因子在模糊控制器中的作用及其在线修正。文献[6]研究隶属函数对模糊控制性能的作用与影响.文献[7]提出了基于模糊控制的自适应隶属函数水印潜入方法，本方法模糊规则不够合理。文献[8]采取似末位淘汰的模糊控制规则选择图像水印。文献[9]研究基于模糊规则的队列接入控制方法，以上研究均基于某一个参数研究，本文综合考虑多个参数对模糊控制器的影响，要根据系统的实际要求，在线优化、调整参数，选择一组最优化的参数，从而获得最佳的控制效果。

1 模糊控制器的设计

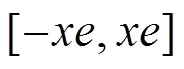
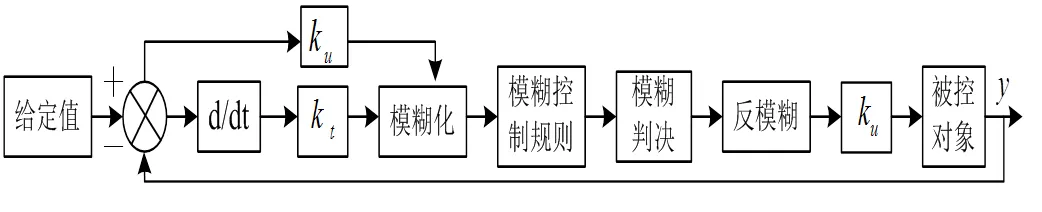
图1 　模糊控制系统原理框图

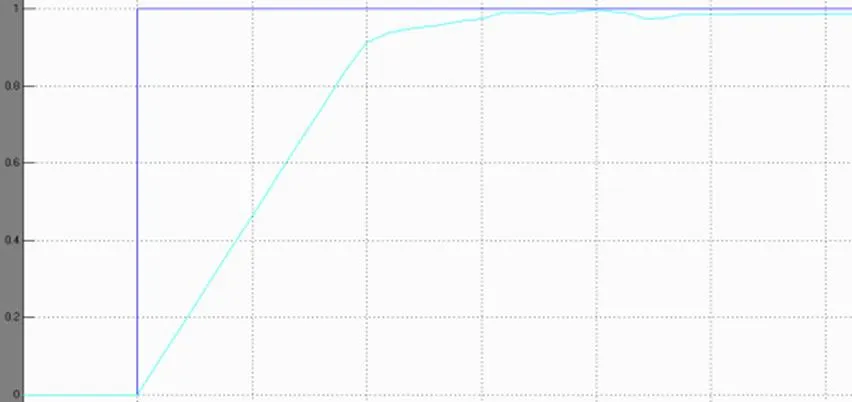
图2 系统动态性能较好时候的阶跃响应

2 参数对系统动态性能影响的仿真分析

2.1 隶属度函数对系统动态性能的影响

不同的隶属度函数形状将对控制特性产生不同的影响,以比较常用的正态分布曲线为例。正态函数为：

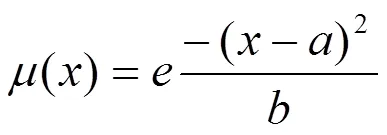
为了研究隶属度函数对系统性能的影响，选取两个均为双输入单输出的模糊控制器，模糊控制器1的误差的基本论域为E=[-1 1]、误差变化率的基本论域为EC=[-0.1 0.1]和输出控制量的基本论域为UC=[-1 1]，模糊控制器1的误差和误差变化率的隶属度曲线为正态分布如图4所示，输出的隶属度为三角型分布如图5所示；模糊控制器2的基本论域与模糊控制器1相同，两个模糊控制器使用同样的规则，其它的比列因子和量化因子也调节相同并且性能达到最佳，控制器2的误差和输出的隶属度也和模糊控制器1保持相同，只改变模糊控制器2的误差变化的隶属度函数曲线的形状，如图2.4所示：

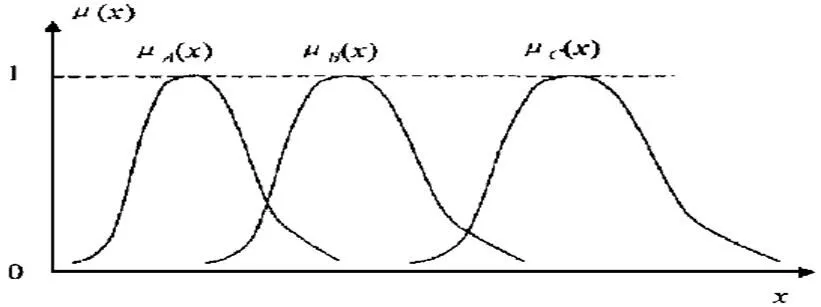
图3 不同分辨率的隶属度函数

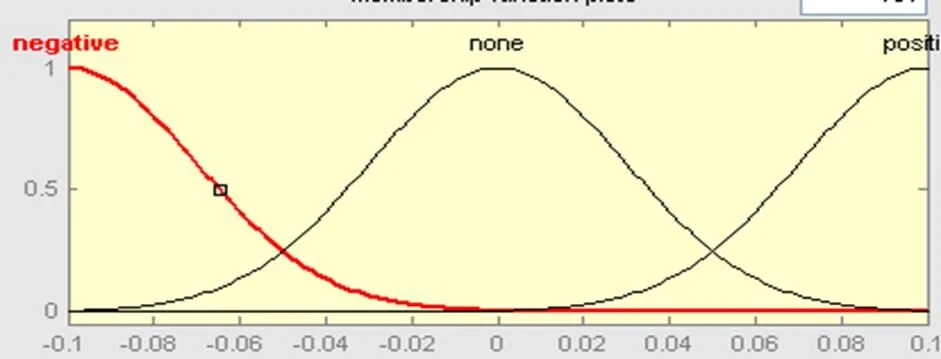
图4 模糊控制器1误差和误差变化的隶属度函数曲线

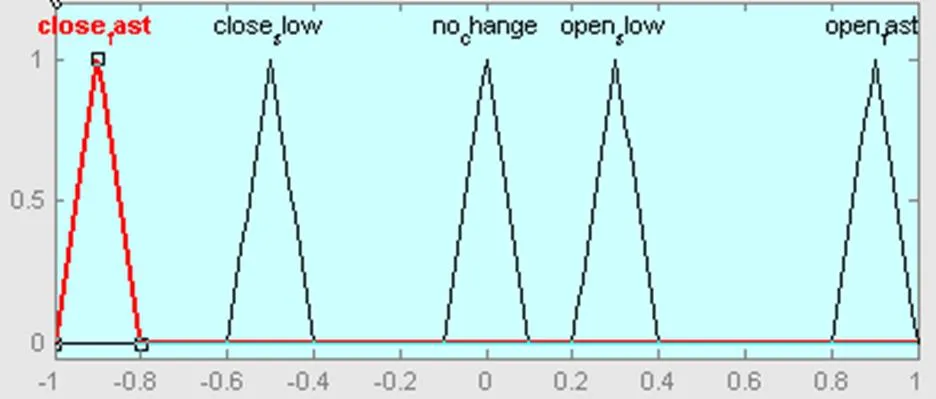
图5 模糊控制器1输出控制量的隶属度函数曲线

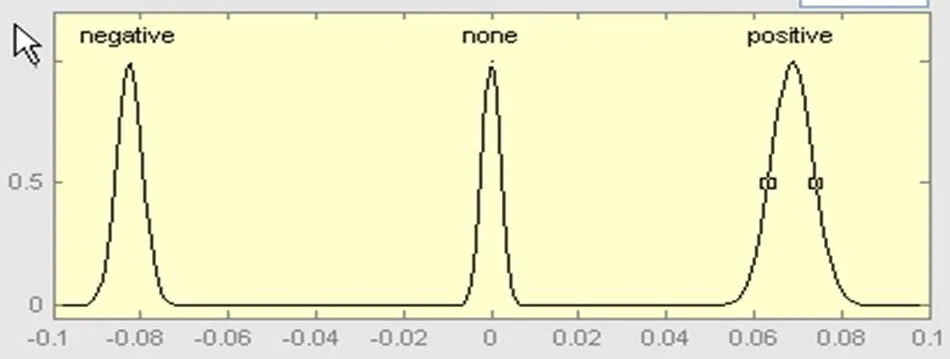
图6 模糊控制器2误差变化的隶属度函数曲线

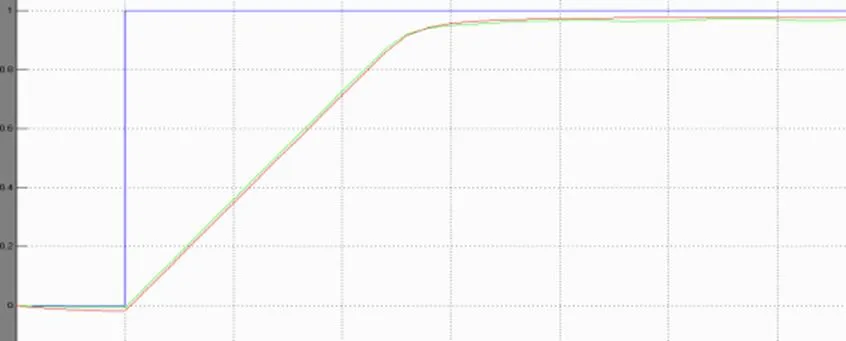
图7 改变其中一个隶属度函数形状后的控制结果

图7中红线为模糊控制器2的结果，绿线为控制器1的结果，可以看出，模糊控制器2的效果更好，分辨率更高，因为2中误差变量的隶属度函数形状更陡，所以分辨率更高，控制灵敏度也就越高。而控制器1中隶属函数的变化较缓慢则控制特性也就越平缓，但系统的稳定性就较好鲁棒性较强。因此,在选择模糊变量的隶属函数时，在误差较小的区域，采用分辨率高的隶属函数，使系统具有较好的灵敏度；在误差较大的论域，采用分辨率低的隶属函数,使系统具有良好的鲁棒性。

同样除了改变模糊控制器2误差的隶属度函数形状外，也可以改变控制器2其他变量的隶属度；或者将某个输入变量的隶属度函数由正态分布改为三角型或梯形等研究对性能的影响；同样也可以改变隶属度函数的间隙,在函数形状相同的前提下，无间隙时控制性能比有间隙时性能更好。

2.2 论域的大小对系统动态性能的影响

众所周知，任何物理系统的信号总是有界的。在模糊控制器中这个有界限一般成为该变量的基本论域，它是实际系统的变化范围。以双输入单输出系统为例，设误差的基本论域为[-xe,xe], 误差变化的基本论域为[-xec,xec], 被控对象实际要求的变化范围的基本论域设为[-yu,yu]。输入变量的基本论域可以通过实验或理论指导来确定，它在控制过程中往往是不变的。设误差的模糊论域为

E={-n1,-(n1-1),…,0,1, …,(n1-1),n1}

误差变化的论域为

EC={-n2,-(n2-1),…,0,1, …,(n2-1),n2}

控制量所取的论域为

U={-m,-(m-1),…,0,1, …,(m-1),m}

一般来说，论域的等级划分越细，控制精度就越高。但过细的划分量化等级将使办法复杂化。

(1)为了研究论域大小对系统性能的影响，选取两个均为双输入单输出的模糊控制器，两个模糊控制器的其它参数完全相同，设两个模糊控制器误差变化率的基本论域为EC=[-0.1,0.1]以及输出控制量的基本论域为UC=[-2,2]，模糊控制器1的误差的基本论域为E=[-1,1]，改变模糊控制器2输入误差论域为E=[-3 ,3]，研究其对系统动态性能的影响。

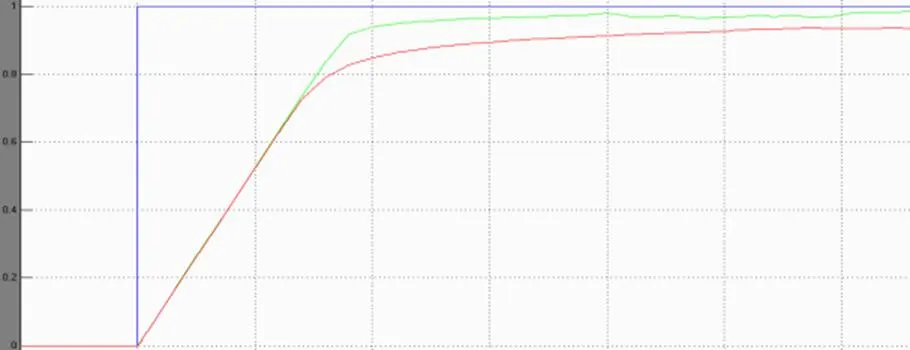
图8 改变模糊控制输入误差E的论域的控制结果

(2)同样，使两个模糊控制器的误差的基本论域E=[-1,1]及被控对象的变化论域UC=[-2,2]，模糊控制器1的误差变化的基本论域为EC=[-0.1,0.1]]，改变使模糊控制器2的误差变化的论域为EC=[-0.5,0.5]，研究其对系统动态性能的影响。

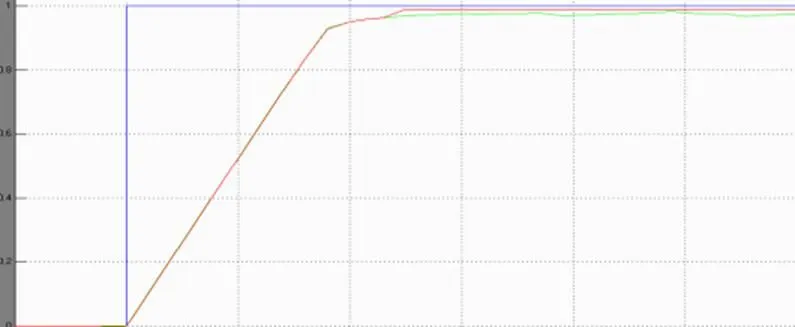
图9 改变模糊控制输入误差变化EC的论域的控制结果

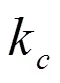
(3)同样，使两个模糊控制器的误差和误差变化的论域都保持不变，使模糊控制器2的控制量的论域UC=[-0.5 0.5]，研究其对系统动态性能的影响。

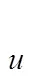
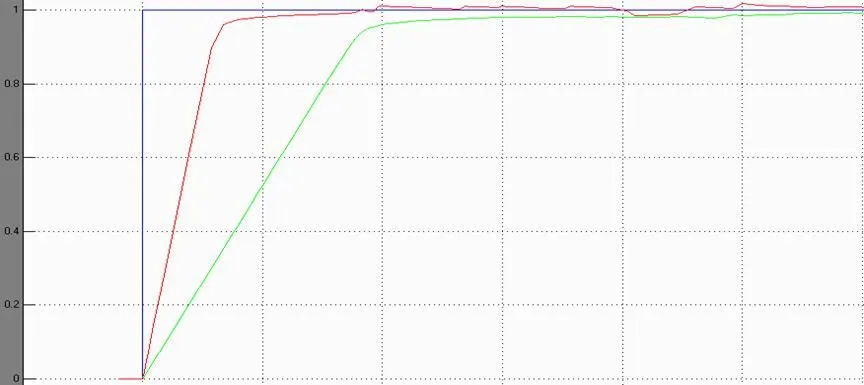
图10 改变模糊控制输入误差变化U的论域的控制结果

2.3 量化因子及比例因子对系统动态性能的影响

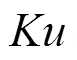
（1）在Kc=20, Ku=0.35 情况下，Ke分别等于7和10时系统响应仿真图

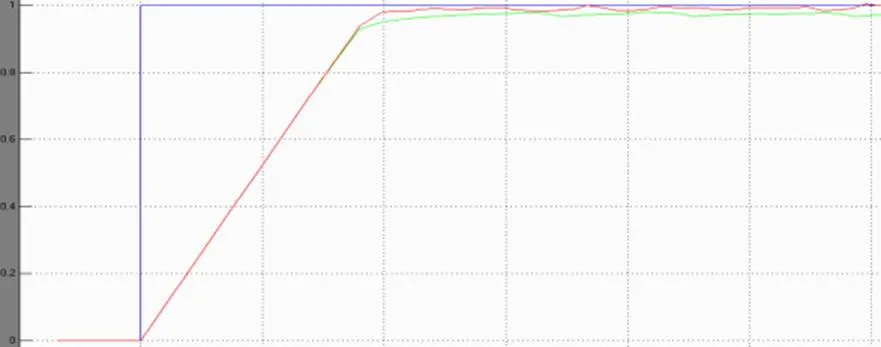
图11 Ke对控制器性能的影响

图11中红色线为Ke较大时的仿真结果，可以看出Ke选得较大时，调节死区越小，系统上升速率较快，系统响应的时间较短,但Ke取的过大，系统的超调量也较大,过渡过程也较长,甚至产生振荡, 使系统不能稳定工作。Ke选择越小，系统超调越小, 但Ke过小，使系统上升速率较小，系统调节隋性变大，也影响系统的稳态性能，使稳态精度降低。

(2)当Ke=7，Ku=0.35时不同Kc的系统响应图

图12 Kc 对控制器性能的影响

图12中红色线为Ke较大时的仿真曲线，可以看出kc选择的越大，但系统的响应速度变慢，系统的超调量越小；Kc较小，系统反应快，超调量大；而Ke过小，将引起调节时间过长，严重时系统不能稳定工作。对系统稳定性的影响在模糊控制系统中，一般不可能消除稳态误差，更不可能消除误差变化率。一般而言，Ke增加，稳态误差将减小；Kc增大，稳态时误差变化率也将减小。然而Ke、Kec对动态性能也有影响，因此必须兼顾两方面的性能。

（3）当Ke=7，Kc=20时，不同的Ku时的系统响应图

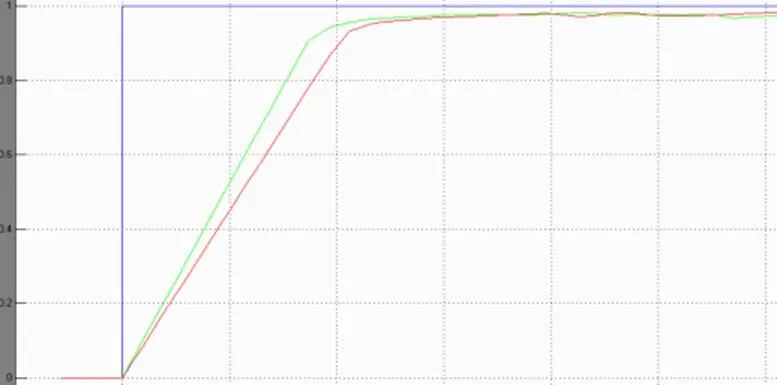
图13 Ku对控制器性能的影响

图13可中绿线为Ku较大时的仿真曲线，可以发现Ku对系统的影响比较复杂，可分为上升阶段和稳定阶段，在上升阶段，Ku越大，上升越快，超调量增大，响应时间减小，Ku小，则系统的反应比较缓慢；稳定阶段，Ku过大易引起振荡和发散。一般Ku不影响系统的稳态误差。

量化因子和比例因子的选择并不是唯一的，可能有几组不同的值都能使系统获得较好的响应特性。对于比较复杂的被控过程，有时采用一组固定的量化因子和比例因子难以收到预期的控制效果，可以在控制过程中采用改变量化因子和比例因子的方法来调整控制过程中不同阶段上的控制特性，使其对复杂过程控制受到良好的控制效果。

2.4 控制对象结构对系统动态性能的影响

在系统动态性能较好的前提下，保持系统的其它参数不变，然后改变系统的控制对象，即传递函数，研究控制对象结构对系统性能的影响。

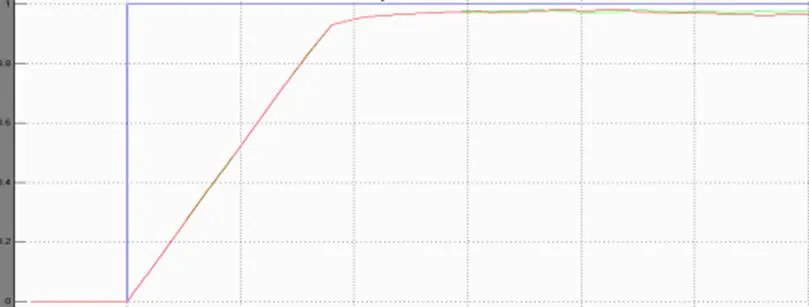
图14 控制对象结构为不同阶时对控制器性能的影响

从图14可以看出改变控制对象由一阶改为二阶，用相同的模糊控制器，输出结果的差别很小，高阶的传递函数更逼近原始波形。

（2）同样保持系统的其它参数不变，使模糊控制器1的传递函数为H(S)=250／(300S+1),模糊控制器2的传递函数为H(S)=270∕(300S+1)仿真结果：

图15 同阶控制对象对控制器性能的影响

图15可以看出改变同阶控制对象的系数，用相同的模糊控制器，输出结果的差别依然很小，系数大的传递函数更逼近原始波形，不过有点振荡。

2.5 模糊规则的数量对系统控制性能的影响

模糊控制器能得到广泛的应用，是因为它能实现基于语言的控制规则。现选取两个均为双输入单输出的模糊控制器，两个模糊控制器的误差的基本论域为E=[-1,1]、误差变化率的基本论域为 EC=[-0.1,0.1]和输出控制量的基本论域为UC=[-2, 2]，两个模糊控制器的其它参数完全相同，模糊控制器1规则的条数为5条，给模糊控制器2规则的条数加为6条，研究其对系统动态性能的影响。

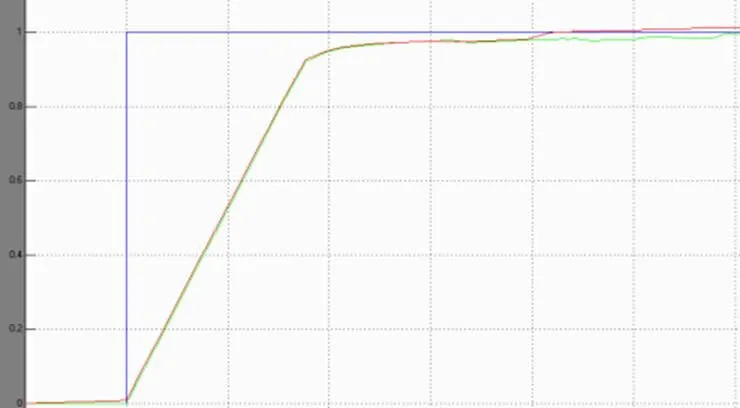
图16 不同规则数量对模糊控制器性能的影响

从图16可以看出用相同的模糊控制器，输出结果规则条数多的模糊波形更逼近原始波形，可以得出，划分的越细，规则条数越多，控制精度越高。实际上控制规则的条数要合理，条数太少，则控制是不完全和粗糙的。同样条数也不能太多，如果条数太多，则会出现功能相近的规则，造成处理上的麻烦和推理的时间消耗。

3 结束语

参数的选择对模糊控制器动态性能有较大的影响，因此在进行控制参数选择时，应充分考虑它们对模糊控制器动态性能的影响，选择一组最合适的控制参数和比例（量化）因子，有时甚至要根据系统的实际要求，在线优化、调整参数，从而获得最佳的控制效果。

[1] 陈伯芳,尹平林,马虎.基于模糊神经网络的温度控制系统研究[J].计算机与数字工程,2010,38(7):54-57.

[2] 张弘.大滞后系统控制中专家-模糊PID方法的应用[J]. 计算机工程与应用，2009，45(28):244-245.

[3] 马长华,朱伟兴.比例因子对模糊控制器动态性能的影响[J]. 江苏理工大学学报，2000,21(5):87-90.

[4] 周李涌,高丽丽.论模糊控制器中量化因子和比例因子的作用[J].内蒙古科技与经济, 2004(19):61-62.

[5] 张立,胡玉贵.量化因子和比例因子在模糊控制器中的作用及其在线修正[J].移动电源与车辆,2008(1):11-14.

[6] 林小锋,廖志伟.隶属函数对模糊控制性能的作用与影响[J].电机与控制学报,19982(4):197-200.

[7] 陆哲明,姜守达,董寒丽.基于人类视觉系统的自适应水印嵌入算法[J].哈尔滨工业大学报,2003 ,35(2):138-141.

[8] 丁广东,罗永健,丁小勇,等.一种基于模糊控制的图像水印新算法[J].计算机与数字控制，2010,38(1):151-154.

[9] 朱磊. 基于模糊控制规则的队列接入控制方案[J].计算机工程，2009,35(15): 106-107.

The Effects of parameter on the Dynamic Performance of Fuzzy Controller

*KONG Cui-xiang，LIAO Ping

(School of Electronic and Information Engineering, Jinggangshan University, Ji’an, Jiangxi 343009,China )

Thedynamic performance of the fuzzy controller is an important index. It is very important to select the parameter of fuzzy controllerduring the design of fuzzy controller. We propose a simulation model of the system, which is used to simulate and analysisthe effects of parameter on the dynamic performance of fuzzy controller based on Matlab. The results of the simulation show that the fuzzy controller can play the best performance only selecting a set of optimization parameters.

fuzzy controller; parameters; dynamic performance; simulation

TP273.04

A

10.3969/j.issn.1674-8085.2012.02.016

1674-8085(2012)02-0063-05

2011-12-24；

2012-01-18

*孔翠香(1978-)，女，陕西渭南人，讲师，硕士，主要从事自动控制，无线传感器网络等研究(E-mail: liuyun8888@163.com);

廖 萍(1980-)，男，湖南衡阳人，讲师，主要从事计算机应用研究(E-mail: jxjgsliaoping@163.com).