变分数阶微积分在描述材料力学性质演变方面的应用

李彦青 殷德顺 吴 浩

（河海大学 力学与材料学院，南京 210098）

最近，分数阶微积分正在被广泛地应用于粘弹性材料的研究中［1－4］.人们发现分数阶本构模型具有参数少、形式简单等优点，并且模型中的参数可以指代材料力学性质，使定量描述力学性质成为可能.但是常分数阶中阶数是不变的，不考虑力学性质随时间变化的情况，而在实际中，材料在受力过程中，力学性质是随时间变化的，这意味着在受力过程中阶数也应该是随时间变化的，这就需要考虑采用变分数阶模型来定量描述材料力学性质的变化情况.

变分数阶微积分本构模型也开始引起广大研究者的兴趣［5］，变分数阶微积分是分数阶微积分的最新发展，它的阶数不但不再是整数而且可以随时间或空间变化，即可以是一个变量.所谓变分数阶模型就是希望通过阶数的变化来描述变形过程中力学性质的演变.这一方面的研究在国际上刚刚起步，还没有引起国内学者的重视，本文希望建立变分数阶本构模型，可以定量描述粘弹性材料力学性质演变.

本文在常分数阶本构模型的基础上提出了变分数阶本构模型.从理论上讲，可以通过变分数阶阶数的变化来展示材料力学性质的变化，但其结果是否可靠是个问题.通过对塑性金属铜、铝、低碳钢进行了一系列的等应变率加载试验，并用本文所提的变分数阶本构模型进行分析，探求其在受力过程中力学性质的演变与实际是否相符，以此来验证该模型是否可以用来描述材料力学性质演变.

本文所研究的阶数的变化范围为0到1，所以该模型也可用于其他粘弹性材料在具有时间效应的受力及变形过程中力学性质演变的分析，如岩土及高分子材料的应力松弛与蠕变，等应变率加载等.之所以选择金属作为研究对象是因为：①固体力学理论来源于塑性金属；②塑性金属性质稳定，而且对于金属的性质研究较为透彻.

1 变分数阶微分简介

变分数阶微积分是在常分数阶微积分的基础上发展起来的，目前对于变分数阶有很多定义［5－9］，而阶数α（t，τ）一般有3种形式［10］：α（t，τ）＝α（t），α（t，τ）＝α（τ），α（t，τ）＝α（t－τ）.而第1种形式没有阶数记忆性，第2种形式具有较弱的阶数记忆性，第3种形式具有较强的阶数记忆性.所谓阶数记忆性是指历史时间点的阶数计算结果对当前时间的计算结果有影响，而记忆性强弱是由阶数改变产生的影响大小决定的.在本文中采用第3种形式.

本文采用Caputo型分数阶微分理论算子，对函数f（t）的α（t）阶积分在α（t，τ）＝α（t－τ）时的定义为

当f（t）＝at时，令公式（1）中的t－τ＝x，则公式（1）变为

将公式（2）写成叠加的形式，叠加形式所表示的物理意义则可由图1来说明.令g（tk，αk）＝），则可得

公式（3）中的a（t）按照表1变化.

表1 阶数α（t）的取值

图1为叠加形式的变分数阶函数物理意义的示意图.图1中的黑实线为新的变分数阶微分，虚线为阶数分别为α1、α2、α3的常分数阶微分.从图中可以看出黑色实线是由常分数阶部分曲线平移组成.图1（a）中，按时间的先后顺序，阶数的顺序为α1、α2、α3，如果顺序变为α2、α1、α3，则变分数阶就为图1（b）.通过图1（a）与（b）的对比可以发现，虽然t2到t3的阶数都为α3，但是由于0到t2之间的阶数不同，导致变分数阶的结果不同.由此可以看出新的变分数阶对阶数有记忆性，再者新的变分数阶由常分数阶微分直接拓展而来，与常分数阶有直接的联系，因此可以认为这个定义比较适合将要建立的本构模型.

图1 叠加算法的物理意义示意图

2 变分数阶本构模型

2.1 常分数阶本构模型

介于理想固体与理想流体之间的材料的本构方程可以用Smit和De Vries［11］提出的“中间模型”来描述

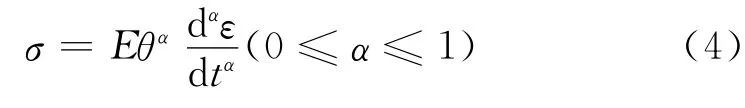
式中，E、θ、μ均为材料常数.当α为常数时，材料的力学性质不发生改变，因此这个模型被称为常分数阶模型.

公式（4）的分数阶本构模型能够将力学性质看作一个序列，理想固体和牛顿流体位于序列的两端.在一系列的参数α中，不同的α代表了材料不同的力学性质.这个模型最主要的创新点在于它可以将材料的力学性质在理想固体和牛顿流体之间找到确切的定位，如图2所示.

图2 材料力学性质划分

当公式（4）中的ε＝αt时，即等应变率加载时，公式（4）可变形为

由公式（5）可得，在等应变率加载过程，应力逐渐增大，常分数阶模型可描述等应变率加载过程中应力与应变的关系曲线.但是公式（5）所提模型中的阶数为常数，意味着材料的力学性质在等应变率加载过程中均保持不变，而这显然与实际不符，因此有必要探讨采用变分数阶微积分理论，考虑材料在变形过程中力学性质的变化.

2.2 变分数阶本构模型

在常分数阶本构模型中，阶数指代材料力学性质，对于材料性质的认识从定性认识变为定量认识，但是仍然不能定量描述力学性质变化过程，因此在这里考虑建立变分数阶本构模型.

Ingman［2］和Samko［5］曾经提出

因为，式中，E 量纲是［应力］［时间］α（t），所以，其物理意义是不确定的.另外，这个变分数阶模型仍然不能反映材料力学性质演变.

本文认为正确的模型应该为

与公式（4）类似，公式（7）中的力学参数都有明确的物理意义.

在等应变率加载情况下，根据公式（2），则公式（7）写为

公式中的，a为应变率.

根据分数阶模型的物理意义，初始阶数α1＝0，在实验曲线达到水平状态时，材料力学性质为牛顿流体，此时阶数为1.因此参数E可以由前几个线性状态下的实验点得到：

这里，σ1和ε1为材料处于弹性阶段的应力应变数值.参数θ的值为

3 塑性金属拉伸时的力学性质演变

在这节中将用变分数阶本构模型对塑性金属在等应变率拉伸时的力学性质演变进行分析、研究，以此来检验模型是否可以用来描述材料力学性质演变.

3.1 塑性金属试验介绍

这里对3种金属，包括铜、低碳钢和铝合金，进行了等应变率拉伸试验.试验样品的直径为10mm，长度分别为50mm、100mm.拉伸试验分为两组，每组3次.两组拉伸时的应变率不同：铜为0.000 133／s和0.001 33／s；低碳钢为0.000 1／s和0.001／s，铝合金为0.000 2／s和0.00 2／s.

3.2 试验数据及分析

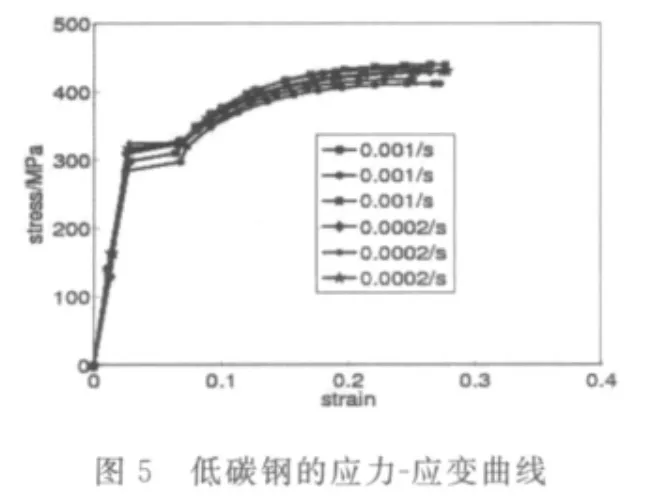
图3～5为上述金属试件拉伸试验的应力－应变结果.通过这些曲线可以发现，在加载初期，试件呈现出固体力学中的弹性状态，但是一旦超过这个阶段的极限，材料性质发生突变，而后进入非线性阶段，很明显在整个加载过程中材料的性质是不断变化的.图3显示应变率对铜有明显的影响，而从图4与图5中可以看出，铝合金和低碳钢对应变率的依赖性比较弱.

图3 铜的应力－应变曲线

基于公式（8），当铜的应变率为0.000 133／s时，其应变－阶数曲线如图6所示.由于阶数可以刻画材料的力学性质，因此，可以根据图6来描绘铜在加载过程中性质的变化过程.由图6可以看出整个力学性质的变化过程可以分为3个阶段：第1阶段，阶数为0，是线弹性阶段；在第2阶段，阶数发生突变，对应于材料晶格错位，材料性质发生突变；第3阶段，阶数按近似线性均匀变化，材料的力学性质也均匀变化.并且将第3阶段的阶数－应变进行线性拟合，再回代到上述本构模型中，在图7中给出了拟合曲线与试验点的比对图.可以发现，变分数阶模型的阶数变化可以描述材料力学性质的演变过程.

上述结论仅仅是对铜在等应变率拉伸过程中力学性质演变一个分析，对于其他的金属材料是否会得到类似的结论，需要对其他金属材料的试验数据进行分析，因此本文对低碳钢和铝合金也做了计算对比.

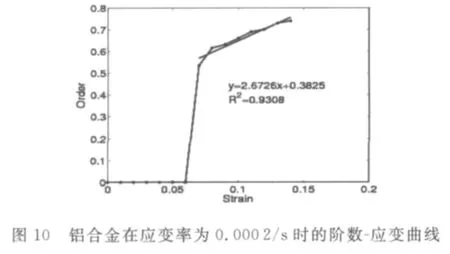
图8～11中给出的是，试验的应变率分别为0.000 1／s（低碳钢）和0.000 2／s（铝合金）的试验数据处理结果.在低碳钢的试验中，低碳钢的晶格错位明显，力学性质在第二阶段特别明显，而变分数阶模型的阶数在这一阶段的突变也很明显，与之对应，再次证明了模型是可信的.

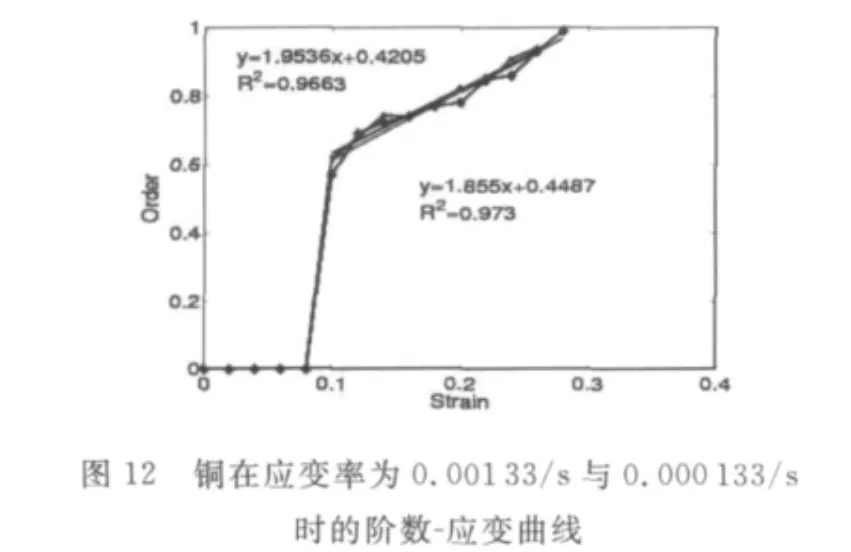
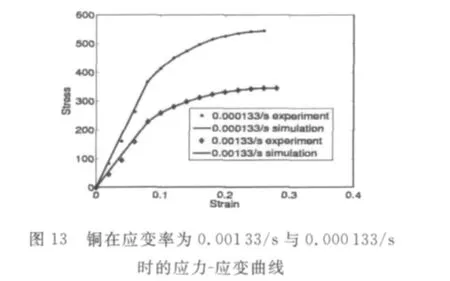
在不同的应变率加载情况下，金属材料的力学性质演变是否会受到应变率的影响，也是需要进行探讨.在这里，对同种金属材料在不同应变率下的试验数据进行了对比分析.图12给出的是，铜在应变率分别为0.000 133／s和0.001 33／s时的阶数－应变曲线，可以发现两条阶数－应变曲线的走势几乎相同.从图14（应变率分别为0.000 2／s和0.001／s）低碳钢的试验及分析中也可以发现这一现象.这进一步说明，变分数阶模型可以用来描述塑性金属力学在不同应变率情况下的性质演变，并且在等应变率加载条件下，塑性金属力学性质演变基本不受应变率的影响.

通过上述金属的试验验证，说明了变分数阶本构模型是可以用来定量描述力学性质演变的.并且在等应变率加载过程中，可以认为金属材料的性质变化可以分为3个阶段，第1个阶段为线弹性阶段；第2阶段，材料从弹性变为塑性的过程称为屈服阶段，在这一阶段金属的晶格进行错位，力学性质产生突变，这与实验相吻合；第3阶段，力学性质按线性变化.这些数据有力地说明了变分数阶本构模型是可以用来定量描述力学性质演变的.另外加载时的应变率对同种金属材料的力学性质演变基本没有影响.

4 结 论

在常分数阶本构模型的基础上提出了可以描述力学性质演变的变分数阶本构模型.并用金属材料试验进行了验证，发现该模型的阶数能够定量描述塑性金属力学性质的演变.

用本文提出的变分数阶模型对铜、铝合金、低碳钢在等应变率拉伸时的试验数据进行处理后发现，阶数－时间曲线的变化可以分为3个阶段，对应力学性质的变化也可以分为3个阶段：第1阶段，力学性质保持不变，为线弹性阶段；第2阶段，对应拉伸过程中晶格错位，力学性质发生突变；第3阶段，力学性质按线性变化阶段.在等应变率加载条件下，金属力学性质变化基本不受应变率影响.

在本文中所研究的等应变率试验中，应力－应变关系曲线都达到一个极值点，而对于实际中未达到极值点的情况，则可以根据在第3阶段中力学性质按线性变化这一点，对相应的应力或应变进行预测.

另外，因为该模型阶数的变化范围为0到1，所以该模型可用于其他粘弹性材料在具有时间效应的受力及变形过程中力学性质演变的分析，如岩土及高分子材料的应力松弛与蠕变，等应变率加载等.在此，笔者只是对一维的变分数阶本构模型进行了分析，对于三维模型的建立，还需要进行更深入的研究.

［1］ Nicole Heymans.Dynamic Measurements in Long－memory Materials：Fractional Calculus Evolution of Approach to Steady State［J］.Journal of Vibration and Control，2008，14：1587－1596.

［2］ Ramirez L E S，Coimbra C F M.A Variable Order Constitutive Relation for Viscoelasticity［J］.Annalen der Physik，2007，16（7）：543－552.

［3］ Ingman D，Suzdalnitsky J.Application of Differential Operator with Servo－order Function in Model of Viscoelastic Deformation Process［J］.Journal of Engineering Mechanics，2005131（7）：763－767.

［4］ Soon C M，Coimbra C F M，Kobayashi M H.The Variable Viscoelasticity Oscillator［J］.Annalen der Physik，2005，14（6）：378－389.

［5］ Samko S G，Ross B.Integration and Differentiation to a Variable Fractional Order［J］.Integral Transforms and Special Functions，1993，1（4）：277－300.

［6］ Mandelbrot B B.The Fractal Geometry of Nature［M］.New York：W.H.Freeman and Company，1982.

［7］ Coimbra C F M.Mechanics with Variable－order Differential Operators［J］.Annalender Physic，2003，12（11）：692－703.

［8］ Ingman D，Suzdalnitsky J.Control of Damping Oscilla－tions by Fractional Differential Operator with Time－dependent Order［J］.Computer Methods in Applied Mechanics and Engineering，2004，193（52）：5585－5595.

［9］ Ingman D，Suzdalnitsky J，Zeifman M.Constitutive Dynamic－order Model for Nonlinear Contact Phenomena［J］.Journal of Applied Mechanics，2000，67（2）：383－390.

［10］Lorenzo C F，Hartley T T.Variable Order and Distributed Order Fractional Operators［J］.Nonlinear Dynamics，2002，29（4）：57－98.

［12］Smit W，de Vries H.Rheological Models Containing Fractional Derivatives［J］.Rheologica Acta，1970，9（4）：525－53.