基于F分布的无线传感器网络攻击检测方法

史德阳，罗永健，侯银涛，张卫东

（西安通信学院电子工程系，陕西西安 710106）

为了减少冗余数据的传输，无线传感器网络（wireless sensor networks，WSN）通常采用聚合函数对节点感知数据进行汇聚处理，但汇聚安全问题严重限制了数据汇聚技术的推广应用［1］。目前，针对数据汇聚的攻击行为主要有2种［2］：第1种是在数据从源节点到汇聚节点的传输过程中进行，应对这类攻击的安全措施是采用常规的加密认证技术［3］，目前这方面技术的发展比较成熟；第2种是控制节点感知环境或者俘获汇聚所使用的部分节点，对其重新进行编程，篡改其读数。针对此类攻击，通常采取的方法是先采用攻击检测算法对所要汇聚的数据进行检测，判断是否有攻击行为，如果没有就直接汇聚，如果有就采取相应的数据复原汇聚算法进行汇聚处理［2］。

目前第2类安全威胁已引起高度关注［4］，但针对此类攻击的检测算法的研究在国内外开展还较少。BUTTYAN等最早提出二分比较法（split and check，SC）［5］，该算法建立在集中式数据汇聚模型的基础上，对网络的能量消耗较大，且攻击检测率较低。为了降低能耗，根据WSN均匀分簇和非均匀分簇2种情况，文献［6］提出了2种基于分簇模型的卡方检验攻击检测算法，在能耗和检测性能方面较二分比较法有明显改善，但攻击检测率仍然较低。SHU等提出一种基于密集数据挖掘的数据复原汇聚算法［7］，该算法采用信息挖掘技术，对节点感知数据进行过滤，可以实现相对精确的平均值汇聚，但在WSN中不存在攻击时该算法仍会剔除边缘数据。为了克服上述不足，文献［8］提出一种基于t分布的WSN攻击检测算法，该算法对感知数据先验信息的要求较少，但该算法的攻击检测率与参考簇的选取有关，当参考簇选为不受攻击或受攻击较弱的簇时，其检测效果不太理想。基于此，提出一种基于F分布的WSN攻击检测方法。

1 攻击检测模型

文中算法建立在分布式数据汇聚模型的基础之上，其具体模型如图1所示。首先利用分簇算法将无线传感器网络划分为若干个簇，每个簇含有若干个传感器节点并选择其中一个节点充当簇头。簇头收集所在簇节点的感知数据并进行汇聚处理，然后将汇聚结果通过单跳或多跳路由传送至基站。基站是一个特殊的节点，对从簇头传送过来的数据利用攻击检测算法进行检测。当检测不存在攻击时利用聚合函数直接进行汇聚，否则，采用相应的数据复原汇聚算法进行汇聚处理。最后，基站将最终的汇聚结果通过Internet、移动通信网络、卫星等与监控中心进行通信。

在上述分布式数据汇聚模型的基础上，文中算法作如下假设。

1）基站是足够安全的，攻击者只能对普通传感器节点进行攻击。由于基站通常采用较强的防护措施，故不易受到攻击。而传感器节点是一种价格低廉、结构松散、开放的网络设备，极易受到恶意攻击［9］。

2）节点攻击方式为加性攻击［5］。加性攻击有增量攻击和常量攻击2种，对每个被俘获节点读数都增加一个相同值即为增量攻击，修改被俘获节点读数使其达到同一个值即为常量攻击。

3）被俘获节点的分布相对集中。攻击者往往是根据条件在操作方便的范围内选择节点进行攻击，而不能随意在网络中选择，故假设被俘获节点相对集中于网络中的某些簇是合理的。

4）被俘获节点的数量有限。若攻击者有足够的能力可以在网络中任意选择节点进行攻击，则所有的攻击检测算法都将失去作用。

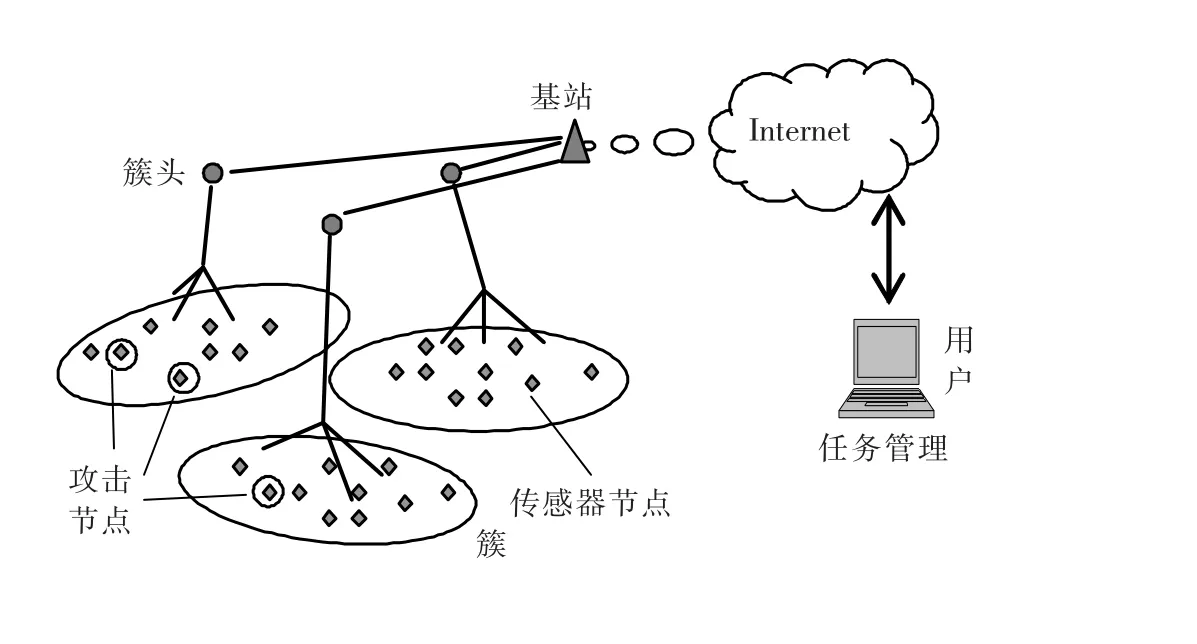
图1 分布式数据汇聚模型Fig.1 Distributed model of data aggregation

2 基于F分布的WSN攻击检测方法

为了表述方便，特定义以下符号。

n：WSN中节点的总数目；r：WSN中分簇的数目；Ci：WSN的第i个簇；mi：簇Ci中所含节点的数目；：簇Ci中第j个节点的读数；¯Xi：簇Ci中节点读数的平均值；α：显著性水平，在文中的含义为虚警率；K：受攻击节点数目。

令簇Ci中节点感知数据服从期望值为μi（i=1，2，…，r）、方差为σ2的正态独立同分布。检验H0：μ1=μ2=…=μr；H1：μ1，μ2，…，μr不全相等。当无线传感器网络没有遭受攻击时H0成立，否则H1成立。

由于未遭受攻击的传感器节点读数服从独立同分布，根据中心极限定律，簇Ci中各传感器读数之和Yi服从高斯分布，即

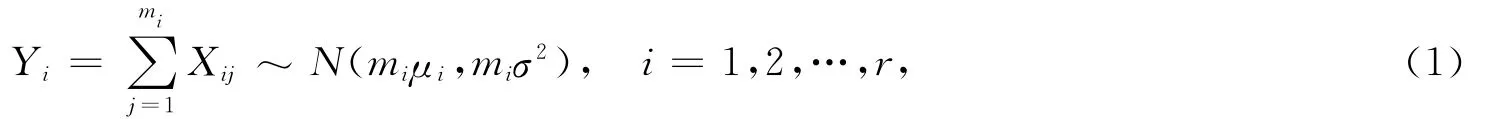
则簇Ci中样本数据的平均值¯Xi服从分布

上海诚达物流作为第三方运输公司，提供专业的第三方运输服务。但与运输相关的其他第三方物流服务并有涉及，导致了上海诚达物流公司服务产品的单一性。

基站对接收到的各簇均值进行比较，选择均值最大的簇作为Cz。当i≠z时，¯Xi与¯Xz相互独立，由高斯分布的性质可知：

由于V1，V2，…，Vr（i=1，2，…，r，i≠z）独立同分布于标准正态分布，有

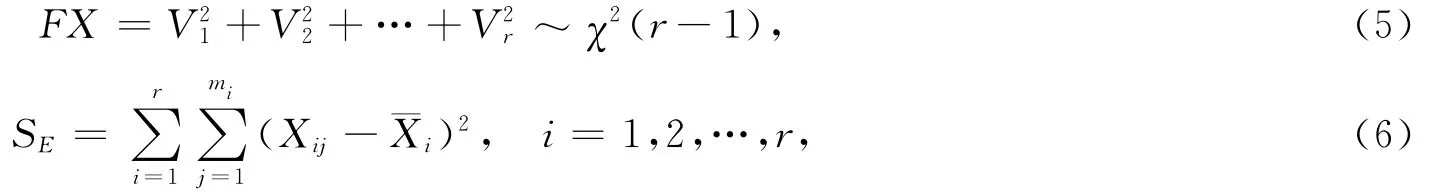
其中，SE为组内偏差平方和。

在簇Ci中，感知数据的样本方差为

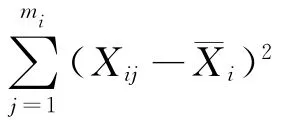
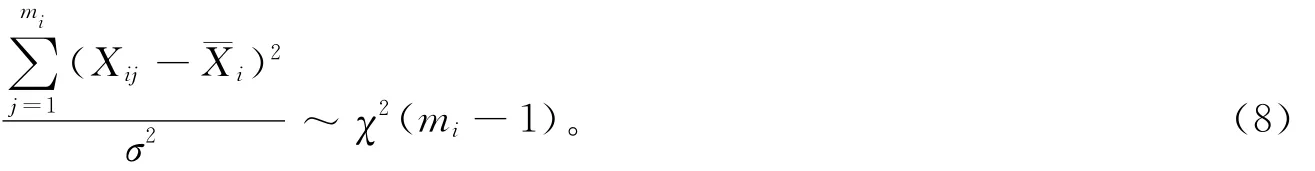
又因Xij独立同分布，所以式（6）中各平方和项均相互独立。由χ2分布的相加性可得：

由于FX和FY分别服从自由度为（r-1）和（n-r）的χ2分布，且FX和FY相互独立，由F分布的定义知［10］：

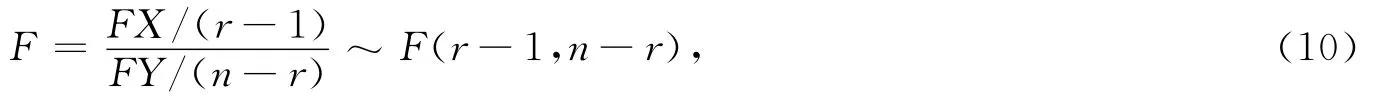
将式（5）、式（9）代入式（10）得：

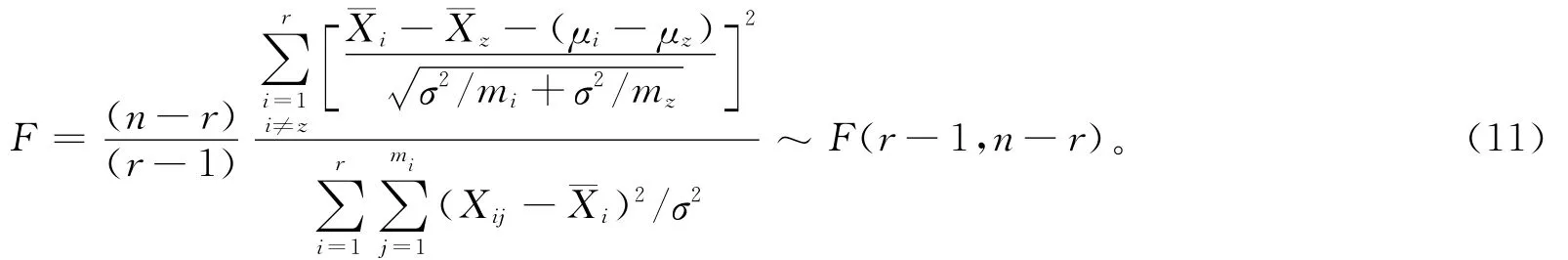
将μ1=μ2=…=μr代入式（11）并化简得假设检验H0的统计量为

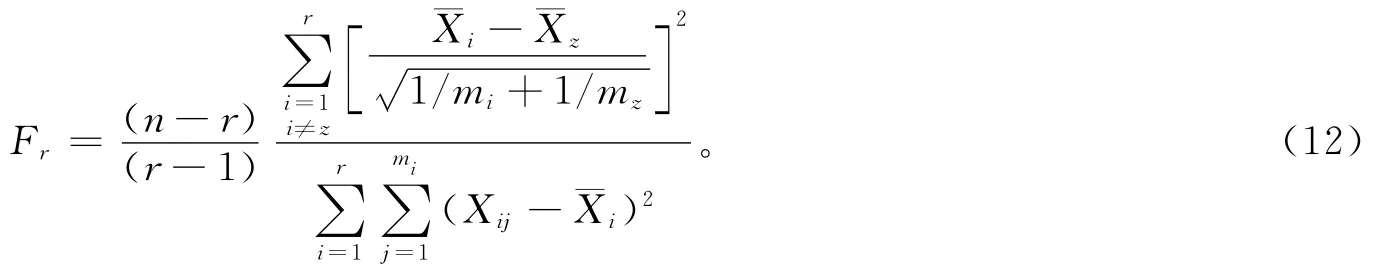
故虚警率恒为α时的拒绝域为

式中，Fα（r-1，n-r）为F（r-1，n-r）上的α分位点。

将WSN各簇感知数据代入式（12），若求得的结果满足式（13），则认为假设H0不成立，即传感器网络中存在攻击，反之，则认为网络中不存在攻击。

与二分比较法［5］、卡方检验法［6］和t检验法［8］相比，新算法有以下优点。

1）由式（12）可以看出，新算法不仅考虑了簇间均值的差异，还考虑了组内偏差平方和，而二分比较法仅通过判断残差的期望是否为零来检测攻击，卡方检验法也只考虑了组内偏差平方和，所以新算法的检测率更高。虽然新算法与t检验法考虑的因素相同，但与t检验法的攻击检测公式相比，新算法放大了簇间均值差异的影响，而弱化了组内偏差平方和的影响。

2）新算法采用了分簇模型，较二分比较法能获得较低能耗。对于均匀分簇和非均匀分簇，式（12）均适用，而卡方检验法在均匀分簇和非均匀分簇情况下的检测公式不同，计算复杂度较高。

3）新算法要求的先验信息较少，不需要感知数据的期望和方差信息，而二分比较法和卡方检验法都要求方差已知。

3 性能仿真

将100个传感器节点随机部署在100m×100m的区域内，为方便考虑，假定在WSN中不存在攻击时，节点感知数据服从标准正态分布，且虚警率α=0.05。由于二分比较法和t检验法都只对增量攻击进行了讨论，文中在增量攻击下将新算法与二分比较法和t检验法进行Matlab仿真实验对比。计算机仿真中均进行2 000次的蒙特卡洛实验。

考虑聚合函数为求均值的情况，当有K个节点遭到攻击时，攻击者对数据汇聚结果所造成的偏差为

式中：d为攻击所造成的偏差；ΔA为攻击增量。

3.1 新算法与二分比较法的性能比较

在WSN中，非均匀分簇的应用较为广泛，所以文中对非均匀分簇下的新算法和集中式数据汇聚模型下的二分比较法进行了仿真对比。将网络划分为节点数分别为10，15，20，25，30的5个簇，此时门限值Fα=2.467 5。

图2为K=2和K=19时新算法与二分比较法的仿真结果对比。当K=2和K=19时，新算法的攻击检测率较二分比较法有明显提高，这是因为新算法综合考虑了簇间均值差异及组内偏差平方和的影响，而二分比较法仅考虑了两部分数据的残差。在K=2时二分比较法的检测率收敛于0.5，而无法收敛于1。仿真实验表明，当受攻击节点数为偶数时二分比较法的攻击检测率都无法收敛于1，因为若等分的两部分数据所包含的受攻击节点数相等时，两部分数据的残差的期望将为零。而新算法则不存在这种问题，能够弥补二分比较法的这一缺陷。

图2 新算法与二分比较法的性能对比Fig.2 Comparison between the new algorithm and SC

3.2 新算法与t检验法的性能比较

笔者针对无线传感器网络非均匀分簇和均匀分簇2种情形对新算法进行仿真实验，并在相同实验条件下与t检验法进行了对比分析。由于t检验法的检测率与参考簇的选取有关，且在参考簇选为受攻击簇时的检测率较高，本文只对t检验法的参考簇选为受攻击簇时与新算法进行了仿真对比。

3.2.1 非均匀分簇时的仿真比较

将无线传感器网络划分为节点数分别为10，15，20，25，30的5个簇，此时门限值Fα=2.467 5。

图3为K=9和K=35时攻击检测率随偏差变化的仿真结果。当K=9时，新算法的检测效果略好于t检验法；当K=35时，新算法的攻击检测率明显高于t检验法。与t检验法相比，新算法放大了簇间均值差异的影响，并弱化了组内偏差平方和的影响。当网络中对某些簇的攻击达到饱和（即该簇有半数以上的节点遭到攻击）时，组内偏差平方和会使算法的攻击检测率降低［8］，所以新算法的攻击检测率较高。

图4为攻击增量为2时攻击检测率随受攻击节点数K变化的仿真结果。当攻击增量为2时，K＜10时新算法的检测率稍高，10≤K＜30时两者的检测率相当。当K≥30时，受组内偏差平方和的影响，t检验法的检测率下降，而新算法的检测率则稳定于1。

图3 非均匀分簇ΔA变化时新算法与t检验法的性能Fig.3 Comparison between the new algorithm and t-test algorithm（ΔAis variable and the network is un-uniform）

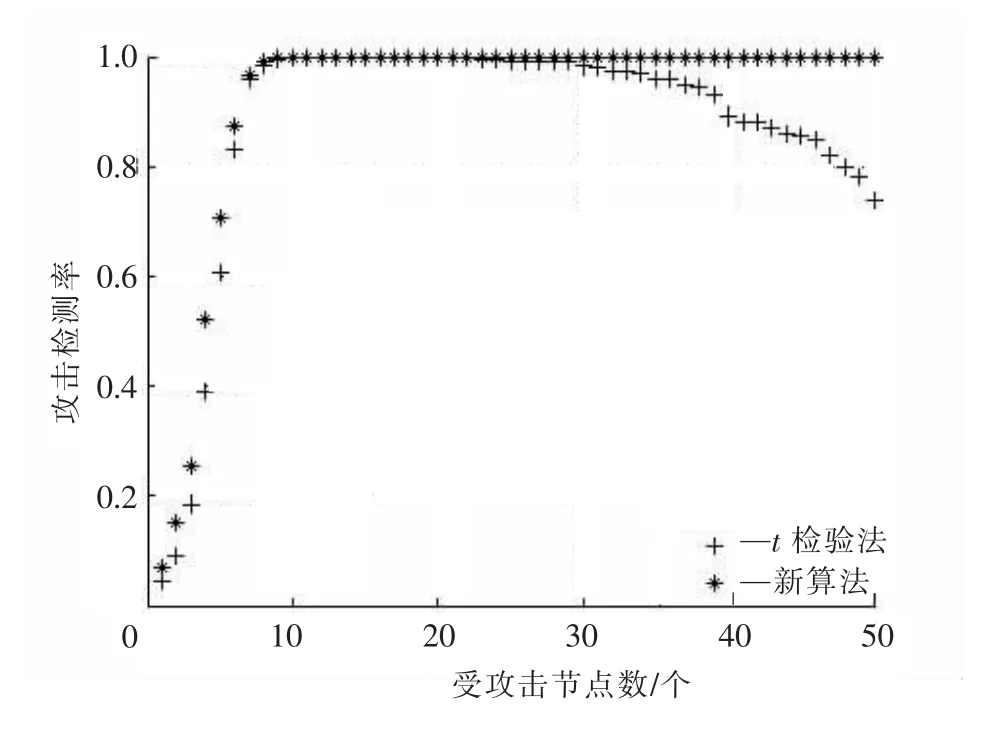
图4 非均匀分簇K变化时新算法与t检验法的性能对比Fig.4 Comparison between the new algorithm and t-test algorithm（Kis variable and the network is un-uniform）

在非均匀分簇时，当攻击节点数K=16时新算法与t检验法的抗噪声性能对比如图5所示，新算法在信噪比为0dB和-5dB时的攻击检测率都要高于t检验法，故新算法对网络噪声干扰的稳健性要强于t检验法。

3.2.2 均匀分簇时的仿真比较

将WSN均匀划分为10个簇，各簇节点数均为10，求出门限值Fα=1.985 6。

图6为K=2和K=45时攻击检测率随偏差变化的仿真结果。由图6可知，当WSN均匀分簇时，K较小时新算法的检测效果略好于t检验法，K较大时新算法的攻击检测率明显高于t检验法。在同一偏差下，如偏差为0.2时，新算法在K=2时的检测率为1，K=45时的检测率则为0.2，K越大检测率反而越低。这是因为要达到同一偏差，新算法在K较小时，对受攻击节点施加的攻击增量越大；且K值越小越易把受攻击的节点集中在较少的簇中，而值越大受攻击节点的分布则可能越分散。

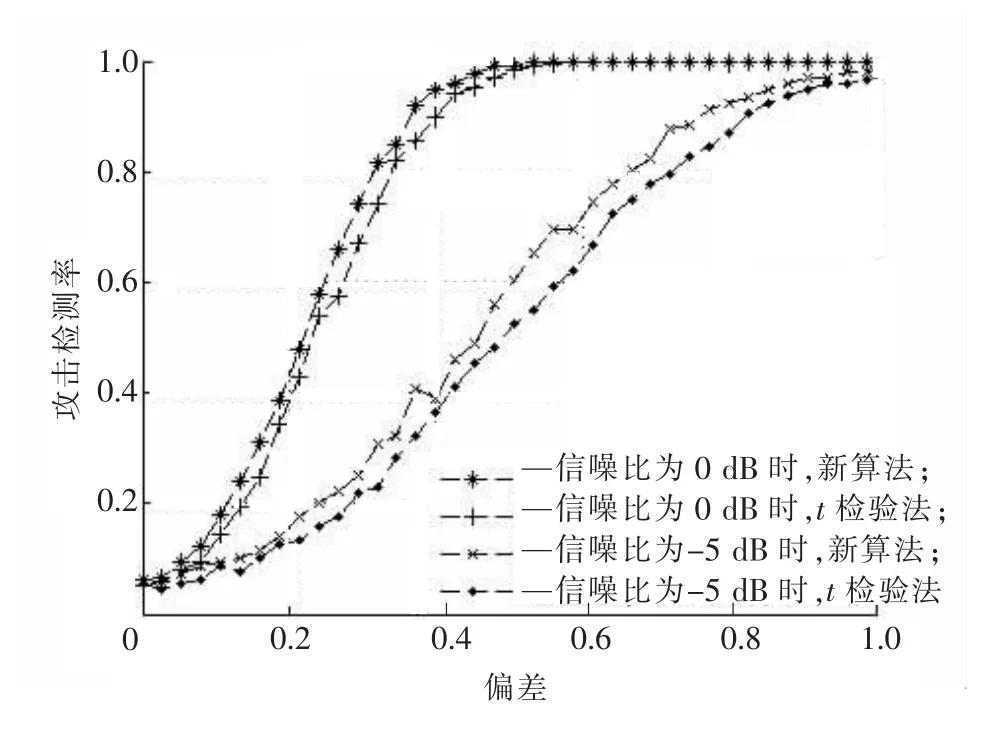
图5 非均匀分簇时新算法与t检验法的抗噪声性能Fig.5 Comparison of performance against noise jamming between the new algorithm and t-test algorithm when the network is un-uniform

图6 均匀分簇ΔA变化时新算法与t检验法的比较Fig.6 Comparison between the new algorithm and t-test algorithm（ΔAis variable and the network is uniform）

在均匀分簇的情况下，K=16时新算法与t检验法的抗噪声性能对比如图7所示，新算法在信噪比为0dB和-5dB时的攻击检测率都要高于t检验法，这是因为新算法通过增大簇间均值在攻击检测时所占的比例来降低噪声影响，新算法对网络噪声的稳健性要优于t检验法。

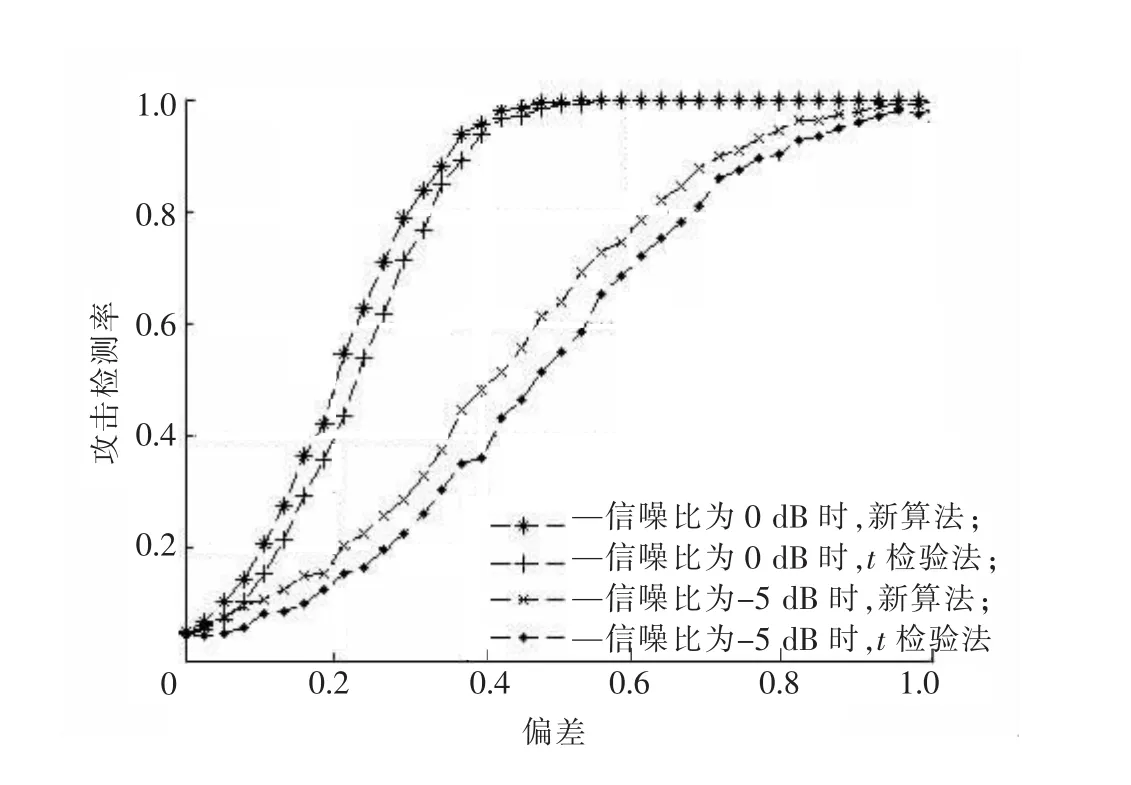
图7 均匀分簇时新算法与t检验法的抗噪声性能Fig.7 Comparison of performance against noise jamming between the new algorithm and t-test algorithm when the network is uniform

4 结 语

针对现有WSN攻击检测算法存在的不足，提出了一种基于F分布的无线传感器网络攻击检测方法。该方法对传感器节点感知数据的先验信息要求较少，攻击检测率较高，且对网络噪声干扰的稳健性较强。理论分析和实验仿真结果表明，文中算法的攻击检测性能要优于现有的攻击检测算法。下一步的研究重点是搭建无线传感器网络实验平台，对新方法在实际无线传感器网络中的应用效果进行验证。

［1］ 罗永健，丁小勇，罗相根，等.一种有效的无线传感器网络数据复原汇聚方法［J］.数据采集与处理（Journal of Data Acquisition and Processing），2011，29（1）：90-94.

［2］ WAGNER D.Resilient aggregation in sensor networks［A］.Proceedings of the 2nd ACM Workshop on Security of Ad Hoc and Sensor Networks［C］.Washington D C：ACM New York Press，2004.78-87.

［3］ ZIA T，ZOMAYA A.A security framework for wireless sensor networks［A］.Proceedings of the 2006IEEE Sensors Applications Symposium［C］.Houston：IEEE，2006.49-53.

［4］ HAOWEN C，ADRIAN P，DAWN S.Secure hierarchical in-network aggregation in sensor networks［A］.Proceedings of CCS’06［C］.Virginia：ACM New York Press，2006.278-287.

［5］ BUTTYAN L，SCHAFFER P，VAJDA I.Resilient aggregation with attack detection in sensor networks［A］.Proceedings of the Fourth Annual IEEE International Conference on Pervasive Computing and Communications［C］.Washington D C：IEEE Computer Society Press，2006.332-336.

［6］ LUO Yong-jian，YANG Xin，ZHANG Xu.An effective resilient data aggregation algorithm in wireless sensor networks［A］.2007International Conference on Wireless Communication，Networking and Mobile Computing［C］.NJ：IEEE Press Piscataway，2007.2 642-2 645.

［7］ SHU Qin-ren，JONG S P.Density mining based resilient data aggregation for wireless sensor networks［A］.Fourth International Conference on Networked Computing and Advanced Information Management［C］.Washington D C：IEEE Computer Society Press，2008.261-266.

［8］ LUO Yong-jian，DING Xiao-yong，WU Gang，et al.A novel attack detection algorithm based ont-distribution in wireless sensor networks［A］.2009International Conference on Wireless Communications［C］.NJ：IEEE Press Piscataway，2009.1-4.

［9］ ROBERTO D P，PIETRO M，REFIK M.Confidentiality and integrity for data aggregation in WSN using peer monitoring［J］.Security and Communication Networks，2009，2（2）：181-194.

［10］ 费 宇.应用数理统计［M］.北京：科学出版社，2007.