基于AHP的纱线综合性能评价指标权重研究

李海萍，李向红

（1.河北科技大学理学院，河北石家庄 050018；2.河北科技大学纺织服装学院，河北石家庄050018）

纱线是一种多属性产品，具有多种性能测试指标，在评价纱线综合性能时，这些性能指标并不是平权的，要依据纱线的用途，确定各项评价指标的权重，进而综合评定成纱质量［1］。笔者以喷气织机用JC7.3tex纯棉赛络间接纬纱为例，运用层次分析法确定成纱性能指标的权重。

1 层次分析法

层次分析法（analytic hierarchy process，简称AHP）是美国运筹学家SAATY教授提出的一种将定性与定量相结合的分析方法，是将一个复杂的多目标决策作为一个系统，将目标分解为多个目标或准则，进而分解为多指标的若干层次。其基本思想是将构成复杂问题的多个元素权重的整体判断转变为对这些元素进行“两两比较”，然后再对这些元素的整体权重进行排序判断，最后通过定性指标模糊量化方法确立各元素的权重和总排序，以作为多指标、多方案优化决策的系统方法。层次分析法的优点是具有系统性、实用性和简捷性，定性与定量相结合，主观与客观相结合，可以增加决策的有效性［2］。

1.1 构建层次分析模型

对纱线性能测试指标进行分类，构建一个性能指标间相互连接的递阶层次结构。纱线性能综合评价体系分3层，第1层为总目标即最优纱线A，第2层为子目标B，包括成纱条干B1、成纱强力B2和成纱毛羽B3共3项，第3层为指标层C，即每项子目标下面包含的若干个指标［3］。整个纱线综合性能评价指标体系如表1所示。以下将运用层次分析法确定C1-C9这9项的权重。

表1 纱线综合性能评价指标体系Tab.1 Yarn comprehensive performance evaluation index system

1.2 构建判断矩阵

采取专家调查问卷形式，请各位专家对层次结构中各指标进行重要性排序并量化，在每一层次上，根据问卷调查结果，写出数值判断矩阵，记为A：

表2 因素i与j重要性标度及其描述Tab.2 Number scale and its description of two factors

1.3 一致性检验

表3 随机一致性指标（RI）Tab.3 Random index（RI）

2 纱线综合性能评价指标权重确定

2.1 专家1的判断矩阵及其一致性检验

根据对专家1的问卷调查结果，可得子目标B对总目标A的判断矩阵，记为A-B。

其中1行2列中的元素3表示：专家1认为在最优纱线影响因素中成纱条干B1比成纱强力B2的影响“略重要”，从表2中查得“略重要”用3表示。其他元素的含义同理。

其他判断矩阵用上述方法给出。

用上述方法可计算出所有特征值、特征向量并进行一致性检验，见表4。

表4 特征值、特征向量和一致性检验结果Tab.4 Eigenvalue，eigenvector and the consistency judgment

2.2 专家1总排序及一致性检验

层次总排序也有一致性检验，检验从高层次到低层次，假设CIj是Y层次的某因素对Xj的一致性指标，RIj是平均随机一致性指标，则总排序一致性比率为

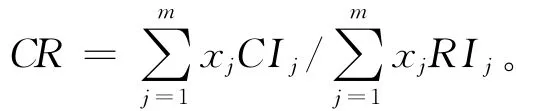
通过一致性检验。

2.3 所有专家评价的权重

根据所有专家的调查结果，构建成对比较矩阵，利用AHP软件计算最大特征根及对应特征向量，并进行一次性检验。若检验通过，归一化后的特征向量为权向量即权重；若一次性检验不通过，需要重新构建成对比较矩阵。在设计专家调查表时，为保证调查问卷的有效性，提高一致性检验的通过率，对调查的内容作了简化处理。邀请高校5位专家和邯郸圣绵纺织有限公司10位专家接受问卷调查，利用上述层次分析法可同样计算出15位专家调查结果的权重，取其平均值，作为最终评价成纱性能指标的权重，表5为成纱性能各项指标权重计算结果汇总。

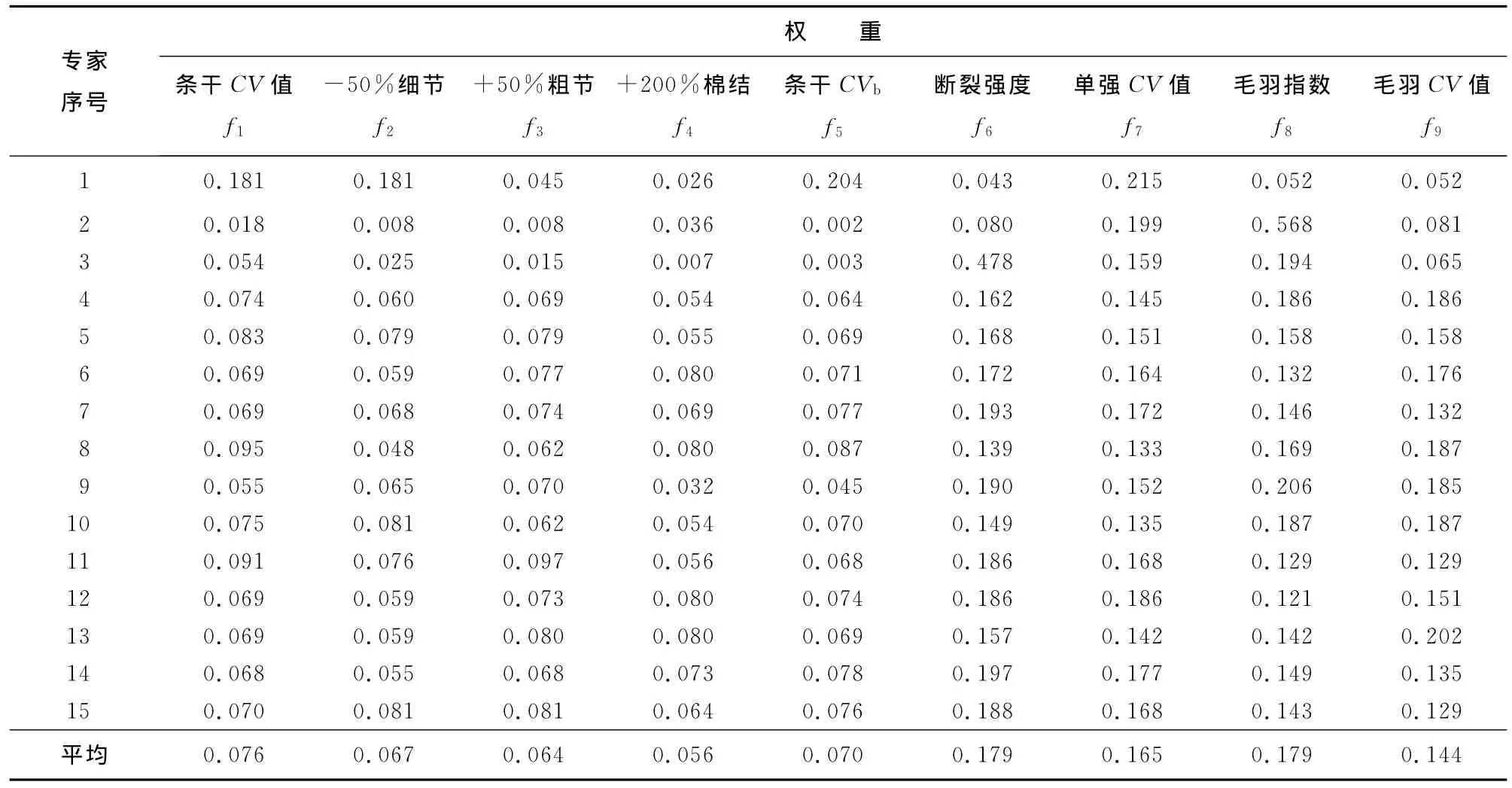
表5 成纱性能指标权重汇总Tab.5 Yarn property weights set

根据计算结果，确定评价喷气织机用JC7.3tex纯棉赛络间接纬纱各项性能指标的权重分别为f1=0.076，f2=0.067，f3=0.064，f4=0.056，f5=0.070，f6=0.179，f7=0.165，f8=0.179，f9=0.144。

3 实证分析

经实验得JC7.3tex纯棉赛络间接纬纱9种纺纱方案的纱线性能测试指标，如表6所示。下文将依据表5所示的纱线综合性能评定权重，采用加权Borda数法对9种方案进行模糊决策分析。

表6 不同纺纱方案下的成纱性能指标Tab.6 Yarn property index by different program

U=｛u1，u2，…，ui，…，un｝为某个需要模糊决策的集合，给出了元素k种排序意见L1，L2，…，Li，…，Lk，按客观情况给出相应权重f1，f2，…，fi，…，fk，令B（x）为Li中排在x后的元素个数，其中x∈U，记

按B（x）从大到小对U中的元素进行排序，得到新的模糊综合意见。

U=｛u1，u2，…，ui，…，un｝，i=1，2，…，9。

根据表6中的实验数据，将成纱各指标进行优劣排序：

L1（条干CV值）：u1，u4，u2，u5，u7，（u3，u6，u8），u9；

L2（-50%细节）：（u1，u2），（u4，u5），u7，（u6，u8），u3，u9；

L3（＋50%粗节）：u1，u2，u4，（u3，u8），u7，u5，（u6，u9）；

L4（＋200%棉结）：u3，u6，（u2，u8），u5，u9，u7，u1，u4；

L5（条干CVb值）：u2，（u1，u4，u7），u9，u8，（u3，u5），u6；

L6（单纱断裂强度）：u1，u3，u9，u8，u2，u5，u7，u4，u6；

L7（单纱强力CV值）：u5，u9，u1，（u3，u8），u6，u7，u4，u2；

L8（毛羽指数）：u2，u3，u5，u6，u1，u9，u8，u4，u7；

L9（毛羽CV值）：u5，u4，u2，u1，u3，u8，u9，u6，u7。

计算得到9种实验方案的B（x），见表7。

表7 9种纺纱方案赛络纬纱各项测试指标的B（x）数Tab.7 B（x）of yarn property index by 9programs

根据Borda数的大小，方案1的成纱质量最好。生产80／80 210／190 67″缎纹时，该纱线的使用效果如表8所示。

4 结 语

纱线的质量评价指标体系是一个多层次、多指标的复合体系。在该体系中，各指标的相对重要性各不相同，层次分析法在专家调查问卷的基础上，通过构建层次分析模型和判断矩阵，对各指标的权重进行计算，并通过一致性检验确保权重确定的信度和效度。层次分析法的利用，降低了多指标评价体系的评价难度，提高了评价指标权重的精确性和科学性，是确定多指标评价体系权重的有效解决途径。

表8 优化后的纱线使用效果Tab.8 Property of optimized yarn

［1］ 杨锁廷.纺纱学［M］.北京：中国纺织出版社，2004.

［2］ 李隆庚.基于层次分析法的多媒体教学效果评价研究［J］.河北工业科技（Hebei Journal of Industrial Science and Technology），2007，24（4）：219-222.

［3］ 李向红，马 军.混纺比对芳砜纶／芳纶1313混纺纱成纱性能的影响［J］.河北科技大学学报（Journal of Hebei University of Science and Technology），2011，32（4）：391-395.

［4］ 许 敏，宋亚欣.基于层次分析法的知识型员工绩效考核体系设计［J］.河北科技大学学报（Journal of Hebei University of Science and Technology），2009，30（4）：365-369.

［5］ 王海燕，高 丽.基于层次分析法的中国教育公平问题研究［J］.河北科技大学学报（Journal of Hebei University of Science and Technology），2008，29（1）：72-77.