基于DV-Hop的RSSI-Hop算法
李新玲,何加铭,2
(1.宁波大学通信技术研究所,浙江宁波 315211;2.浙江省移动网应用技术重点实验室,浙江宁波 315211)
0 引言
无线传感器网络(Wireless Sensor Network,WSN)是一种全新的信息获取和处理技术,确定事件发生的位置或获取消息的节点位置是传感器网络最基本的功能之一,对传感器网络应用的有效性起着关键的作用[1]。
全球定位系统是目前应用最广泛最成熟的定位系统,具有定位精度高、实时性好以及抗干扰能力强等优点,但是GPS定位并不适用于有遮挡物存在的环境[2],节点能耗和体积较大,使用成本很高。在机器人领域中,机器人节点通常携带充足的能量供应和精确的测距设备,系统中机器人节点的数量很少,所以这些机器人定位算法不适用于传感器网络[3]。
无线传感器节点通常随机放在不同的环境中执行各种监测任务,节点的定位不依靠全局的基础设施协助定位,配置低、能量少、可靠性差,测量距离时会产生误差[4],因此定位算法必须具有较好的容错性,尽量减少节点之间的通信开销,延长网络的生存周期,并且每个节点分布式计算自身位置,而不是将所有信息传送到某个节点进行集中计算。
本文提出的RSSI-HOP算法就是一种典型的与距离无关的定位算法,通过引用节点的RSSI强度来细化节点到信标节点之间跳数,从而相对提高节点定位精度。
1 无线传感器网络节点定位方法
现有的无线传感器定位方法大致有2类:基于距离和距离无关定位[5]。基于距离定位指通过节点间测量距离或测量角度的辅助来进行节点定位的方法;距离无关定位指无需节点间的测量距离或相对角度、只依赖节点间连通信息的定位方法[6]。基于测距的方法能够为传感器提供一个精确的位置,然而,其对无线传感器网络节点的硬件要求也比较高,在一些应用领域,由于传感器节点上硬件成本和限制,通常不使用基于测距的方法[7],然而如何在低成本硬件基础上实现大范围定位的同时尽可能减少测量误差,提高定位精度是当前定位技术面临的主要困难。
1.1 距离无关定位方法
距离无关定位方法通过跳数来计算未知节点到信标节点的距离,有质心算法、APIT算法和DV-Hop定位算法。DV-Hop定位算法复杂度低,在各向同性网络中具有较高的定位精度,并且可以覆盖大范围的监测区域,网络部署成本低,目前已成为一种经典的距离无关定位方法。
1.2 DV-HOP
D.Nieulesu[8]等 人 提 出 的 APS(Adhoc Positioning system)系统采用的定位方法是:首先采用了经典的距离向量交换使所有网络节点都能获取到信标节点的以hop为单位的距离。每一个节点与其邻居节点交互更新。第2阶段,一个信标节点在与其他信标累积距离后,估计其平均每跳距离,并且将该平均单跳距离作为此信标节点的邻居节点的标准部署校正。第3阶段,任意节点在接收校正时,估计自己到信标节点的距离,以单位米表示,用于进行三边测量。其中校正值的计算方法如下:
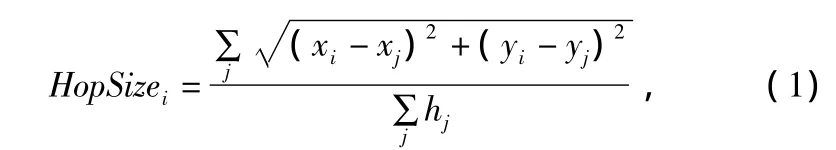
式中,(xi,yi)为第j个信标节点的位置;hj为从第j个信标节点到第i个信标节点的跳数。
如图1所示,3个信标节点A与B、B与C、C与A之间的跳数分别为7跳、4跳和4跳,测量距离分别为100 m、65 m和80 m。则估计的网络平均单跳距离为:(1065+80)/(7+4+4)=16.3 m。
1.3 RSSI
接收信号强度指示器(RSSI)是一种利用信号传递过程中强度衰减特征来进行距离估算的一种测距技术[9]。

图1 跳数信息估计网络平均单跳距离示意图

式中,PL(d)表示传播距离d之后的信号强度损耗,以dB为单位;η是耗散系数(又名信号传播常数),用于指示耗散随路径增加的速率,通常取值为2~4;d0是从发射端附近测量的一个参考距离;Xσ是随机环境噪声,遵循X~N(0)。
从RSSI的耗散模型可看出,距离越近路径耗散越小,在接收端测得RSSI值越大,距离越远,耗散越大;在接收端测得RSSI值越小,因此可以使用节点间RSSI值来作为其距离大小的比征。在此引入RSSI测距技术,仅仅作为DV-HOP算法中的一种辅助定位手段,用于限制算法中的跳数和平均每跳距离值,在算法中并不进行基于RSSI的测距。
如果一个节点与它的邻居节点之间视线连接,那么它的距离测量的平均误差非常小。如果一个节点安装在树干上、坑井中,那么它的平均误差将会非常大,因此不加选择地使用RSSI来定位野外的传感器将会产生较大的误差。
由于无线信号在空间的传播过程中随着距离的增加,信号强度不断下降,通过接收端测量信号强度的方式,就估算出发射端和接收端的距离。其理论路径耗散函数如下:
2 RSSI-Hop算法
2.1 算法改进
在实际应用中,由于地势不同,节点不均匀部署在监测区域中,导致传感器节点部署不规则,一些节点有几十个邻居节点,而一些节点只有五六个邻居节点,邻居节点之间的距离也有很大差距,最短的几米,而最长的可能有几十米。非统一部署网络中,由于标准DV-HOP算法通常会产生很大的误差,如果2个节点到相同的信标节点有相同的跳数,那么他们的位置估计将会是相同的,这明显与实际情况不符。
虽然由RSSI得到节点之间的距离有一定的测量误差,但是节点之间的RSSI随着距离的增加单调减小,仍具有参考价值。因此可以用RSSI来计算邻居节点的关于RSSI的跳数,为了表达方便,称之为RSSI跳数:

式中,∑jDrssi(i,j)表示节点到信标节点i的累积距离,Drssi(i,j)由路径耗散函数计算而得,di表示信标节点i的平均单跳距离估计:

式中,hj为从第j个信标节点到第i个信标节点的跳数。
2.2 算法模型
①信标节点向邻居节点广播自身位置数据包:{xi,yi,hopcounti,hrssii},其中(xi,yi)为信标节点 i的坐标,hopcounti为该节点到信标节点的以hop为单位的最短距离,hrssii为该节点到信标节点RSSI跳数,计算方法如式(3)所示。其中di是根据信标节点之间RSSI累积距离计算出来的平均单跳距离,由此得到的Hrssi节点间跳数信息作为参考,计算节点到信标节点之间的距离。根据RSSI距离在节点短距离视线靠近时接近真实距离,具有很高的参考价值。相反的,节点间距离较远或有遮挡物时,RSSI距离较大,相应的距离信息也不准确,不具有参考价值,因此该处节点到信标节点跳数计算公式如下:
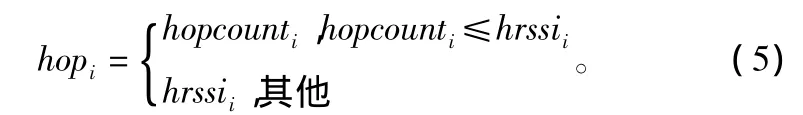
②计算该节点到信标节点i的距离ri,计算公式如下:
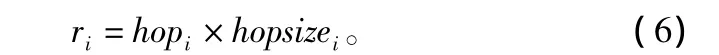
③当该节点与大于等于3个信标节点有距离估计时,利用三边测量法估算出自身位置,并升级为附加信标节点参与后续迭代定位过程,辅助剩余节点定位。
3 仿真实验
3.1 实验设计
本文的实验在OMNET平台上进行,采用c++编程,节点分为信标节点和普通节点,hop by hop方式进行节点信息交互,估算节点到信标节点位置,为了监测本算法的性能,同时客观获取实验结果数据,实验数据由多次实验获取统计数据的平均值计算而得,所有节点均采取而为随机部署方式进行部署。
3.2 实验结果分析
在仿真中,节点随机部署在500 m*500 m的方形区域中,设置节点的通信距离为30 m。信标节点个数为6,节点密度为6。选取其中100个节点的定位结果,比较结果如图2所示。因为无线线路中的RSSI是非常不稳定的,并且对环境因素十分敏感,很难建模,因此在仿真时随机选取50%的节点分布不均匀,且其平均相对测量误差为20%。其余节点对之间的测量误差较小。误差较大的节点所占比例越多,表明网络节点部署越不均匀,DV-hop中以跳数表示的节点到信标节点的距离也就也失真。
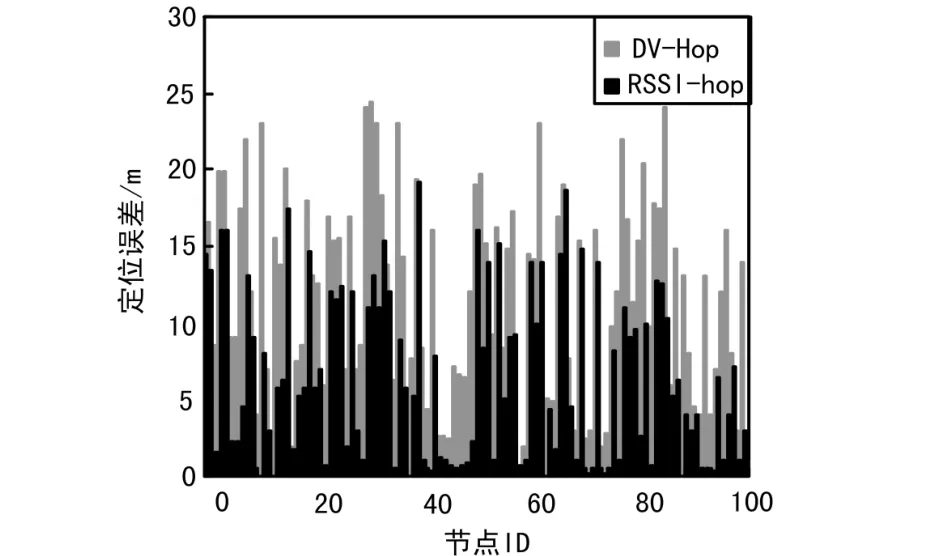
图2 定位结果比较
如图2所示,RSSI-Hop的定位误差明显减小,这表明,虽然由RSSI得到的距离估计存在一定的误差,但是其在一定程度上仍能在一定程度上反映出节点分布状况,由此得到的节点到信标节点的跳段距离更接近于真实距离。尤其当节点分布较为密集时,节点对越接近,由RSSI得到距离值越接近真实距离,得到的hop数就越真实。

图3 定位结果比较
当节点密度较低时,DV-Hop性能较差,这是因为节点不统一分布状况明显,跳数所表示的距离严重偏离真实值;当节点密度较大时,这一问题得到缓解,定位精度因此也提高了,尤其是节点密度由3增加到10时,平均误差明显下降。RSSI-Hop随节点密度增加,Drssi(i,j)的相对误差降低,由Hrssi(i)表示的距离更接近真实值,因此定位精度也随之提高。当节点密度增加到一定程度之后,由于受到网络中信标节点数量等因素的制约,节点平均定位误差不再下降而是趋于平和。
4 结束语
通过分析经典的DV-Hop定位算法在计算节点到信标节点跳段距离的方面的不足,提出根据RSSI耗散模型的距离相关特性,引入Hrssi辅助估算各节点到信标节点之间的跳段距离,实验证明该算法有效提高了网络中节点密度较大区域节点定位精度,减少了由于节点到信标节点跳段距离相同而引起的定位冲突,提高了迭代效率,具有良好的定位效果。但是在障碍物大量存在的网络,RSSI并不能很好地反应距离相关特性,不能明显提高定位精度。
[1]TRIGONI N,KRISHNAMACHARI B.Sensor Network Algorithms and Applications[J].Phil.Trans.Roy.Soc,2012(370):5-10.
[2]SCHMID J,BEUTLER F,NOACK B,et al.An Experimental Evaluation of Position Estimation Methods for Person Localization in Wireless Sensor Networks[J].Lecture Notes in Computer Science,2011(6567):147-162.
[3]孙利民.无线传感网络[M].北京:清华大学出版社,2005:148-155.
[4]AMUNDSON I,SALLAI J ,KOUTSOUKOS X,et al.RF Angle of Arrival-based Node Localisation[J].International Journal of Sensor Networks,2011(9):209-224.
[5]COTARUIZ J,ROSILES J,ERNESTO S,et al.A Low-Complexity Geometric Bilateration Method for Localization in Wireless Sensor Networks and Its Comparison with Least-SquaresMethods [J].Sensors,2012(12):839-862.
[6]BOUKERCHE A,OLIVERIA H A B F,NAKAMURA E F,et al.Secure Localization Algorithms for Wireless Sensor Networks[J].Communications Magazine,IEEE,2008(46):96-101.
[7]STANKOVIC J A,TIAN He.Energy Management in Sensor Networks[J].Phil.Trans.Roy.Soc,2012(370):52-67.
[8]NICULESCU D,NATH B.DV Based Positioning in ad hoc Networks[J].Journal of Telecommunication Systems,2003,22(1):267-280.
[9]WEI Xi,HE Yuan,LIU Yun-hao,et al.Locating Sensors in the Wild:Pursuit of Ranging Quality[C]∥New York:Proceedings of the 8th ACM Conference on Embedded Networked Sensor Systems,2011:295-308.

