鱼雷浅水主动声引信的一种布阵方法

崔户山，王明洲，白志科，张文波

(1.中国船舶重工集团公司第七〇五研究所，陕西 西安 710075;2.水下信息与控制重点实验室，陕西 西安 710075)

0 引言

鱼雷作为重要的水下攻击武器，既能攻击水下目标，又能打击水面舰艇。而水声技术的研究，主要是对目标进行探测、估计、跟踪和定位。半个多世纪以来，随着人们对水下声学环境认知的不断深入，微电子和信号处理等技术的飞速发展，以及应用需求等多方面的推动，水声技术得到迅猛发展。近年来，对水下高速目标的探测、认知和定位日益受到重视，成为水声技术的一个重要研究领域。

在浅水状态下，鱼雷主动声引信应用较少，主要有2方面原因:一是主动声引信在水下环境中工作时，存在的干扰主要有海洋环境噪声、混响和运动目标的航行辐射噪声。除海洋环境噪声外，其他2种都是强干扰背景。尤其在浅水状态下混响强，信混比较低，一般条件下检测概率低。二是主动声引信发送窄脉冲，频率分辨率低，信号检测困难。在国外声引信鱼雷多用于深水反潜，由于在深水状态下界面混响影响小，信混比较高，检测成功率高，相对可靠。在浅水采用声引信具有一定的技术难度。本文通过提高引信发射信号频率，利用接收动目标回波信号的多普勒特性，提出一种适合浅水声引信的布阵形式，并给出了初步的设计参数和计算结果。

1 指向性函数

指向性函数［1］是描述发射阵辐射声场(自由远场)或接收阵灵敏度的空间分布函数，指向性函数也称作指向性图、方向特性函数等。

采用左手坐标系来绘制和测量阵的指向性图。

图1 左手坐标系Fig.1 Reference frame of left hand

1.1 N个点源任意分布的离散阵的指向性函数

如图2所示，各阵元的位置由矢径ri=(xi，yi，zi)表示。在(α，θ)方向，入射声线的单位矢量为e=exi+eyj+ezk，其中 ex=sinθcosα，ey=sinθsinα，ez=cosθ。如若采用相控技术使主波束在 (α0，θ0)方向上，设该方向上的单位矢量为m=mxi+myj+mzk，其中 mx=sinθ0cosα0，my=sinθ0sinα0，mz=cosθ0。

图2 任意分布离散阵的坐标系Fig.2 Reference frame of discrete arrays

取坐标原点o为参考点，则沿任意方向(α，θ)入射的声线使第i号阵元相对参考点o的声程差ξi=ri·e=xiex+yiey+ziez。来自主极大方向的声线使第i号阵元相对参考点o的声程差ξi0=ximx+yimy+zimz。因此任意方向(α，θ)入射的声波使第i号阵元相对主极大方向(α0，θ0)入射的声波的相位差为

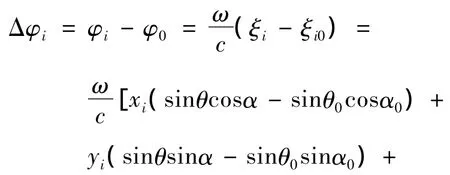
其中，c为声速;ω为工作角频率。N个阵元任意分布的离散阵在三维空间的指向性函数为

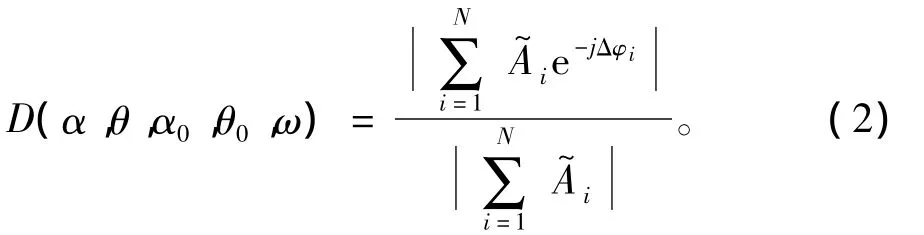
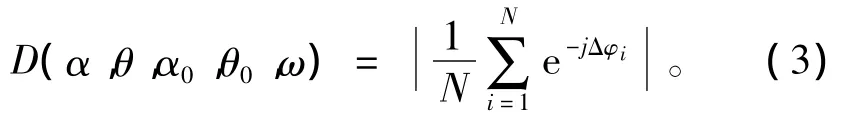
1.2 连续体的指向性函数

有连续曲面阵的指向性函数为

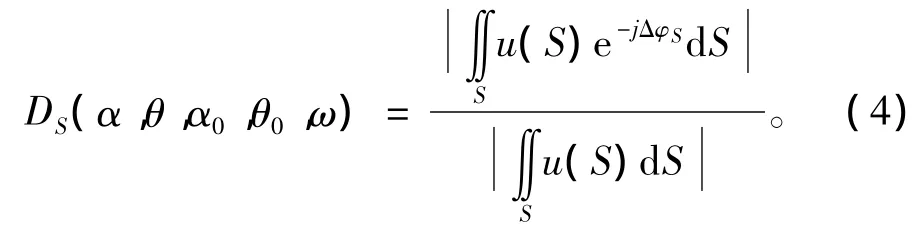
式中:u(S)为连续面上的响应分布函数，也称做孔径分布函数;ΔφS为连续体各积分元在(α，θ)方向的声波相对于主极大(α0，θ0)方向的声波的相位差。

将矩形阵置于oyz平面上，设y和z轴所对应的矩阵的两边长为b和a。坐标原点在矩形活塞阵的对称中心。面元dS相对于对称中心o的相位差为

将上式代入式(4)，被积函数u(S)为常数，于是其指向性函数为

取定向面为面 oxz，即 α =0°，0°≤θ≤180°。则有

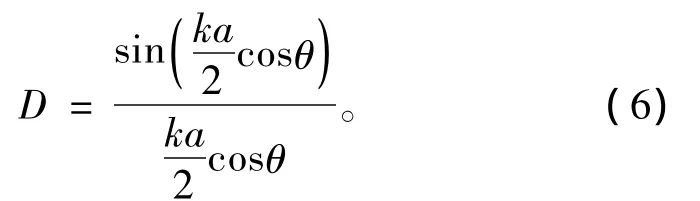
2 布阵方法

2.1 前向－周向布阵方法

如图3所示，矩形阵元A布在雷头前端面，将矩形阵元B放置在侧面上。如图4所示，在雷头对称的排列出3～4对阵元。令矩形阵元A的一边为a，矩形阵元B的两边分别为c和d。

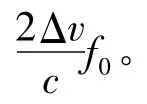
对矩形阵元A，为在频率f0时波束宽度达到要求(θ－3dB≥90°)，计算得出 a边长最大为6.2 mm。

对矩形阵元B波束宽度要求为θ－3dB≥60°，结果见表1。

表1 矩形阵元B尺寸参数Tab.1 Size parameter of array B

表1中c和d长度均为满足条件时的最大长度。

通过分析可看到，前向－周向布阵方法中的B阵元角度利用不够充分，会造成引信覆盖的盲区。

2.2 前向－侧周向布阵方法

如图5所示，前向－侧周向布阵方法与前向－周向布阵方法的区别是将矩形阵元B放置在雷头的斜面上，波束宽度要求有所不同，计算方法与前向－周向布阵方法一致，由其波束宽度确定各个阵列的尺寸大小。

图5 前向－侧周向布阵示意图Fig.5 Arrays in front-side around direction

为实现引信角度的全覆盖，在临界条件下，各个角度之间有如下关系:

为确定最合适角度，综合考虑，下列角度选择较为合适，即当α =65°，β=50°时，矩阵A的频率为f0，a边覆盖角度θ－3dB≥50°，可得a边长最大为10.5 mm，θ－3dB=50°。此时a边对应的波束图如图6所示。

图6 a边对应波束图Fig.6 Beam pattern of side a

在径向布放4对换能器，频率及尺寸的最大值在表2中给出。

表2 矩形阵元B尺寸参数Tab.2 Size parameter of array B

采用前向－侧周向布阵方法，各个阵元尺寸较为适中，且阵元尺寸符合要求。

3 换能器厚度计算

根据厚度计算公式，即

当工作频率等于长棒固有的基波特征频率时，机械振动系统达到谐振，即当工作在谐振时，棒长应等于工作频率时声波波长的二分之一。选用PZT－4型压电陶瓷，故有如下计算:

则根据式(8)，可计算出各个频率矩形阵元所对应的厚度。

4 目标的多普勒频移

如图7所示，鱼雷在行进过程中，目标在波束覆盖的范围内出现。2种极限情况是:目标速度方向和鱼雷速度方向相反、目标速度方向和鱼雷速度方向垂直。在这2种极限情况下，可求得目标对于鱼雷位置角度η与θ、目标速度方向角度φ与δ角度变化时的多普勒频移，如图7所示。其中鱼雷速度v为40 kn，目标速度v1为20 kn。

图7 鱼雷检测目标角度示意图Fig.7 Angles when detecting target

图7中，φ和δ分别为目标速度方向与水平方向、垂直方向的夹角;η为目标与矩形阵元A几何中心的连线与矩形阵元A法线的夹角，θ为目标与矩形阵元B几何中心的连线与垂直方向的夹角。则对矩形阵元A，有

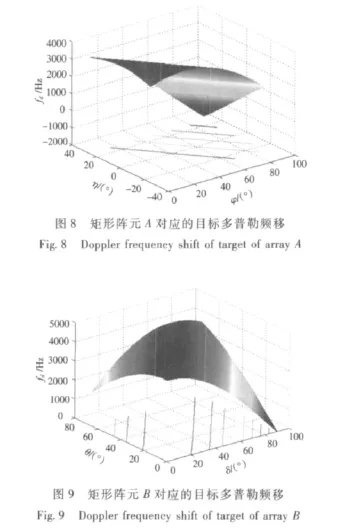
其中，η的变化范围为［－25°，25°］;φ的变化范围为［0°，90°］。故可得矩形阵元A对于目标的多普勒频移三维图如图8所示。

对矩形阵元B，有

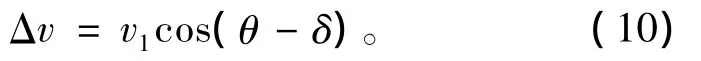
其中，θ的变化范围为［0°，65°］;δ的变化范围为［0°，90°］。可得矩形阵元B(以f1为例)对于目标的多普勒频移三维图如图9所示。

综上所述可得如下结论:

1)若采用时宽为1 ms的信号，频谱宽度约为1 kHz，则对矩形阵元A检测模糊区为

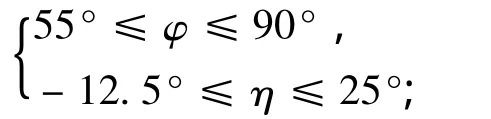
对矩形阵元B(以f1为例)检测模糊区为

2)若采用时宽为2 ms的信号，频谱宽度约为500 Hz，则对矩形阵元A检测模糊区为

对矩形阵元B(以f1为例)检测模糊区为

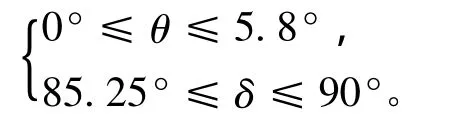
5 结语

本文设计了浅水状态下的主动声引信模型，给出了引信各个部分的尺寸计算方法，获得了各个矩阵对应的多普勒频移图，针对频移图来确定目标。本文确定了一种有效的布阵方案，是在浅水状态下对抗混响的一种有效方式，是对浅水主动声引信研究的一次积极的探索。

［1］栾桂冬，张金铎，王仁乾.压电换能器和换能器阵［M］.北京:北京大学出版社，2005.

［2］周福洪.水声换能器及基阵［M］.北京:国防工业出版社，1983.

［3］杨崇林，陆善明，姚蓝.水下动目标近程主动声引信技术研究［J］.中国造船，2000，41(4):79 －84.YANG Chong-lin，LU Shan-ming，YAO Lan.Study and implementation of active acoustic fuze for underwater moving target［J］.Shipbuilding of China，2000，41(4):79－84.

［4］R.J.尤立克.水声原理［M］.洪申，译.哈尔滨:哈尔滨船舶工程学院出版社，1990.

［5］ETTER P C.水声建模与仿真［M］.蔡志明，等译.北京:电子工业出版社.

［6］HINES P C，ELLIS D D.High-frequency reverberation in shallow water［J］.IEEE Journal of Oceanic Engineering，1997，22(2):292 －298.